各国规范中长柱二阶效应的比较

夏少华

(深圳市市政设计研究院有限公司，广东深圳 518029)

0 引言

钢筋混凝土受压柱在偏心荷载作用下将发生纵向弯曲，即产生侧向挠度f，侧向挠度f将引起附加弯矩Mf。以两端铰接的长柱来说明，初始偏心距M0，压力N，构件上的弯矩由初始弯矩（一阶弯矩）M1=Ne0和由横向挠度f引起的附加弯矩（二阶弯矩）M2=Mf之和组成。即 M=M1+M2=M（e0+f），取 η＝，用η反映因二阶弯矩影响承载力低的效应。η值越大，表明二阶弯矩影响愈大，一阶弯矩在总弯矩中所占的比例愈小，所以计算η值的实质就是在计算横向挠度f。

《公路钢筋混凝土及预应力混凝土桥涵设计规范》JTG-D62-2004[1]中的η计算公式是基本长柱作为研究对象，并假定柱单向弯曲,以构件最大变形fmax产生的附加弯矩和外荷载直接相加。可见，η是对控制截面而言。对于构件的其他截面，如果均以fmax处算得的η值来设计，则易造成构件配筋量冗余多大，过于保守。在抗震鉴定中会以为柱的强度不足需要加固的后果。研究表明，长柱有无侧移时二阶效应是有区别的，本文针对各国规范规定的二阶效应公式进行探讨。

1 二阶效应

在竖向荷载和弯矩作用下，结构构件发生挠曲变形，施加于构件上的轴力又在挠曲变形的基础上产生附加弯矩，这种附加弯矩称为二次弯矩，这种现象称为二阶效应。如图1所示，在初始偏心距为e的荷载N作用下产生纵向弯曲变形，即侧向挠度f，Ne为构件的一阶弯矩，Nf即为轴力在侧向挠度上引起的附加弯矩或二阶弯矩。当构件的长细比较大时，纵向弯曲的影响不容忽视，计算中必须考虑轴力在侧向挠度上产生的附加弯矩对构件承载力的影响，否则会影响结构的安全。

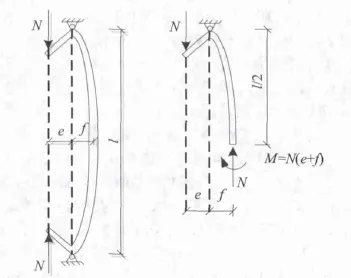
图1 结构构件的二阶效应

在荷载作用下，结构整体的变形分为构件的变形和结构的变形。构件变形引起的弯矩增大称为P-δ效应，整体结构变形引起的弯矩增大称为P-Δ效应。当结构的侧向刚度很大或侧向变形受到约束时，水平荷载下的P-Δ效应产生的附加内力很小，结构可视为无侧移，即为无侧移结构(见图2(a))；如果结构的侧向刚度不大或侧向变形不受约束，竖向荷载全部作用在节点上，这时需考虑柱在竖向荷载下的P-δ效应及整个结构在水平荷载和竖向荷载下的P-Δ效应，即为有侧移结构(见图2(b))。美国规范ACI 318-08认为，如果由二阶效应产生的柱端部弯矩增大不超过一阶弯矩的5%，则认为柱是无侧移的。由于无侧移结构和有侧移结构产生的附加变形和附加弯矩不同，设计中需区分两种情况。

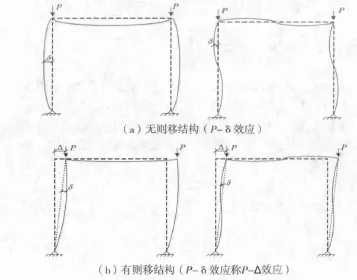
图2 无侧移结构和有侧移结构

对于有侧移结构偏心受压构件二阶效应附加弯矩的计算，目前已形成了计算机分析方法和实用简化方法等多种方法。现有的方法大致分为4类：杆系结构考虑二阶效应的非线性有限元法、考虑二阶效应的结构弹性有限元法、计算有侧移结构二阶效应附加内力的各种弹性简化方法(包括迭代P-Δ法、层增大系数法、结构整体增大系数法、负刚度杆件法和负面积杆件法等，其中以层增大系数法最为普遍)以及使用柱截面偏心距增大系数(或弯矩增大系数)的方法。

我国梁规JTG-D62-2004[1]采用截面偏心距增大系数法,我国建筑规范GB50010—2010[2]采用弯矩增大系数法；美国建筑规范ACI 318-08[3]采用非线性二阶分析和弯矩增大法，美国桥梁规范AASHTO LRFD 2007[4]采用弯矩增大法；欧洲规范EN1992-1-1:2004[5]采用基于非线性二阶分析的一般方法、基于名义刚度的二阶分析和基于曲率的方法计算构件的二阶效应。

1.1 中国建筑规范

中国建筑规范GB 50010-2010采用弯矩增大系数法考虑构件的二阶效应，偏心受压构件考虑轴力在挠曲构件中产生的二阶效应后，控制截面的弯矩设计值按式(1)计算：

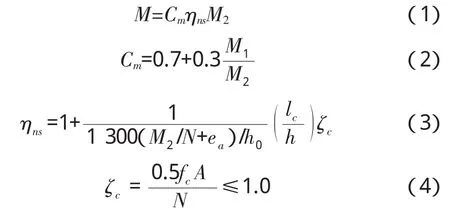
式中：Cm——为构件截面偏心距调节系数，当小于0.7时取0.7；

ηns——弯矩增大系数，当Cmηns小于1.0时取1.0；

N——与弯矩设计值M2相应的轴力设计值；

ea——附加偏心距，其值取20 mm和偏心方向截面最大尺寸1/30两者中的最大值；

ζc——截面曲率修正系数，当计算值大于1.0时取1.0；

h——构件截面高度；

h0——构件截面有效高度；

A——构件截面面积；

lc——构件计算长度。

1.2 中国桥梁规范

中国桥梁规范JTG-D62采用偏心距增大系数计算构件的二阶效应：

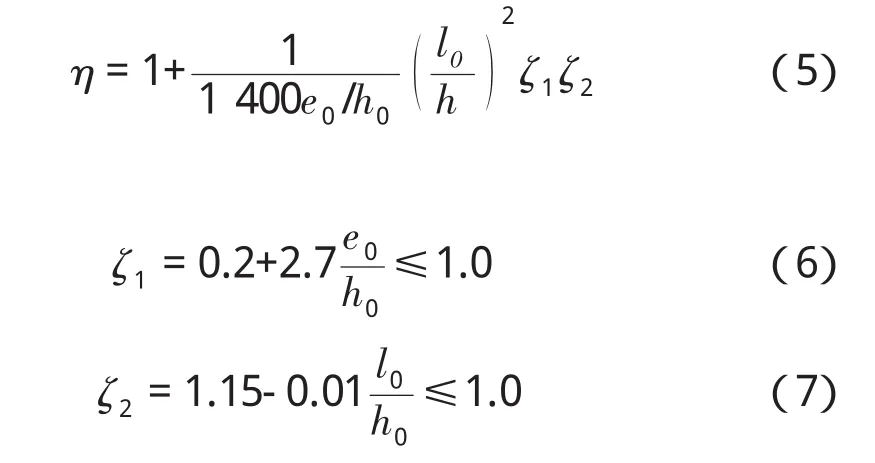
式中：l0——构件的计算长度；

e0——轴力对构件截面重心轴的偏心距；

h0——构件截面有效高度；

h——构件截面高度；

ζ1——荷载偏心率对构件截面曲率的影响系数；

ζ2——构件长细比对构件截面曲率的影响系数。

1.3 美国建筑规范

美国建筑规范ACI 318-08计算构件的二阶效应时区分了无侧移结构和有侧移结构。

1.3.1 无侧移框架

美国建筑规范ACI 318-08采用弯矩增大系数法计算无侧移结构构件的二阶效应。受压构件二阶弯矩的计算公式为

其中

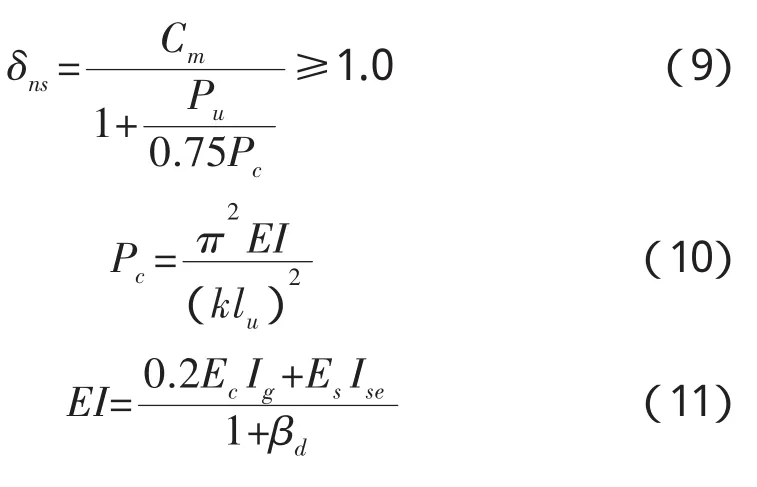
或

式中：Mc——考虑二阶效应的增大弯矩；

M2——受压构件较大的乘系数（荷载系数）的端部弯矩，恒为正且不小于M2,min=Pu（0.6+0.3h）；

δns——无侧移框架的弯矩增大系数；

Pu——给定偏心距时乘系数的轴向荷载；

Ig——不考虑钢筋的混凝土构件毛截面对重心轴的惯性矩；

Ise——钢筋对构件截面重心轴的惯性矩；

βd——最大乘系数的轴向持续荷载与相同荷载组合中最大乘系数的轴向荷载之比；

Cm——实际弯矩图等效为均布弯矩图的等效系数，对于支座间有横向荷载的构件，Cm取1.0，对于支座间无横向荷载的构件，按式(13)计算；对于M2,min大于M2的构件，Cm取为1.0或按M1/M2计算：

1.3.2 有侧移框架

美国建筑规范ACI318-08规定，对于有侧移框架，分别按式(14)和式(15)计算端部弯矩：

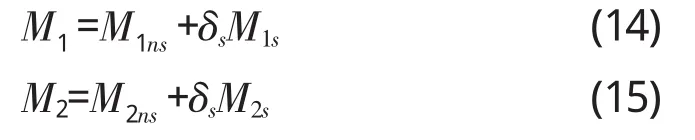
式中：M1——受压构件较小的乘系数的端部弯矩，构件单曲率弯曲时为正，双曲率弯曲时为负；

M2——受压构件较大的乘系数的端部弯矩，恒为正；

M1ns、M2ns——无显著侧向荷载作用下，用一次弹性框架分析方法计算的构件在M1、M2作用下乘系数的端部弯矩；

M1s、M2s——有显著侧向荷载作用下，用一次弹性方法计算的构件在M1、M2作用下乘系数的端部弯矩；

δsM2——二阶弯矩；

δs——弯矩增大系数，按式（16）计算：

ΣPu、Vu——楼层中的竖向总荷载和楼层剪力；

Δ0——按Vu确定的楼层顶部与底部的一阶相对位移；

lc——楼层层间高度。

若式(16)计算的δs大于1.5，则应按二阶弹性分析或式(17)计算 δs：

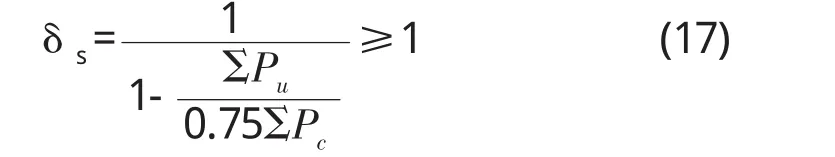
式中：ΣPu——某层所有乘系数竖向荷载之和；

ΣPc——某层所有无侧移柱荷载之和，Pc按式（10）计算。

1.4 美国桥梁规范

美国桥梁规范AASHTO LRFD-2007用弯矩增大系数法计算构件的二阶效应：

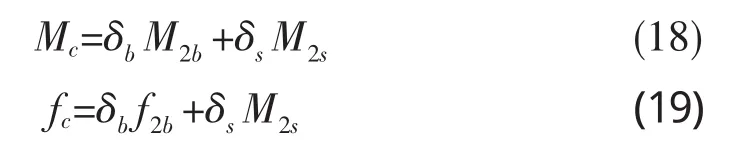
其中

式中：M2b——受压构件由不产生较大侧移的乘系数重力荷载引起的弯矩，恒为正；

M2s——受压构件由产生侧移Δ（大于lu/1 500）的乘系数的侧向或重力荷载引起的弯矩，恒为正，Δ由常规的一阶弹性分析计算；

f2b——相应于M2b的应力；

f2——相应于M2s的应力；

Pu——乘系数的轴向荷载；

φK——刚度折减系数，对混凝土构件，φK=0.75；

Pe——欧拉压屈荷载，同式(10)。

对于无侧移结构构件，无特殊规定时δs取1.0。对于有侧移结构构件，δb按无侧移结构构件确定，δs按有侧移结构构件确定。

对于无侧移且无横向荷载结构的构件，Cm按式(22)计算：

式中：M1、M2——较小、较大的端部弯矩。

如果构件为单曲率弯曲，则M1/M2为正；否则为负。对于其他情况，Cm取1.0。

1.5 欧洲规范

欧洲规范考虑二阶效应的分析方法包括基于非线性二阶分析的一般方法、基于名义刚度分析方法和基于名义曲率的分析方法。下面介绍基于名义刚度法(可用于独立构件和整体结构)和基于名义曲率法(主要适用于独立构件，如果采用合理的曲率分布假定，也可用于整体结构)。

1.5.1 基于名义刚度法

在基于名义刚度的分析方法中，细长受压构件的刚度按名义刚度计算，即：

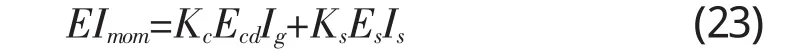
式中：Imom——名义惯性矩；

Ecd——混凝土弹性模量设计值

γcE——混凝土弹性模量分项系数，建议值为1.2；

Ig——混凝土截面惯性矩；

Is——钢筋面积对混凝土面积中心的惯性矩，

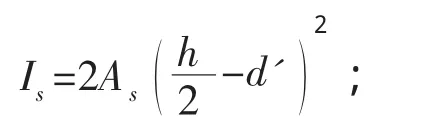
h——构件截面高度；

d'——钢筋中心到构件最近表面的距离；

Kc——考虑裂缝、徐变等的影响系数；

Ks——钢筋影响系数，当配筋率时P≥0.002，取

φef——有效徐变率；

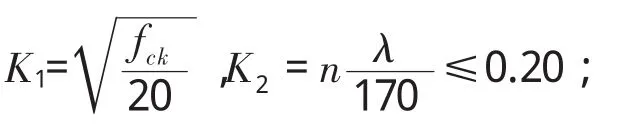
n——轴压比；

i——受压构件的截面回转半径。

构件截面弯矩M按式（24）计算：

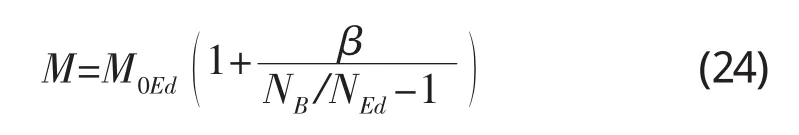
式中：M0Ed——一阶相对弯矩，当一阶杆端相对弯矩M1和M2不等时(M2>M1)，可用等效的一阶端部弯矩M0e代替，即

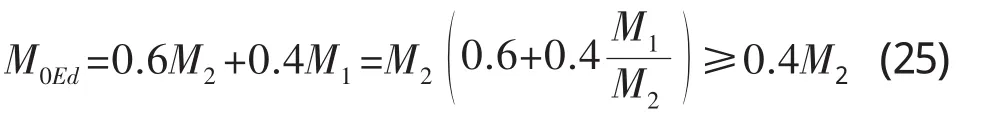
β——与一阶弯矩和二阶弯矩分布有关的系数，对于轴向荷载和截面不变的独立构件，假定二阶弯矩为正弦分布，则有

c0——依赖于一阶弯矩分布的系数，一阶弯矩为常数时c0=8，抛物线分布时c0=9.6；对称三角形分布时c0=12；

NEd——轴向荷载设计值；

NB——按名义刚度计算的压屈荷载

1.6 二阶效应计算方法对比

在上面的各国混凝土规范中，我国建筑规范和我国桥梁规范的公式不区分无侧移结构和有侧移结构(实际公式是针对无侧移结构的)，我国建筑规范同时引入了调整参数Cm，我国桥梁规范没有考虑构件两端弯矩不相等情况的调整。美国建筑规范区分了无侧移结构和有侧移结构，两种情况附加弯矩的计算方法有一定区别，同时考虑了构件两端弯矩不相等情况的调整。美国桥梁规范的计算公式同时考虑了无侧移和有侧移两种情况。欧洲规范没有明确无侧移结构和有侧移结构，但计算二阶效应时考虑的影响因素比较细致。

2 结语

（1）二阶效应的计算方法分为基于刚度的计算方法和基于曲率的计算方法。基于刚度计算方法是考虑构件开裂后刚度的降低对构件的刚度进行折减，按弹性方法分析；基于曲率计算方法是直接按弹塑性方法进行分析的。我国建筑规范和我国桥梁规范采用基于曲率的计算方法，美国建筑规范和美国桥梁规范采用基于刚度的计算方法，欧洲规范同时提供了两种方法。由于各规范公式考虑的因素及参数取值不同，在相同的条件下，二阶效应计算有时差别很大。

（2）各国规范中，美国建筑规范、美国桥梁规范和欧洲规范给出了二阶效应的确定方法。无侧移结构和有侧移结构的二阶效应不同，我国建筑规范和我国桥梁规范没有进行区分，美国建筑规范和美国桥梁规范、欧洲规范对两种结构进行了区分。为精细化设计，建议规范应细化二阶效应计算公式。

[1]JTG D62-2004,公路钢筋混凝土及预应力混凝土桥涵设计规范[S].2004.

[2]GB 50010-2010,混凝土结构设计规范[S].2011.

[3]ACI318-08,Building code requirements for structural concrete and commentary[S].American Concrete Institute,2008.

[4]AASHTOLRFDBridge Design Specifications[S].American Association of State Highway and Transportation Officials,2007.

[5]EN 1992-1-1:2004,Design of Concrete Structures.General Rules and Rules for Building[S].CEN,2004.