神舟十号中的摆球机械能守恒吗

唐建勋

（无锡市辅仁高级中学，江苏 无锡 214123）

北京时间2013年6月20日上午10点，神舟十号航天员王亚平在太空为地面学生进行了太空授课，实施在轨讲解和实验演示，并与地面师生进行双向互动交流.王亚平在授课过程中演示了摆球运动实验，如图1所示，固定支架上用细绳连接一个小球，用手指轻推小球，给小球一个初速度，小球开始绕着支架的轴心不停地做匀速圆周运动.该实验展示了在太空失重环境下，具有初速度的小球在细绳拉力下的运动情况.

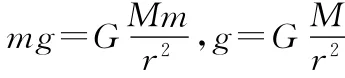
图1

但当笔者解释完小球完全失重的原因时，却有学生提出了一个很独特问题：小球如果真的受到重力，还能做匀速圆周运动，那岂不是小球机械能不守恒了？因为小球做匀速圆周运动时，动能不发生改变，而小球的高度却发生了变化，所以小球的机械能在变化，机械能不守恒！这个问题的提出，引发了课堂上的激烈争论，另一学生立刻反驳：小球在获得了手指推动的初速度后，除了重力外，并没有外界其他力对小球做功，机械能应该守恒！双方似乎都有道理，前者从机械能的定义判断摆球的机械能在发生改变，而后者从机械能守恒的条件入手，得到小球机械能守恒，问题陷入了僵局.在普通高中人教版教材中，机械能守恒定律的表述为：在只有重力或弹力做功的物体系统内，动能与势能可以相互转化，而总的机械能保持不变.在大学普通物理学教程《力学》中，机械能守恒定律研究的对象升级为质点系，其表述为：在一过程中，若外力不做功，又每一对内非保守力不做功，则质点系机械能守恒.不难发现，无论是按照高中还是按照大学教材的定义，神十中的小球只受重力与拉力，拉力不做功，而重力是保守力，其做功不影响机械能守恒，所以小球的机械能应该守恒.但是我们明明又观察到小球的动能不变，重力不能忽略不计，因此重力势能在不断变化，所以总的机械能的确在发生变化而不守恒.为什么这其中的理论与现象会有如此矛盾的结果呢？

其实无论是高中抑或是大学教材，在论及动能定理、功能关系、机械能守恒问题时，都是从力做功开始的，它们所涉及力学问题的阐述都遵从牛顿运动定律，但是牛顿运动定律却非适用于所有情况.例如非惯性系.高中或大学在讨论机械能守恒时，都有一个共同的默认前提，就是所选择的参考系为惯性系，因为只有在惯性系中牛顿运动定律才是成立的.以惯性系为基础的理论体系下的机械能守恒定律的表述就应如教材所示：外力不做功，同时内非保守力所做总功为0，则质点系机械能守恒.然而在非惯性系下，牛顿运动定律不再适用，那么机械能守恒这一问题会变得如何呢？具体可以分以下3种情况讨论.

1 相对惯性系做匀变速直线运动的非惯性系

在做匀变速直线运动的非惯性系中，质点运动不再符合牛顿第一定律.因为质点即使不受任何力，也会产生一个与非惯性系自身加速度a等大反向的加速度－a，所以可以认为质点在非惯性系中受到一惯性力f，它的方向与非惯性系的加速度方向相反，大小等于质点的质量m与非惯性系加速度a的乘积，即f＝－ma.在此情况下，惯性力会对质点系做功W，那么这个额外的功会改变质点系的机械能吗？

首先有必要了解一下势能的定义：某位置的势能等于从势能零点到此位置保守力所做功的负值，由此可见势能是在保守力概念的基础上提出的.而保守力又是这样定义的：若一个力所做的功仅由受力质点初末位置决定而与质点所经历的路径无关，这种力就叫做保守力.可以证明，在地球表面附近质点所受重力、在匀强电场中点电荷所受静电力、在一固定电荷附近的点电荷所受库仑力、与弹簧相连的质点所受弹力等等，这些力做功均与路径无关，仅与质点或点电荷的初末位置有关，这样的力都是保守力，相应的，也就衍生出了重力势能、电势能、弹性势能等概念.那么做匀变速直线运动的非惯性系中的惯性力是什么力呢？由于相对惯性系做匀变速直线运动的非惯性系的加速度恒定，惯性力f为定值，所以惯性力对质点做功为Wf＝f·x＝fxcosα＝－ma·xcosα＝－mal.可以发现惯性力做功仅与位移大小x和加速度方向与位移方向夹角α有关，与路径无关，说明惯性力是保守力.惯性力是保守力，必定伴随产生一个势能，其表达式可由势能定义得Ep惯＝mal，其中l为质点到零势能面的距离，我们可以把Ep惯称为惯性力势能.

2 相对惯性系做匀速转动的非惯性系

如果一个参考系相对于惯性系匀速转动，其中的质点若要与匀速转动的参考系保持相对静止必须始终受一个指向转动轴心的向心力.质点受一个外力（向心力）却能保持静止，对此参考系来说这同样不符合牛顿运动定律，因此这样的参考系也是非惯性系.在此非惯性系中为了保持牛顿运动定律形式不变，也必须要引入一个力，该力方向与指向转动轴心的向心力相反，大小与向心力相等，即f＝mω2r.若质点在该非惯性系中不受其它外力，它将会在这个力的作用下远离轴心，所以这个力被称为离心惯性力.那么这个力的存在又会对质点的机械能造成什么影响呢？

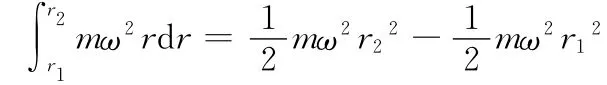
3 质点相对匀速转动的非惯性系运动

由大学普通物理学可知，若质点相对于匀速转动的非惯性系运动，还要受到科里奥利力，其表达式为f科＝2m×ω.由表达式可以发现，科里奥利力方向始终与速度方向垂直，这意味着科里奥利力对质点始终不做功.

在了解了非惯性系中各种额外力的做功情况后，我们重新来审视质点系的机械能守恒问题.在惯性系中的质点系机械能守恒条件是除了内保守力外，其它力不做功或所做总功为0，其原因就在于内保守力做功时，机械能没有流出或流入质点系.因为从做功的本质来说，它是能量转化的量度，内保守力做功其实是质点系机械能内部不同能量形式之间的转化，这是不影响机械能总量的，而其它力不得做功，因为这也会转化能量，但这是质点系机械能以外的能量与质点系机械能之间的转化，这就破坏了质点系的机械能守恒.如果从这个意义上说，非惯性系内由于存在惯性力做功，所以机械能似乎是不守恒的.但是惯性力与离心惯性力都是保守力，它们都对应有相关的势能，惯性力对应的是惯性力势能Ep惯，离心惯性力对应的是离心惯性力势能Ep离，我们可以将上述两种势能合并成为非惯性系中的总惯性力势能Ep惯总，其中Ep惯总＝Ep惯＋Ep离.再把这个总惯性力势能与质点系的动能、重力势能、弹性势能的总和定义为机械能，那我们就能得到新的非惯性系下的机械能守恒定律：在以匀加速平动与匀速定轴转动为合运动的非惯性系中，除内保守力、惯性力、离心惯性力做功外，其它力不做功或所做总功为0，则质点系机械能守恒，表达式 为Ek＋Ep＋Ep弹＋Ep惯总＝Ek′＋Ep′＋Ep弹′＋Ep惯总′.其中Ek为质点系总动能，Ep为质点系总重力势能，Ep弹为质点系总弹性势能，Ep惯总为质点系总惯性力势能.

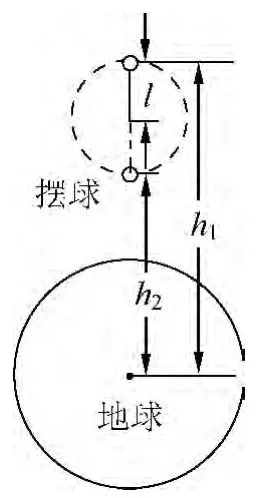
图2

在认识了非惯性系下的机械能守恒定律之后，我们就能解决神州十号中摆球的机械能是否守恒的问题了.从非惯性系机械能守恒定律的条件来看，小球受摆绳拉力、重力、离心惯性力、科里奥利力，其中摆绳拉力和科里奥利力方向始终垂直于速度方向，所以都不做功，而重力与离心惯性力在做功，但不影响机械能守恒，所以小球的机械能应当守恒.但之前有学生认为小球机械能不守恒，理由是小球做匀速圆周运动时，动能不发生改变，而小球的高度却发生了变化，重力势能在变化，所以小球的机械能在变化.现在从非惯性系下的机械能守恒定律来看，这种说法不完整的，因为在研究小球的运动时，我们是以绕地心为轴心的匀速转动的非惯性系为参考系的，所以小球除了动能与重力势能外，还应包括总惯性力势能.由于该参考系没有匀加速直线运动的平动加速度，但是有绕地心匀速转动的角速度，所以没有惯性力势能，而有离心惯性力势能，在分析小球机械能的时候就必须要考虑它的离心惯性力势能.摆球在神十内做圆周运动时，设摆绳长度为l，它从最高点运动至最低点的过程中摆球重力势能减少2mgl（其中g为该轨道高度处重力加速度），设摆球在以地心为圆心的转动参考系中的最高最低两位置的轨道半径分别为h1、h2，如图2所示.由摆球离心惯性力势能表达式可得其增量为

可以发现摆球下落过程中重力势能的减少量和离心力惯性势能的增加量是相等的，而动能又不变，所以在此非惯性系中小球机械能守恒.

深化拓展非惯性系机械能守恒定律，我们还可以利用它解决一些问题.例如：一小车在平直道路上向前以加速度a做匀加速直线运动，车厢内顶部悬挂一根长为l的轻绳，下端连接一个质量为m的小球，若将小球拉起至绳保持水平，从静止释放小球，如图3所示，求小球运动至最低位置时小球相对车厢的速度大小.

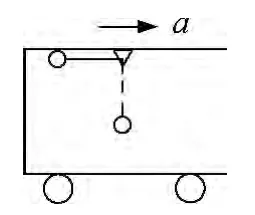
图3

分析：在这个问题中若以小车为参考系，由于小车具有水平向右的恒定加速度，所以此参考系属于相对惯性系做匀变速直线运动的非惯性系.小球要受到水平向左的惯性力f＝ma，由于惯性力为保守力，我们可以利用非惯性系下的机械能守恒定律来处理.由于该参考系没有转动情况，所以机械能中只有惯性力势能而没有离心惯性力势能，因此机械能守恒表达式简化为Ek＋Ep＋Ep惯＝Ek′＋Ep′＋Ep惯′.再变换为 ΔEk＝－ΔEp－ΔEp惯.

当小球从最高点落至最低点过程中，重力势能增量为－mgl，惯性力势能增量为mal，所以动能增量为

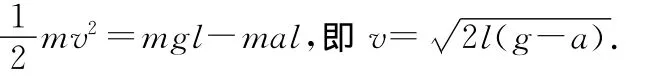
1 漆安慎，杜婵英.力学［M］.北京：高等教育出版社，2005.