离散广义系统的因果性
2014-01-06李莉莉崔利宏
李莉莉,逄 博,崔利宏
(辽宁师范大学 数学学院,辽宁 大连 116029)
离散广义系统的因果性
李莉莉,逄 博,崔利宏
(辽宁师范大学 数学学院,辽宁 大连 116029)
通常具有非因果性的离散广义系统在物理上是无法实现的,但实际系统中往往存在这种情况.本文首先讨论离散广义系统具有因果性的充要条件.然后针对不具有因果性的离散广义系统,证明存在状态反馈控制器和输出反馈控制器使闭环离散广义系统具有因果性的充要条件,并采用构造性方法分别针对rank(B)=r和不限制矩阵B秩的两种情况,给出状态反馈控制器和输出反馈控制器的设计方案,确保闭环离散广义系统具有因果性.
离散广义系统;因果性;Y-能控;Y-能观;受限等价形式;
0 引言
近年来,离散广义系统的研究已经取得了很大的进展,特别是针对线性时不变系统.但相对于连续广义系统,离散广义系统的研究还有很多方面未被涉及,且现有结果多数是建立在系统具有因果性的前提下.因果性是离散广义系统区别于正常系统的一个重要属性[1-4].离散的正常系统都具有因果性,但离散的广义系统并不总是因果的[5-7].通常不具有因果性的离散广义系统在物理上是无法实现的,这启发我们去寻找能够消除离散广义系统非因果性的方法,这在理论上和应用中都具有重要意义.文献[5]给出了当rank(B)=r时利用状态反馈控制器进行脉冲消除方法,但消除离散广义系统非因果性的方法还不多见,并且实际上B的秩并不总为r.本文分别通过设计状态反馈控制器和输出反馈控制器,在rank(B)=r和不限制矩阵B秩的两种情况下,确保闭环离散广义系统具有因果性.
1 预备知识
考虑线性时不变离散广义系统
Ex(k+1)=Ax(k)+Bu(k),
y(k)=Cx(k),
(1)
其中x(k)∈Rn,u(k)∈Rr和y(k)∈Rl分别为状态、输入和输出向量,E,A∈Rn×n,B∈Rn×r,C∈Rl×n皆为定常矩阵;E为奇异矩阵,且满足rank(E)=n0 (2) 其中 文献[6]指出离散广义系统(1)是因果的等价于连续广义系统(E,A)无脉冲,因此可根据连续系统(E,A)无脉冲的相关判据判别系统(1)的因果性.对非因果的离散广义系统,本节首先给出了存在状态反馈控制器使闭环离散广义系统具有因果性的充要条件.作为[5]中方法的延拓,当rank(B)=r时讨论消除系统非因果的状态反馈控制器方法.进一步在不限制矩阵B秩的情况下给出消除系统非因果性的条件和状态反馈控制设计方案. 给定非因果离散广义系统(1),若该系统Y-能控,找出状态反馈控制器u(K)=Kx(k)使得闭环离散广义系统 Ex(k+1)=(A+BK)x(k) (3) 具有因果性. 定理1存在状态反馈控制器使闭环离散广义系统(3)具有因果性的充要条件是离散广义系统(1)是Y-能控的. 首先考虑rank(B)=r的情况.由于离散广义系统具有因果性等价于连续广义系统无脉冲,因此寻找状态反馈控制器消除离散广义系统非因果性的方法与文献[5]类似. 例1考虑不具有因果性的离散广义系统(1),其中 上述方法虽然易于计算,但当rank(B)≠r时不再适用.下面考虑不限制B秩的情况. 定理2设可逆矩阵H1∈Rr×r,正交矩阵T1∈Rn×n,T2∈Rn×n,P∈R(n-n0)×(n-n0)和Q∈R(n-n0)×(n-n0)满足 T1ET2=diag{∑,0},∑=diag{σ1,σ2,…,σn0}, (4) PA22Q=diag{∑A,0},∑A=diag{τ1,τ2,…,τm}, (5) 并记 若系统(1)Y-能控,则使闭环离散广义系统(3)具有因果性的状态反馈控制器增益为 证明:系统(1)存在使得(4)成立的正交矩阵T1和T2[7],从而有 由系统(1)不具有因果性可知detA22=0.由(5)有 rank(A22B2)=rank(PA22PB2)=rank(A22)+rank(B22). 从而det(A22+B2K2)≠0,故可通过状态反馈控制器消除系统(1)的非因果性. 例2将例1中的矩阵B修改为 从而rank(B)=r不再满足,利用定理2可得 使得闭环离散广义系统具有因果性. 本节首先给出了存在输出反馈控制器使闭环离散广义系统具有因果性的充要条件,再针对rank(B)=r和不限制矩阵B秩的两种情况,分别给出能够消除系统的非因果性的输出反馈控制器设计方案. 定理3存在输出反馈使闭环离散广义系统具有因果性的充要条件是离散广义系统(1)是Y-能控能观的. 给定非因果离散广义系统(1),若该系统Y-能控能观且快子系统能观,找出输出反馈控制器u(k)=Fy(k)使得闭环离散广义系统 Ex(k+1)=(A+BFC)x(k) (6) 具有因果性. 定理4设非奇异矩阵Q1∈Rn×n,正交矩阵P1∈Rn×n和U1∈Rr×r满足 (7) (8) 证明:系统(1)存在使得(7)成立的Q1,P1和U1[5].设FC=K.系统(1)Y-能控,故由定理2可知存在FC=K使系统(6)具有因果性.由系统(1)Y-能观可知 例3在例2中的增加C=diag{1,1,1,0}的条件.利用定理3取 可使得闭环离散广义系统具有因果性. 下面考虑不限制B秩的情况. 定理5设可逆矩阵H1∈Rr×r,H2∈Rl×l,正交矩阵T1∈Rn×n,T2∈Rn×n,P∈R(n-n0)×(n-n0)和Q∈R(n-n0)×(n-n0)满足(4)和(5),并记 证明:与定理2类似,有 例4在例2中的增加C=diag{1,1,0,0}的条件.利用定理5取 使得闭环离散广义系统具有因果性. 本文为非因果离散广义系统设计了状态反馈控制器和输出反馈控制器,先利用连续广义系统消除脉冲的相关结论,给出rank(B)=r情况下,状态反馈控制器和输出反馈控制器的设计方法,然后又推广到矩阵B的秩不再受到限制的情况.相对于对已有结果使用范围更广,为消除离散广义系统非因果性带来极大方便. [1]程文彬,冯毅夫.新的量化反馈网络控制系统稳定性判据[J].吉林师范大学学报(自然科学版),2009,30(3):85~87. [2]杨晓光,张 强,刘公望.T-S离散模糊控制系统的稳定性研究[J].吉林师范大学学报(自然科学版),2003,4: 5~9. [3]李筱魁.智能变结构控制设计方法[J]. 吉林师范大学学报(自然科学版),2013,34(3):140~142. [4]戴立意.离散广义系统的求解和能控、能观性[J].数学物理学报,1989,9(2):129~138. [5]吴爱国.广义线性系统的脉冲消除与观测器设计[D].哈尔滨工业大学大学博士论文,2008. [6]杨冬梅,张庆灵,姚 波.广义系统[M].北京:科学出版社,2004,16-29,166-171. [7]段广仁.广义线性系统分析与设计[M].北京:科学出版社,2012,238~254. CausalityofDiscrete-timeSingularSystems LILi-li,PANGBo,CUILi-hong (School of Mathematics,Liaoning Normal University,Dalian 116029,China) In generally,discrete-time singular systems with non-causality are considered impossible in physics,which often exist in the practical systems.First,this paper discusses a necessary and sufficient condition of discrete-time singular systems with causality.Then for discrete-time singular systems with non-causality,the necessary and sufficient conditions for existences of state feedback controller and output feedback controller are proved to guarantee causality of the closed-loop systems.And state feedback controller and output feedback controller are designed respectively by constructive method for two cases of rank(B)=r and no requirement for the rank of matrix B which ensure the causality of the closed-loop discrete-time singular systems. discrete-time singular systems;causality;Y-causal controllability;Y-causal observability;restricted equivalent form 梁怀学) 2014-05-24 国家自然科学基金项目(61304056);辽宁省教育厅科学技术研究项目(L2013409) 李莉莉(1982-),女,辽宁省大连市人,现为辽宁师范大学数学学院副教授,博士.研究方向:控制理论. O231.1 A 1674-3873-(2014)03-0060-04
2 状态反馈控制器下的非因果性消除
2.1 问题描述
2.2 设计方法
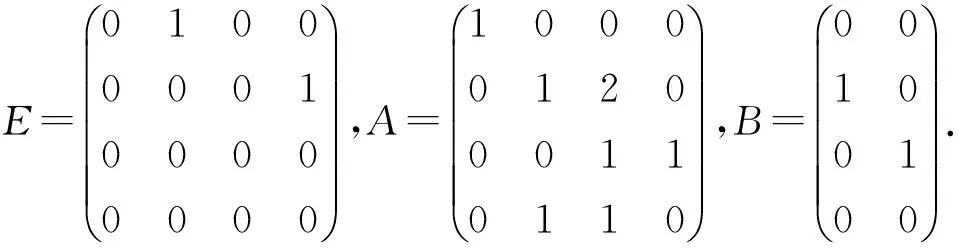


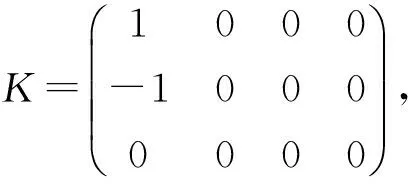
3 输出反馈控制器下的非因果性消除
3.1 问题描述
3.2 设计方法
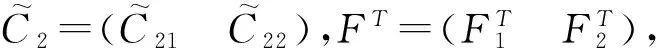
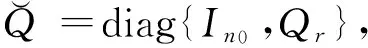
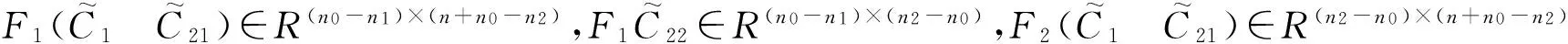


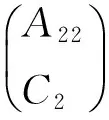


4 结论
