角形刚性阻振结构在船舶舱壁的应用研究

2014-01-04李守娟谢晓忠

船舶 2014年2期

徐伟李守娟陈林李卓谢晓忠

（哈尔滨工程大学船舶工程学院哈尔滨150001）

引言

船舶动力设备运行时产生的振动通过板架结构传递形成结构噪声，影响和危害船用精密设备和人员生活。从阻振隔振的角度，通过设计具有高传递损失的结构能够减小结构噪声，工程上一般在设备和基础之间配置弹性支撑或阻尼物质，能够减小振动。但这属于柔性隔振，由于船舶结构对强度的要求，柔性隔振在船舶阻振隔振的设计应用中受到限制，所以在实际应用中常常采用刚性减振技术。

在振动传递路径人为设计刚性结构，对振动的传递形成“障碍”，从而达到阻振、隔振的效果。这就是基于阻抗适配和波形转换理论刚性减振技术。刘见华运用波形转换理论研究了无限板上受点激励时单个或多个刚性阻振结构对振动传递的阻抑［1-2］；车驰东等运用波动分析法研究了附加在转角处的阻振质量对平面纵波、弯曲波振动能量的衰减作用［3］；姚熊亮、缪旭弘等进一步将刚性减振技术应用到船舶基座、舱壁等的设计和优化，取得了较好的效果［3-10］。但上述参考文献的刚性阻振结构都是基于矩形截面下的研究，并未设计多种刚性截面进行阻振、隔振性能对比分析形成最佳方案，因此，本文设计了多种不同截面的刚性阻振结构，并将其应用于船舶舱壁典型的“十”字结构处，数值分析了不同截面阻振质量带的隔振特性，并将不同截面特征的阻振质量带的隔振特性进行优化设计，所得结论对船舶减振降噪具有参考意义。

1 振动波垂直入射刚性阻振截面传递特性分析

图1为在板上采用刚性阻振设计的结构简图，不考虑振动波斜入射问题，这样可以取单位宽度的板结构进行研究，图中给出阻振质量突变截面变化处弯曲波各参数的变化情况，其中v表示质点的振动速度；表示质点的振动角速度；F、M分别表示力和力矩。

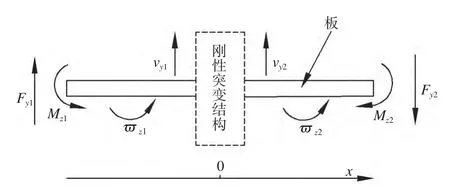
图1 板-刚性突变结构简图及参数

由图1可知：阻振质量为刚性，则在阻振质量截面处，左右两侧的横向速度和角速度应相等，即边界条件应为

而由于阻振质量的阻抗作用，两侧的力有如下关系：

式中：θ为突变阻振质量惯性矩（相当于单位宽度的值）；ω为圆频率。

由波动理论可知，当有一个从x＜0方向入射的正弦波v1e-ik1x（忽略与时间相关的简谐因子eiωt），它碰到突变截面时会产生反射波v1(re-ik1x+rjek1x)，式中：第一项表示反射回的向x＜0方向进行的波，第二项是由反射而产生的近场波。于是x＜0的区域总的速度为：

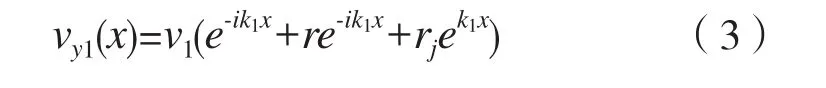
透过突变截面向x＞0方向传播的进行波为v1Te-ik2x，靠近截面处存在的近场波为v1Tje-k2x，于是在x＞0的区域内总的速度为：

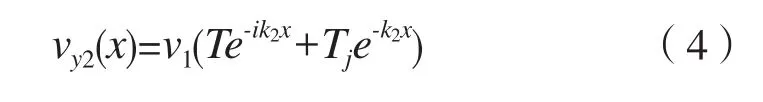
在上述各式中：r为反射系数；T为透射系数；k1、k2分别为x＜0和x＞0的钢板中的振动波的波数。

由结构力学知识可得：

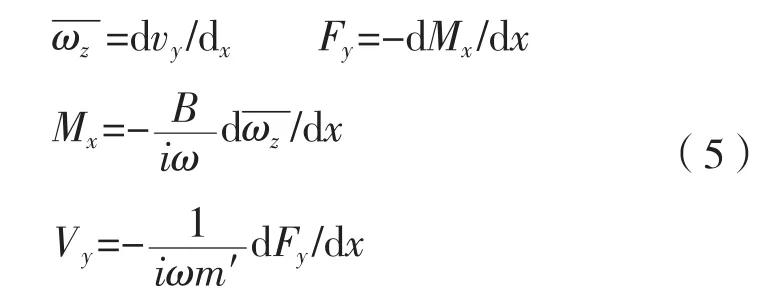
定义：

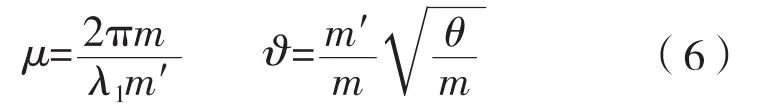
式中：B为弯曲刚度；

λ1为入射板中弯曲波的波长；

m′为单位面积板的质量。

将式（3）和式（4）代入式（1）、式（2）、式（5）和式（6）中得：

对于上面的四个参数，我们最关注透射系数T。当T=0时，出现全隔离频率，在全隔离频率处，刚性突变结构的减振效果最佳。该频率由透射系数T的表达式的分子为0求出。记全隔离频率所对应的μ为μs、为，则μs、应满足：

由此可见，阻振质量对振动波起隔离作用的主要参数是：刚性突变结构与板结构的质量比m/m′、刚性突变结构的质量惯性矩和板中振动波的波长λ1，而与刚性突变结构的绝对质量m无关。开展刚性阻振结构设计研究的意义就在于使全隔离频率落在关心频率范围内，从而最大限度地阻隔振动的传递。

2 多种刚性阻振结构应用在动力舱室的隔振性能分析

基于上文对刚性突变结构隔振性能的理论分析，从阻抗失配的角度出发，开展船舶动力舱室舱壁的刚性隔振设计，将设计的位置选定在动力舱室舱壁与其他舱室的交界处，并选取典型的十字结构进行设计研究，选择这一位置是因其处在振动由动力舱室向其他舱室传递的关键部位，在此处进行刚性阻振设计效果更好，其次十字结构往往是应力集中的位置，刚性阻振设计能够提高其强度，且在工程上便于实施。

本文针对十字结构设计了四种方案。如图2所示，图中1、2、3、4代表船舶舱壁结构，阴影部分代表刚性阻振结构的截面，将四种设计方案分别应用于图3所示的船舶动力舱室的简易模型，并使四种结构的截面积相等，图中黑色粗线表示设置阻振质量的位置。进行阻振设计后，在动力舱壁的四周形成了一圈闭合回路，称为阻振质量带，四种设计方案分别对应：方形阻振质量带、空心方形阻振质量带、角形阻振质量带、角形空心阻振质量带。为了方便工程应用，阻振质量带与同其衔接的舱壁采用同种材料。

图2 几种刚性阻振结构设计方案

图3 动力舱室简易模型

在如图3所示的基座上施加力F，采用有限元法数值计算了布置不同阻振质量带下结构的加速度响应，计算频率选为0～3 000 Hz，将计算出的加速度值转化为传递函数的形式，通过下式计算得到关心点的加速度传递函数值：

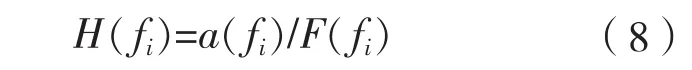
根据图3所示结构的对称性，在舱壁1、2、3分别选取n（n≥8）个关心考核点，得到加速度传递函数值，按下式计算其均方根，分别得到舱壁1、2、3的加速度传递函数均方值。

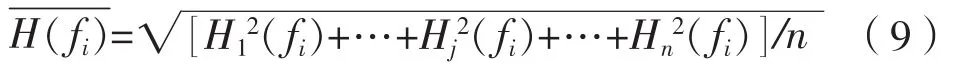
图4给出了在动力舱室布置方形和方形空心阻振质量带前后加速度传递函数值频响对比曲线。如该图所示：相对于未布置阻振质量时的加速度传递函数值，布置方形阻振质量带后，板1的振动加强，板2、板3的振动减小，一部分振动能量通过反射回到激励源所在的舱壁，方形/方形空心阻振质量对振动传递有阻隔作用；频率较低时，方形/方形空心阻振质量带对振动传递的阻隔作用较小，随着频率从1 000 Hz逐渐升高，隔振效果逐渐明显，大部分频率都有较好的阻振、隔振效果。

图5给出了在动力舱室布置角形和角形空心阻振质量带前后加速度传递函数值频响对比曲线。如该图所示：布置角形/角形空心阻振质量带后，板1在振动加强，板2、板3在全频段加速度响应减小，尤其在1 500 Hz以上范围内减小最为明显。由此可见，角形/角形空心阻振质量带能够很好地阻遏振动的传递，且其具有较好的传递损失特性，从而使板1的振动不致过于增大；对于角形/角形空心阻振质量带，当频率低于1 100 Hz时，两种结构振动加速度响应差异不大，但频率在1 300～2 300 Hz范围内时，角形阻振质量带的隔振效果较好，当频率高于2 300 Hz时，角形空心阻振质量带的隔振效果较好。

根据结构噪声评价标准，将船舶舱壁布置阻振质量带前后各位置的振级落差表示为：

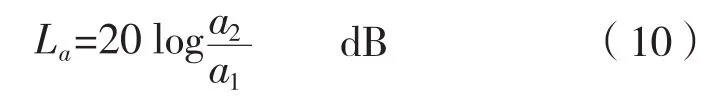
式中：a1表示原结构在计算频率内的加速度求和；a2表示原结构设置阻振质量带后在计算频率内的加速度求和；a1、a2的单位均为m/s2。

将上述频谱分量的加速度传递函数均方值相加，计算出各工况下各位置的振级落差，如下页表1所示。在保持板1振动未显著增大的情况下，角形结构和角形空心结构大幅减小板2、板3的振动加速度响应，相比较于方形结构和方形空心结构，阻振性能更好，因此在进行十字型舱壁交界处阻振质量应用设计时应选择角形（空心）阻振质量带。

图4 布置方形/方形空心阻振质量带加速度传递函数频响曲线

图5 布置角形/角形空心阻振质量带加速度传递函数频响曲线

表1 不同阻振质量带下的振级落差

3 刚性阻振结构截面特征优化设计

上文的研究表明，角形阻振质量带具有较好的阻振隔振性能，并进而在角形阻振质量带截面面积不变的情况下，改变角形的边长比，研究不同的角形截面隔振抑振性能优劣。如图6所示，截面2垂直于振动传播方向的边长较长，截面3与振动传播方向平行的边长较长（板1为振源所在平面），其中，图2中方案3为截面1，且各截面的面积相等。图6给出上述不同截面的角形阻振质量带加速度传递函数频响对比曲线，表2给出不同截面阻振质量带下各舱壁的振级落差。

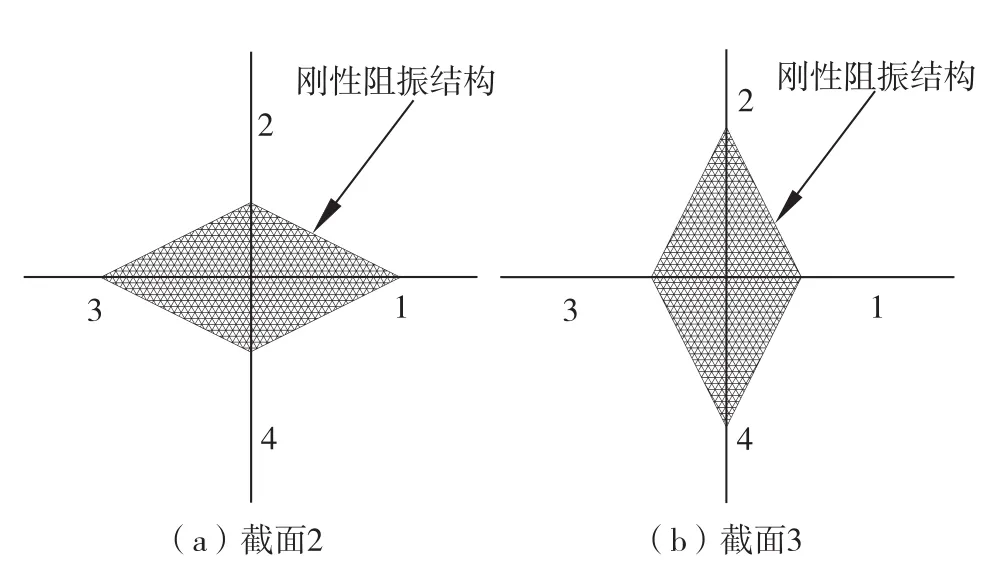
图6 不同角形阻振质量带截面示意图

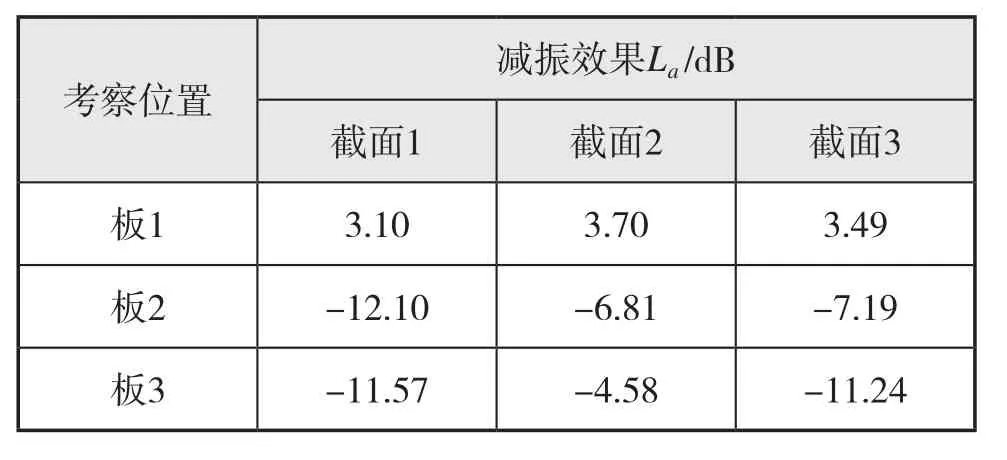
表2 不同截面阻振质量带下的振级落差

如图7所示：对于板1，频率较低时，各截面传递函数相差不大，当频率高于2 200 Hz，综合而言，截面3的加速度响应最大，截面1次之，截面2响应最小。对于板2、板3，截面2在1 800 Hz与2 800 Hz时存在加速度响应峰值，对应振动波全透射频率，总的说来，截面1对应的振动加速度传递函数最小，截面3次之，截面2最大。因此，结合各截面对应的振级落差，可以得出结论：三种角形截面中，截面1的阻振隔振性能最好。