常州地区三轴试验参数分析与研究
2014-01-03冯涛
冯 涛
(中铁第四勘察设计院集团有限公司,武汉 430063)
随着我国城市化建设的逐步加速,城市轨道交通建设迎来了新的建设高潮。区别于传统铁路勘察对岩土试验参数的要求,轨道交通对能模拟工况的三轴试验的需求越来越多。其中以CU试验最为常用,室内三轴试验是在太沙基提出的有效应力理论的基础上确定土体总抗剪强度参数c、φ值与有效抗剪强度参数c'、φ'[1]。本文通过对常州地铁1号线各土层的三轴试验结果,分析其相关参数的规律与异常并提出解决对策。
1 试验研究
1.1 试验设备与方法
试验仪器采用KTG全自动三轴仪,采用的试验标准为《铁路工程土工试验规程》(TB10102—2010),利用真空饱水机饱和,在常围压下进行应变控制的轴向压缩试验,取最大主应力差(σ1-σ3)max或者轴向应变为15%时对应的主应力差为抗压强度[2]。
1.2 试验理论
试验以库仑公式和莫尔圆结合建立的破坏准则莫尔-库仑破坏准则为基础[3],以不同围压下若干个试样破坏时的应力圆画出莫尔破坏包线,在一定围压区间里,可用直线表示,库仑公式为
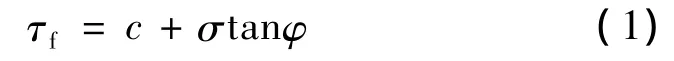
式中,τf为抗剪强度;c为黏聚力;σ为滑动面上的垂直应力;φ为内摩擦角。
根据极限平衡条件得到的总应力与有效应力平衡条件式为

式中,(σ1-σ3)f/2与(σ'1-σ'3)f/2分别为不同状态最大剪应力面上的剪应力,也是总应力圆与有效应力圆的半径;(σ1+σ3)f/2与(σ'1+σ'3)f/2分别为最大剪应力面上的法向总应力与法向有效应力,也是总应力圆与有效圆的圆心[4]。
2 异常参数分析
2.1 孔隙水压力系数A f
孔隙水压力系数的定义为:在三轴试验模型中Af为在偏应力Δσ1-Δσ3条件下的孔隙压力系数,当试样受到轴向应力增量作用下,产生的孔隙水压力为Δu2,其大小与主应力差Δσ1-Δσ3及土样的饱和度有关

式中,B为施加等向压力增量Δσ3条件下的孔隙压力系数,在饱和土体中,空隙被水填充,而水不可压缩,故Δσ3全部由孔隙水承担,故饱和土的B=Δu1/Δσ3=1。所以B的值也可作为判定土的饱和程度,饱和度越大,B 越接近1[5]。故 Δu=Δu2+ Δu1,而在 CU试验剪切过程中,Δσ3不考虑,原本的孔隙水压力消散,在剪切时的孔压为偏应力下的孔压增量
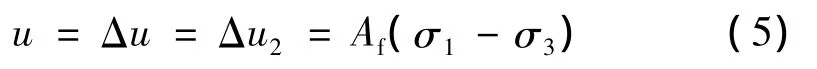
同时根据有效应力原理,土体由三相组成,土体在在剪切过程中产生孔隙水压力u,即σ=σ'-u,根据式(2)与式(3)可得,在应力差的强度包线图上,半径和圆心坐标分别为
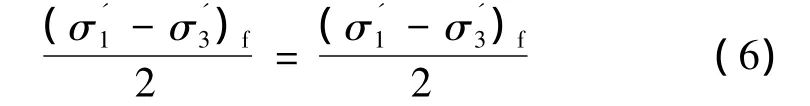
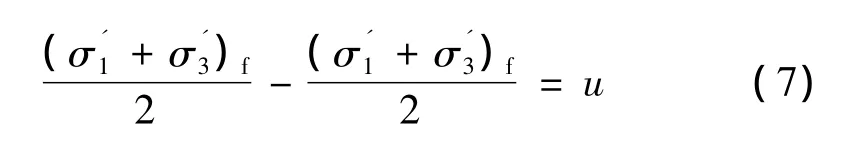
由此可在强度包线图上得出,有效应力圆等于总应力圆圆心平移了u的距离[6]。
然而在常州地铁三轴的实际试验中经常会遇到如图1所示情况。
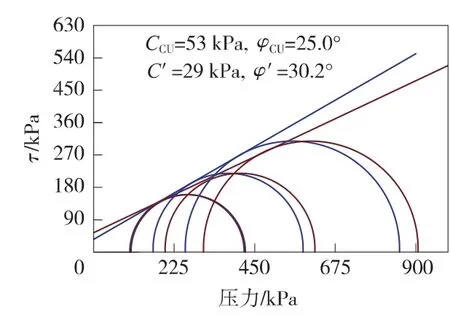
图1 应力差强度包线
如图1所示,分别进行100、200、300 kPa围压下的CU试验,测得其不同围压下破坏时的主应力差σ1-σ3分别为 316、418、605 kPa,Af值分别为 -0.02、0.07、0.08,由此根据前面的公式(4)、(5)得出破坏时的孔隙水压力为u100=-15 kPa、u200=33 kPa、u300=51 kPa。生成的应力差强度包线为200、300 kPa的有效应力圆相对总应力圆左移,而100 kPa围压的有效应力圆则右移。不同围压下应力圆移动的距离分别为-15、33、51。其中以往左移动为正,往右移动为负。通过对所做试验出现图1异常情况的部分土样进行统计分析如表1所示。
从表2中,我们可以看出出现Af为负值的基本为粉质黏土,且埋藏较浅,根据常州地区地质勘查报告得该地区理论上地下水位高,土体天然饱和。埋藏较浅的土层如表1编号1~5号基本上属于④1层,层低埋深6.9~13.8 m,时代为Q3al+l,土性均匀,为中等压缩性土[7]。通过对经典土力学的查阅,找到类似饱和黏土的经验Af值。

表1 土样物理性相关指标

表2 饱和黏土的A f值
对比可得,如要符合表2中Af为负数的情况,表1中的土必须均为超固结土或弱固结土。然而由于④1层埋藏较浅,对其进行先期固结压力试验,测算其先期固结压力值,结果如表3所示。

表3 先期固结压力结果
所以,根据其OCR的值,表1中的土均具有超固结结构特性,剪切时的孔隙压力系数Af将随着超固结比的增加而从正值减小到负值[8]。同时对比该土的主应力差、孔隙压力与轴向应变的关系,我们可以发现。
(1)在设置围压较低的情况下,土样为超固结状态,具有超固结特性的土,在剪切破坏时初始阶段为处于压缩状态,剪应力较小,这个阶段土颗粒被挤向更紧密的排列,与侧限压缩情况类似,随着主应力差继续增大,到达某一峰值,剪应力随着应变增大而较低,可以理解为颗粒与颗粒间的咬合作用逐渐丧失,颗粒产生错动,最后剪应力趋于稳定(图2),即所谓的残余强度[9],该现象也称作土的软化现象。图2中P3>P2>P1,可见软化现象也随着围压增而大越明显。

图2 主应力差-轴向应变曲线
(2)土体在初始剪切的时候,随着土样的压缩,空隙缩小,使得空隙水压力上升,即产生正空隙水压力使得有效周围压力减小来保持体积不变,反之随着土样剪胀,空隙增大,孔隙水下降或者为负值(图3),即产生负的孔隙水压力使得有效周围压力增加来保持体积不变[10]。同时围压的约束力越小,剪胀越容易,这就是为什么低围压下容易出现负孔隙水压力。
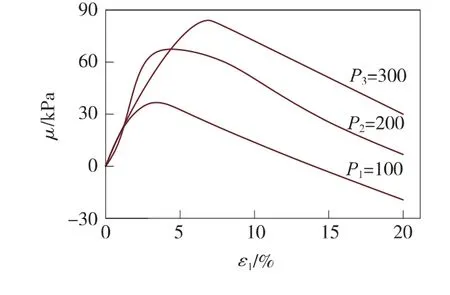
图3 孔压-轴向应变曲线
(3)三轴应力圆包线的计算是取剪切应变15%或者应力差峰值为破坏点,图3中的孔压峰值基本出现在应变5%作用,图2中的剪应力峰值出现在10%~15%,即2个参数不同步,所取得破坏孔压也不是峰值。
2.2 有效抗剪强度参数c'、φ'
在摩尔圆的强度包线图中,我们会得到两个不同的破裂面,继而得到效抗剪强度参数c'、φ'与总应力抗剪强度参数c、φ。在实际试验结果计算时,对这两组参数的选择常常存在争议,如图4、图5所示为CU试验中常见的两种曲线类型。
其中图4的曲线是经常出现的,而针对图5中两条破坏包络线几乎平行,造成c<c'的情况。尽管抗剪指标c和φ本质上是描述抗剪强度的数学参数而已,不代表真正的破坏位置[11],但在实际试验中,我们需要对取值进行调整,因此我们从剪切过程中,根据主应力差与孔压的变化,对不同破坏标准[12]来进行分析。
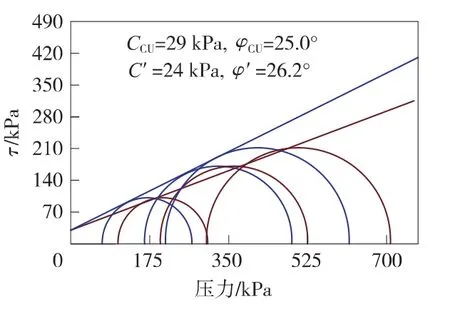
图4 应力差强度包线(一)
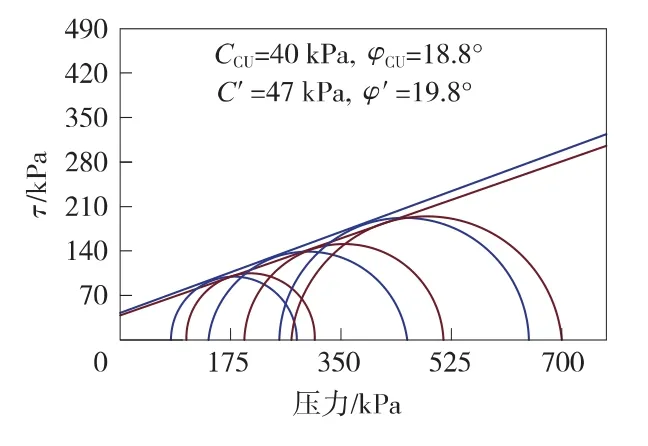
图5 应力差强度包线(二)
图4与图5土样的应力过程及不同破坏标准分别如表4中编号1、2所示,同时结合其孔压、应力差与轴向应变曲线(图6)可知1号土在剪切过程中主应力场一直在增大,孔压也在增大,在接近15%应变时达到峰值并开始减小,因主应力差没有峰值最后取15%的应变为破坏点,3个土样的应力、孔压曲线相似,路径与破坏标准一致。

表4 不同抗剪强度指标对应的破坏标准

图6 1号主应力差、孔压与轴向应变关系曲线
根据土样编号2的数据,结合其孔压、主应力差与轴向应变关系曲线(图7),可以发现,2号土样不同围压的土样,在剪切过程中主应力差、孔压都在增大,100、200 kPa围压的土样在孔压到达峰值后,开始减小,主应力差一直增大到15%应变为破坏点,而300 kPa围压的土样孔压没有峰值一直增大,直到应变到达13.5%,主应力差出现峰值作为破坏点,故300 kPa围压破坏点的判定标准与其他2个围压的土样不同。如要进行调整,可依据破坏标准进行重新画线,如图8所示,与前2个有效圆相切,得到的数据更可靠。编号3、4的破坏标准差别更大,其破坏时应变大都在5%左右,破坏点接近孔压峰值,其所得有效抗剪参数属于其特定剪切特征[13]。
由于三轴仪器的误差,以及土样的各向异性,不能保证在同样条件下土样的应变应力相同,因此如出现不同破坏标准的差异的土样,特别是那些c小于c'的试样(如表4中编号3、4),可做上1个超固结的土样,如果不考虑仪器带来的影响,同时土样是饱和的,那么有效应力圆圈将相对向右移了(即有效应力大于总应力),这样连出来的包线将合理一些。
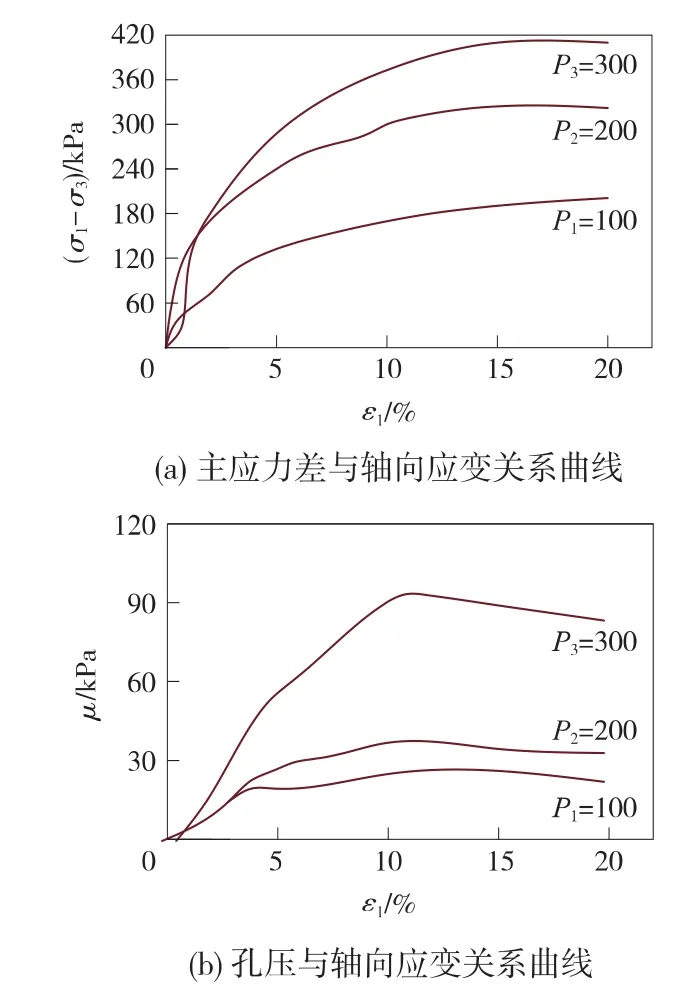
图7 编号2主应力差、孔压与轴向应变关系曲线

图8 调整后应力强度包线
3 结语
(1)三轴CU试验中,孔隙水压力系数B可作为初步判断土样饱和的指标,饱和度越大,B越接近1。具有超固结特性的土,在剪切过程中容易产生侧胀,导致孔隙水压力降低甚至为负,即Af变化从而影响有效应力摩尔圆的位置。
(2)抗剪指标c和φ本质上是描述抗剪强度的数学参数而已,它们是不具有物理意义,在三轴CU试验中,有效内摩擦角φ'>φ,这是经过实践和理论验证过的,而c值的大小不定,依据土样不同的破坏标准而不同。强度包线的选择依据多数土样相同的破坏标准而定。
(3)由于仪器的误差及常州地区土样的特殊性,本文的研究不一定具有普遍性,只针对常州本地土样特性。
[1] 陈愈炯.有效应力原理对饱和黏土的适用性[J].岩土工程学报,2011,33(6):159-162.
[2] 中华人民共和国铁道部.铁建设[2010]224号 铁路工程土工试验规程[S].北京:中国铁道出版社,2010.
[3] 李广信.关于有效应力原理的几个问题[J].岩土工程学报,2011(2):157-162.
[4] 殷宗泽,等.土工原理[M].北京:中国水利水电出版社,2007.
[5] 印文东.三轴剪切试验中孔隙水压力的特性探讨[J].城市道桥与防洪 ,2005(3).
[6] 李广信.高等土力学[M].北京:清华大学出版社,2004.
[7] 中铁第四勘察设计院集团有限公司.常州市轨道交通1号线一期工程四标——初勘报告[R].武汉:中铁第四勘察设计院集团有限公司,
[8] 徐舜华,徐光黎,等.土的剑桥模型发展综述[J].长江科学学报,2007,24(3):31-36.
[9] 姚海林,马时冬,卢应发.正常固结土与超固结土的一些特性及其应力历史的确定[J].岩土力学,1994(3):38-45.
[10]刘洋,宫志,等.超固结土三轴排水不排水试验数值分析[J].土木建筑与环境工程,2011(2):126-129.
[11]沈扬,葛东东,等.基于库仑定律的CU总应力切线和割线强度指标数理意义释义和适用性研究[J].岩土工程学报,2013(S1):52-59.
[12]陶元洪.客运专线铁路路基粉质黏土静三轴试验研究[D].成都:西南交通大学,2013.
[13]罗嗣海,杨建永.正常固结饱和土总应力强度指标的有效应力分析[J].东华理工大学学报:自然科学版,2008(1):73-76.
