最大熵法密度函数的求解及在桩板墙稳定分析中的应用

2014-01-03刘春刚

铁道标准设计 2014年1期

关键词：板墙概率密度函数线性方程组

刘春刚

(中铁第一勘察设计院集团有限公司，西安 710043)

1 最大熵法概率密度函数的确定和拟合

1.1 概率密度函数的确定

在概率论中，熵的定义［1］如式(1)所示

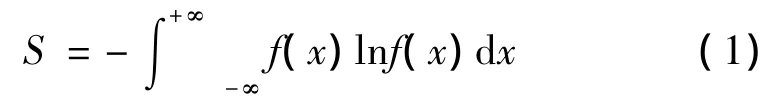
式中，S为熵;f(x)为概率密度函数。最大熵法的理论基础是最大信息熵原理:在给定所有满足约束条件的概率密度函数中，信息熵最大的概率密度函数为最佳的概率密度函数。设x为一个连续型随机变量，其概率密度函数f(x)满足以下条件

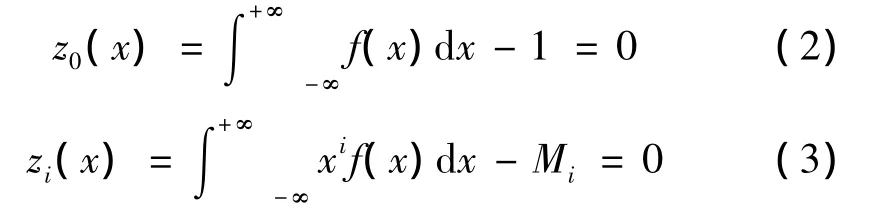
式中，Mi为x的i阶原点矩，可通过统计样本计算确定。这样最大熵法就转化为在式(2)、式(3)约束下求式(1)最大值问题。构造拉格朗日函数，如式(4)、式(5)所示

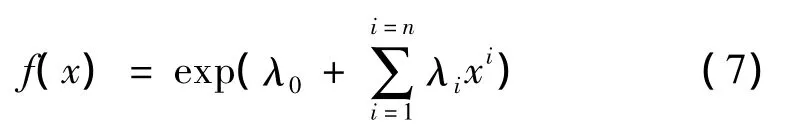
式中，λ0，λ1，λ2，…，λn为待定系数，由式(2)、式(3)构成的非线性方程组求解。

式(7)给出了n阶矩法概率密度函数表达式，韦征等［3］对n值的选取问题进行的研究，以一个单层网壳结构可靠度分析为验证算例，比较了最大熵理论三阶矩算法、四阶矩算法及五阶矩算法的计算结果。通过对比发现三阶矩算法得到的概率密度不能正确地反应结构位移响应变化规律，与四阶矩算法相比，五阶矩算法尾部误差较大，已经不能有效地提高概率密度函数、超越概率和可靠指标的精度，并且求解待定系数的方程组过于复杂，采用数值解法求解方程组时对初始值要求严格，不容易得到能使方程收敛的初始值。最终韦征等建议n值取4，即采用四阶矩算法。

1.2 拟合检验

根据最大熵原理求得函数只有通过拟合检验才能确定其性能的好坏，即能否最大程度反映随机变量本身概率特性。由于总体分布未知，在检验过程中自然就不会牵扯到总体分布的参数，对于这种总体参数未知的检验，被称为“非参数检验”，常用的非参数检验方法有K-S检验法、变量值随机性检验等，以K-S检验为例对最大熵法求得概率密度函数进行检验，其具体过程如下:

(1)原假设根据最大熵法得到的最大概率密度函数积分求得概率分布函数F0(X);

(2)利用样本数据计算个样本数据点的累计概率得到检验累计概率分布函数S0(X);

我国高铁走出国家的形势虽然良好，有着很大的潜力，但一些挑战是不可避免的，激烈的竞争、国际形势、未知的不利因素都是阻碍高铁发展的重要因素。

(3)计算F0(X)和S0(X)在相应的变量值点x上的差D(x)，得到差最大值Dmax;

(4)对于给定的检验水平α和样本容量n，查Kolmogorov分布的分位数表，得到临界值Dn;

(5)判断:若Dmax≤Dn时，则接受原假设，否则否定原假设。

2 概率密度函数的求解

最大熵法拟合概率密度函数的核心和难点在于以下非线性方程组的求解

式中，Mi统计样本 x的 i阶原点矩;λi为待定系数。

方程组的求解需要解决三方面的问题:①各方程积分域的选择;②方程组简化;③方程组求解方法。

2.1 积分域选取

方程组式(8)中各方程都含有一个不定积分项，直接求解非常困难，需要先把各方程的不定积分计算出来，去掉方程中的积分符号，简化方程组。由于被积函数比较复杂，需要人为的选择一个积分区域，用被积函数在该区域上的定积分代替原不定积分，然后采用数值方法进行积分运算。赵国藩［2］建议积分区域选为［μ-10σ，μ+10σ］并用梯形积分公式进行积分运算。通过算例对比发现积分区域的选取是否合适对拟合的好坏有重要影响。以均值为25，标准差为11.2极值Ⅰ型分布为例，当积分区域分别选择［0，400］和［0，80］时拟合的概率密度函数如图(1)、图(2)所示。

由图1、图2对比发现，积分区域取［0，400］时得不到正确的拟合函数，拟合的效果很差，最大误差为0.76。而积分区域取［0，80］时，最大误差量级为10-2，二者相差76倍。通过算例验证发现，积分区域应控制在［μ-10σ，μ+10σ］以内为宜，同时积分区间端点处对应的概率密度函数值不宜超过10-4。

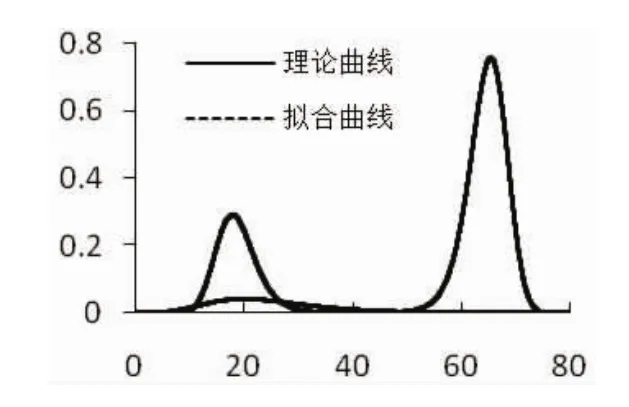
图1 积分域［0，400］

图2 积分域［0，80］

2.2 方程组简化

观察第一个方程，作以下变换

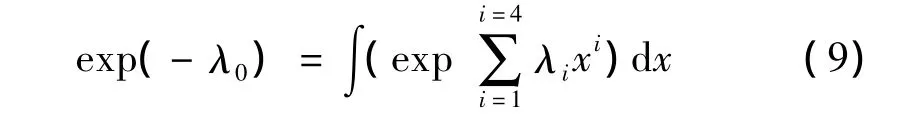
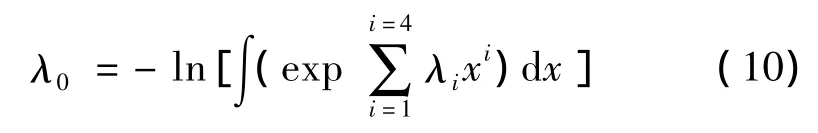
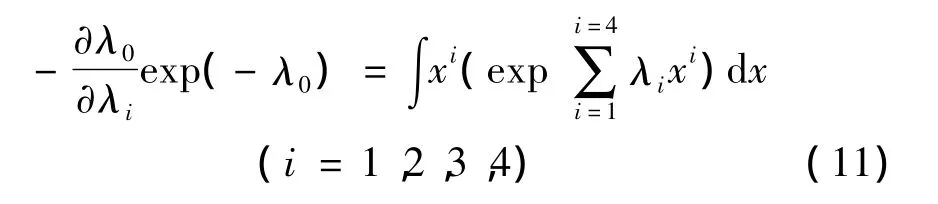
即

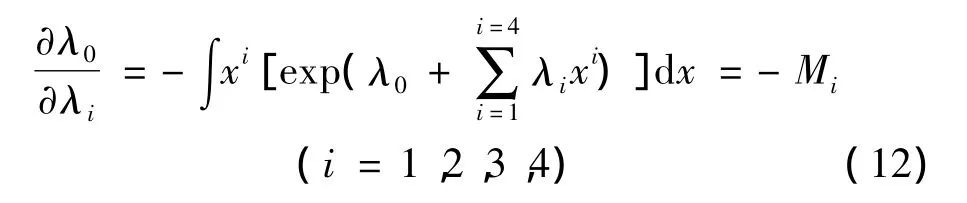
式(12)代入式(13)得

此时，最大熵法系数方程组就由式(8)化简为式(14)，即将原五元的方程组简化为四元的方程组，提高了方程组收敛速度和稳定性。由方程组(14)得到λ1、λ2、λ3、λ44 个系数后，按照式(10)求解 λ0，从而得到所有的待定系数。

2.3 方程组求解方法

非线性方程组(8)比较复杂，求解起来比较麻烦，已有许多文献对方程组的求解方法进行了探索研究。赵国藩等［2］利用循环中点求积Newton算法对非线性方程组牛顿算法进行改进，改进后的新算法具有收敛快、稳定、对初始值无限制，成功率高的优点。此外，还有一些文献［4-5］应用遗传算法、粒子群算法等优化算法求解，都取得了一定的成果。但是这些计算方法对数学知识要求较高，并且需要编写较为复杂的程序才能实现。

Matlab具有强大的数值计算能力，并且整合了许多优化算法、非线性方程组数字解法程序作为可以直接调用的内部函数，求解方程组比较方便。在求解实例时发现直接调用Matlab优化工具箱中的遗传算法程序去求解方程组(14)，不需要设置初始值，但是得到的解精度并不高，调用ga函数求解方程组一般上所能达到的精度为0.1～0.01，很难得到精度更高的解。在Matlab中还可以用Fsolve函数求解非线性方程组，该方法可以得到精度为10-7以及更好的解，但是使用Fsolve函数对初始解的要求非常严格，初始解选择不恰当将导致程序不收敛。比较上述两种算法的优缺点后，将两种方法有机的结合起来，先使用遗传算法得到一个精度为0.1—0.01的解，然后将这个解作为方程组的初始解调用Fsolve函数得到精度更好的解。这种方法前后两步都是直接调用Matlab内置函数，实现起来非常简单，并且求解成功率很高。本文分别用遗传算法和遗传算法与Fsolve相结合的方法对四种分布进行了拟合，四种分布的参数见表1。

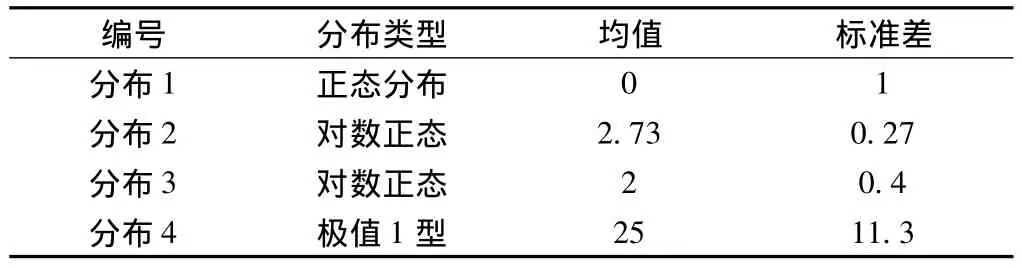
表1 分布参数

分别使用上述两种计算方法对上述四种分布进行计算，计算结果如图3～图10所示，其中图3～图6为遗传算法计算结果;图7～图10为遗传算法和Fslove函数相结合的计算结果。

对以上模拟结果的精度进行对比分析，结果如表2所示。

图3 分布1遗传算法拟合结果

图4 分布2遗传算法拟合结果

图5 分布3遗传算法拟合结果

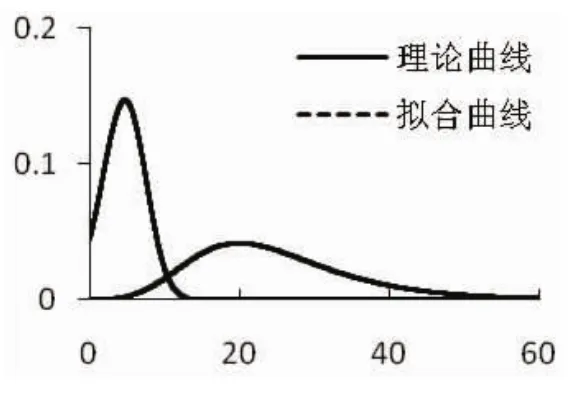
图6 分布4遗传算法拟合结果

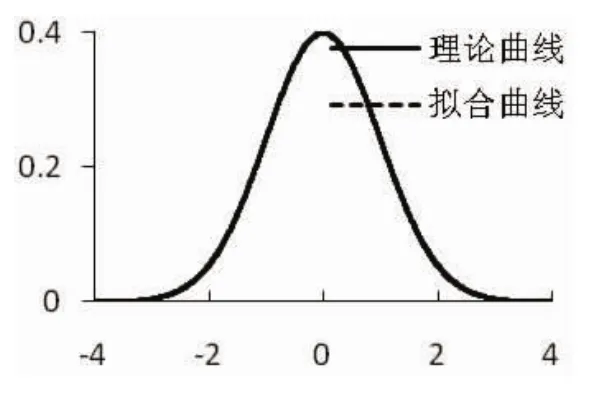
图7 分布1改进算法拟合

图8 分布2改进算法拟合

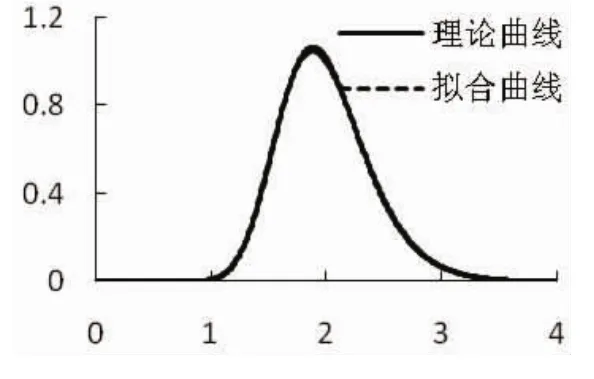
图9 分布3改进算法拟合

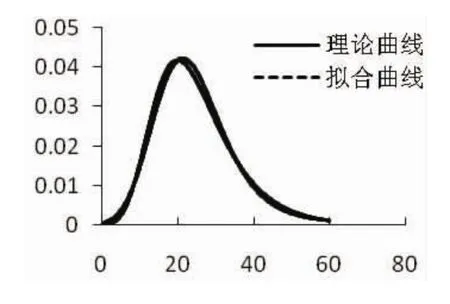
图10 分布4改进算法拟合

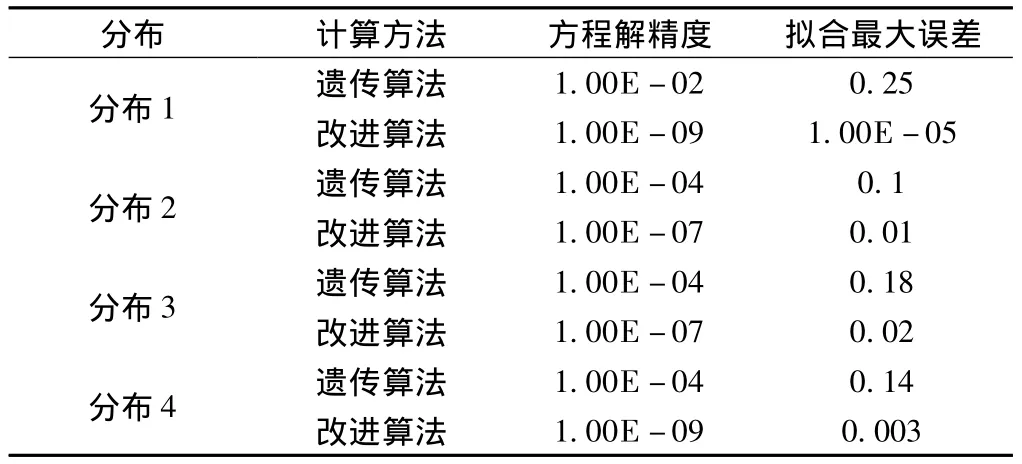
表2 各分部计算精度对比

由表2可以看出，单纯用遗传算法计算的结果精度不太高，概率密度函数拟合的误差在0.3～0.1之间，将这样的拟合概率密度函数代替真实密度函数进行可靠度计算会带来较大的误差。而采用遗传算法和Fsolve函数相结合的算法得到的拟合函数最大拟合误差均在0.03以下，精度较高。其中正态分布(分布1)拟合精度由原来的0.25提高至10-5，提高了2 400倍;分布3的最大拟合误差为0.02，代数与遗传算法相比精度提高了9倍。因此用遗传算法得到拟合函数的待定系数后，再以此结果为初始解用Fsolve进行一次求解，可以有效地提高计算精度。解决方程组(8)求解困难的问题，并且该方法直接调用Matlab内置函数，不需要编写实现遗传算法和非线性方程组数值解法的程序，实际操作起来简便易行。

3 桩板墙的极限状态方程与优化模型

3.1 极限状态方程

以路堑式桩板墙为研究对象，建立其可靠度分析方程，极限状态方程的一般形式为

式中，R为抗力;S为荷载。

桩板墙破坏主要是桩发生破坏，其破坏形式主要有受弯破坏、受剪破坏和锚固段内侧土体受压破坏三种形式，因此根据这三种形式求其极限方程。

按照式(15)极限状态方程的形式把受弯和受剪的极限方程分别表示为

式中，Ωpw、Ωpj分别为受弯和受剪计算模式的随机变量;Mmax、Qmax分别为桩板墙受到的最大弯矩和最大剪力;Mu、Qu分别为桩板墙极限弯矩和极限剪力。

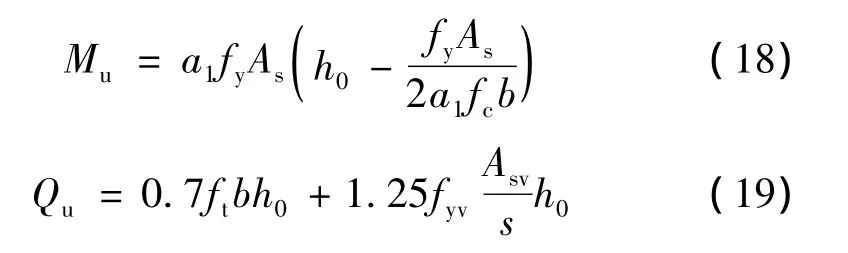
以“m”法为例

式中，A3、A4、B3、B4、C3、C4、D3、D4为关于桩埋深的函数;x0为滑面处的位移;M0、Q0分别为桩锚固段顶点的弯矩和剪力。对于式(20)和式(21)分别求一阶偏导为零，即可得到Mmax和Qmax表达式［6］。

3.2 随机变量的确定

综上所述，式(16)、式(17)为失效模式下的偏微分方程。对于抗力项随机变量，在式(16)中主要考虑纵向钢筋受拉强度fyu、纵向钢筋截面面积As、混凝土轴心抗压强度fcu、桩的截面宽度b和有效高度h0以及分项系数Ωpw;在式(17)中主要考虑箍筋受拉强度fyvu、混凝土抗拉强度ftu、桩的截面宽度b和有效高度h0以及分项系数Ωpj。对于荷载项由于计算复杂性，暂时直接按照分项系数法直接计算。

4 算例验证

以路堑式桩板墙为例，桩长23 m，桩间距6 m，桩采用2 m×3 m的T形桩，设计悬臂端长8 m，锚固段长15 m，悬臂端主要位于膨胀土和粉质黏土，锚固段主要位于圆粒土、强风化片岩和弱风化片岩中，局部位于粉质黏土中，其中设计土体容重取γ=18 kN/m3，综合φ=28°，内力计算按照“m”法，其中膨胀土取值3 000 kPa/m2，圆粒土和强风化片岩取值12 000 kPa/m2，弱风化片岩120 000 kPa/m，土压力分布按照三角形计算。桩底支撑采用自由端。

对于荷载的计算，利用铁一院研发的路基助手计算，其荷载分项系数按照K=1.35考虑，对于材料和桩的结构相关参数如表3所示。

表3 计算资料

对于弯矩利用最大熵原理求解得到，γ0=-0.919，γ1=0.020，γ2=-0.500，γ3=-3.03，γ4=0，失效概率为3.34e-8，可靠指标 β=5.399;同样对于剪力 γ0=-0.743，γ1=0.031，γ2=-0.459，γ3=-2.975，γ4=0.04，失效概率为7.95e-7，可靠指标β=4.864。