软件可靠性评估模块的研究与实现

丁春光

（工业和信息化部电子第五研究所，广东 广州510610）

0 引言

1983年IEEE计算机学会对 “软件可靠性”一词作了正式的定义。软件可靠性（Software Reliability）的定义：在给定的环境条件下和规定的时间内，软件不引起系统失效的概率，该概率是系统输入和系统使用的函数，也是软件中存在的错误的函数。软件可靠性工程（Software Reliability Engineering）中往往定义为：软件可靠性是软件产品在规定的条件下和规定的时间区间内完成规定功能的能力。软件可靠性是软件工程学与可靠性工程学结合产生的前沿学科，到目前为止软件可靠性学科的范围已经扩展到软件可靠性、软件维护性、软件安全性和软件保障性。

检验软件的可靠性可以通过软件可靠性建模和软件可靠性测试来完成，这两种方法是互补的而不是互相对立的。通过软件可靠性建模的办法，利用在软件测试阶段收集到的软件失效数据进行预计，以预计软件可靠性的实际水平，以便从可靠性的角度判断软件何时可停止测试。目前还没有被推荐为广泛应用的软件可靠性模型，虽然目前已建立了数百种软件可靠性模型，但均具有一定的局限性。因此，从软件可靠性模型的假设是否合理、实际应用是否简单方便、适用范围是否广泛等问题出发，如何进一步建立合理、实用的软件可靠性模型还有待于进一步研究。

软件可靠性模型选择时，重点考虑的是模型的预测精度。软件可靠性模型都是建立在一定的假设基础上。但是，有些假设并不合理甚至是不成立的，基于这些假设得出的数学模型也就无法对软件可靠性行为做出准确的预测。如何使建立的软件可靠性模型更符合实际的软件失效过程，如何选择一个更恰当的模型来评价一个软件的可靠性，对现有的软件可靠性模型如何评价它们的有效性和预测能力等一系列问题。于是，模型的预测准确性评价方法的研究就显得十分重要，目前得到公认的方法主要有：PL检验法、U-结构图分析法、Y-结构图分析法等。

软件可靠性评估模块（SRE）是由工业和信息化部电子第五研究所研制开发的五性工程软件CARMES 6．0中的一个模块。SRE通过采集软件失效数据，利用软件可靠性模型估计软件的可靠性。SRE主要包括模型参数的管理和软件可靠性的模型评估两大功能。SRE模块实现了7个软件可靠性评估模型。本文将对以上7种评估模型的实现原理及过程进行简单的介绍。

1 软件可靠性评估模型[1]

软件可靠性评估模块（SRE）可以处理以下7种模型：Schneidewind模型（S）、Jelinski-Moranda 模型(J-M)、Goel-Okumoto(NHPP)模型(G-O(NHPP))、Goel-Okumoto 改错不彻底模型 (G-O)、Schick-Wolverton 模型(S-W)、Moranda 模型(M)、Yamada-Ohba-Osaki(Y-O-O)模型。

1．1 Schneidewind 模型

基本假设：软件故障发生率满足指数下降。

评估参数：软件中初始故障发生率α；指数下降的比例因子β。

模型描述：设第i个缺陷的发现以及纠正时刻为ti，i=1,2，…,n,则在[ti-1,ti)间的软件故障率为常数

α和β的最大似然估计满足：

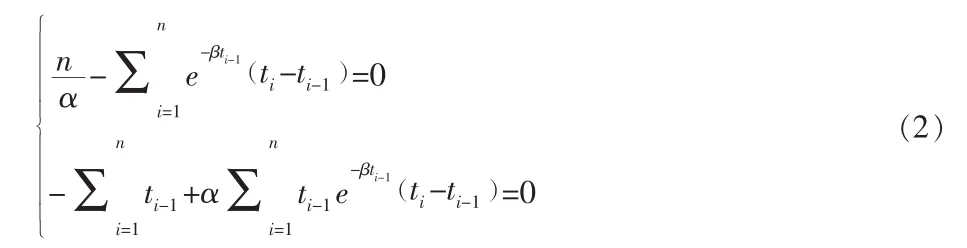
参数解特性分析结论：Schneidewind模型存在唯一解，P≤0时唯一解释合理解，P＞0时唯一解不是合理解。其中

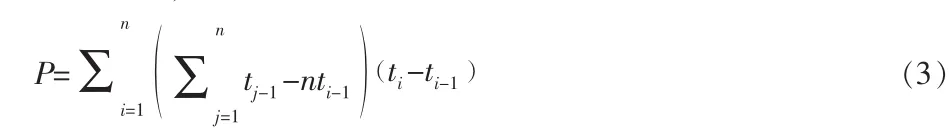
1．2 Jelinski-Moranda 模型

基本假设：软件故障发生率与软件中剩余错误的个数成正比。

评估参数：软件中初始错误总数N；单位故障发生率Φ。

模型描述：设第i个缺陷的发现以及纠正时刻为ti，i=1,2，…,n,则在[ti-1,ti)间的软件故障率为常数

N和Φ的最大似然估计满足：

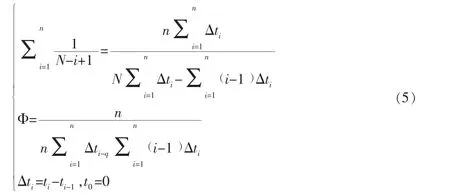
参数解特性分析结论：Jelinski-Moranda模型存在多组解，P≤时无合理解，时有唯一合理解，其中

1．3 Goel-Okumoto(NHPP)模型

基本假设：单位时间内发现错误的平均个数与软件中的剩余错误成正比。

评估参数：软件中初始错误总数a：错误发现率b。

模型描述：由基本假设，得出错误平均函数

设第i个缺陷的发现及纠正时刻为ti，i=1,2，…,n,则a和b的最大似然估计满足：

参数解特性分析结论：Goel-Okumoto(NHPP)模型存在唯一解，P≥1/2时无解，P＜1/2时唯一解（合理）。其中

1．4 Goel-Okumoto改错不彻底模型

基本假设：软件故障发生率与软件中剩余错误的个数成正比，但不向Jelinski-Moranda模型那样假设错误一旦发现即彻底改正，Goel-Okumoto假设错误的改正可以是不彻底的，即错误的改正度为q，q应大于零且小于等于1，值越大说明改错越彻底，q为1时为彻底改错，此时该模型等同于Jelinski-Moranda模型。

评估参数：软件中初始错误的实际总数N;单位故障发生率与错误改正度的比值Φ。

模型描述：设第i个缺陷的发现以及纠正时刻为ti，i=1,2，…,n,则在[ti-1,ti)间的软件故障率为常数

N和Φ的最大似然估计满足：

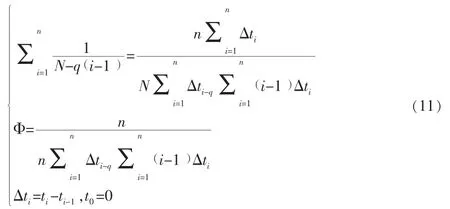
参数解特性分析结论：Goel-Okumoto改错不彻底模型存在多组

1．5 Schick-Wolverton 模型

基本假设：他们认为随着软件调试过程的深入,软件中的错误会越来越少,因此从总体上讲软件的故障发生率是呈下降趋势,但是在每次错误改正后投入继续调试以寻找下一个错误时,有时却随着调试时间的增加故障发生率是局部上升的,即时间越长越易出故障。该模型的故障发生率是一条呈锯齿性的变化曲线。

评估参数：软件中初始错误总数N;锯齿每次下降的幅度Φ。

模型描述：设第i个缺陷的发现以及纠正时刻为ti，i=1,2，…,n,则在[ti-1,ti)间的软件故障率为时间函数

N和Φ的最大似然估计满足：

参数解特性分析结论：Schick-Wolverton模型存在多组解，P≤

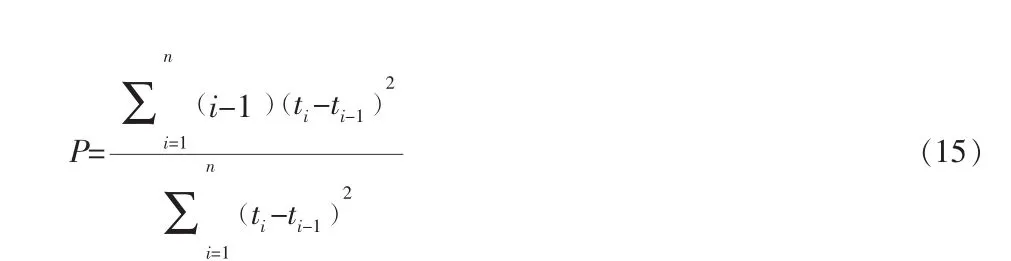
1．6 Moranda 模型

基本假设：软件故障发生率呈几何下降。

评估参数：软件中初始故障发生率D：故障发生率几何下降的比例常数k。

模型描述：设第i个缺陷的发现以及纠正时刻为ti，i=1,2，…,n,则在[ti-1,ti)间的软件故障率为常数

D和k的最大似然估计满足：

参数解特性分析结论：Moranda模型存在唯一解，P≥0时唯一解释合理解，P＜0时唯一解不是合理解。其中

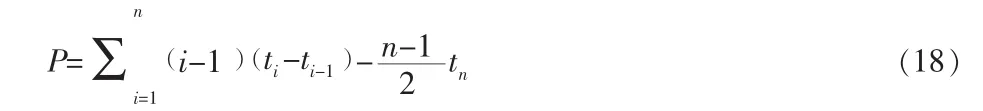
1．7 Yamada-Ohba-Osaki模型

基本假设：查出错误数的增长是S形,即开始增长缓慢,然后快速增长,最后趋于饱和。

评估参数：软件中初始错误总数a;稳定状态下的错误发现率b。

模型描述：假设S形的错误平均函数

设第i个缺陷的发现及纠正时刻为ti，i=1,2，…,n,则a和b的最大似然估计满足：

参数解特性分析结论：Yamada-Ohba-Osaki模型当P≥2/3时无解，P＜2/3时有唯一解（合理）。其中

2 软件可靠性评估模块（SRE）的实现

SRE主要包括模型参数的管理和软件可靠性的模型评估两大功能。

软件可靠性评估模块的模型参数管理分为软件错误统计数据组别管理和软件错误统计数据管理两个功能模块。

软件错误统计数据组别管理模块的数据格式如下：

组名：软件错误统计数据组别的名称：

错误统计数据描述：对软件错误统计数据的获取、检测方式等进行说明；

说明：对本组别的说明（可选）；

时间单位：软件错误统计数据的单位，可选择的时间单位有三个，小时、分钟和秒；

错误改进度：软件错误的改进程度；

软件错误统计数据的管理的数据格式如下：

序号：软件错误统计数据编号，于添加数据时系统自动生成；

间隔时间：软件发生故障的上一时间到本次软件发生故障的时间之差；

累计时间：本组别所有软件故障间隔时间之和；

软件可靠性评估模块实现了7个软件可靠性评估模型，通过计算可以得到可靠性指标及误差分析结果。得到的可靠性指标包括当前故障率、误差系数、MTTF、下一次故障可能时间。各个模型的评估指标计算公式如表1：

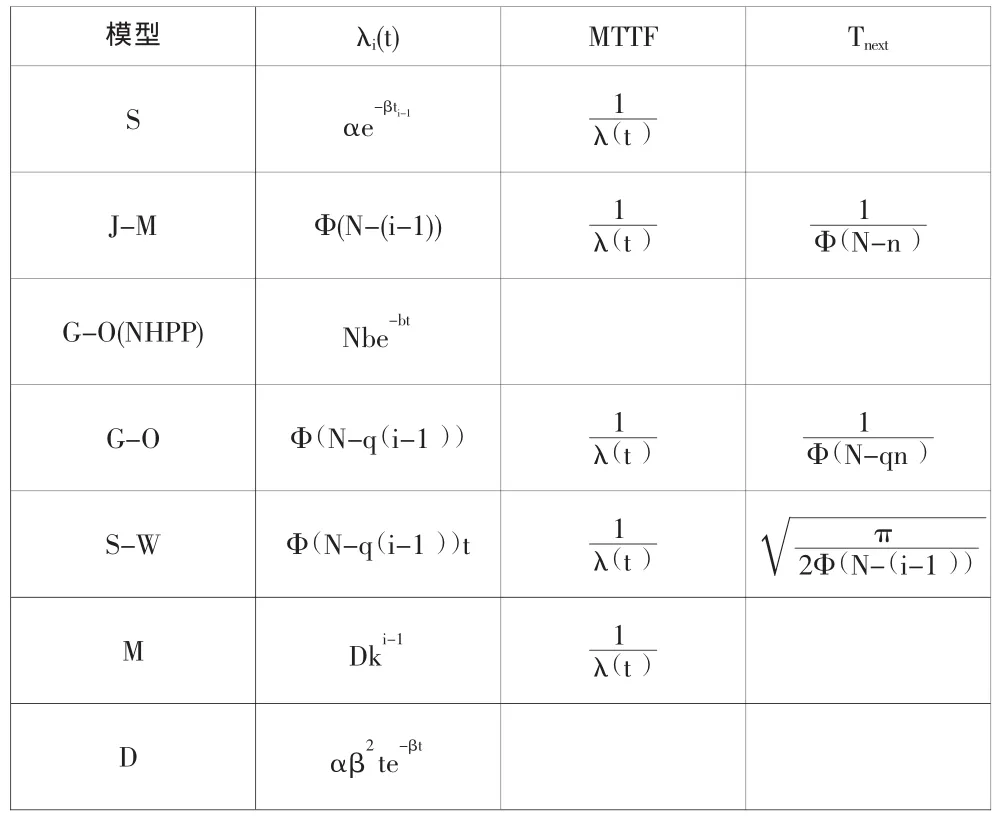
表1 模型评估指标计算公式

在进行模型评估计算时，需要指定错误统计数据的起始序号M，系统将抽取从起始序号开始到统计表表尾序号结束的该部分软件错误统计数据用于软件可靠性评估。因为随着软件开发过程的深入，程序中残存的错误会不断地被检出，并得到改正，软件故障发生的平均时间间隔将会逐渐变长，软件的可靠性会越来越高，此时软件开发的阶段将会改变。当软件进入新阶段时，新阶段的软件错误统计数据显然比前一阶段的数据更具参考价值，因此，用户可通过错误统计数据计算起始序号来选择不同阶段的统计数据用于软件可靠性评估。SRE模块界面如图2。

图1 CARMES 6.0运行主界面

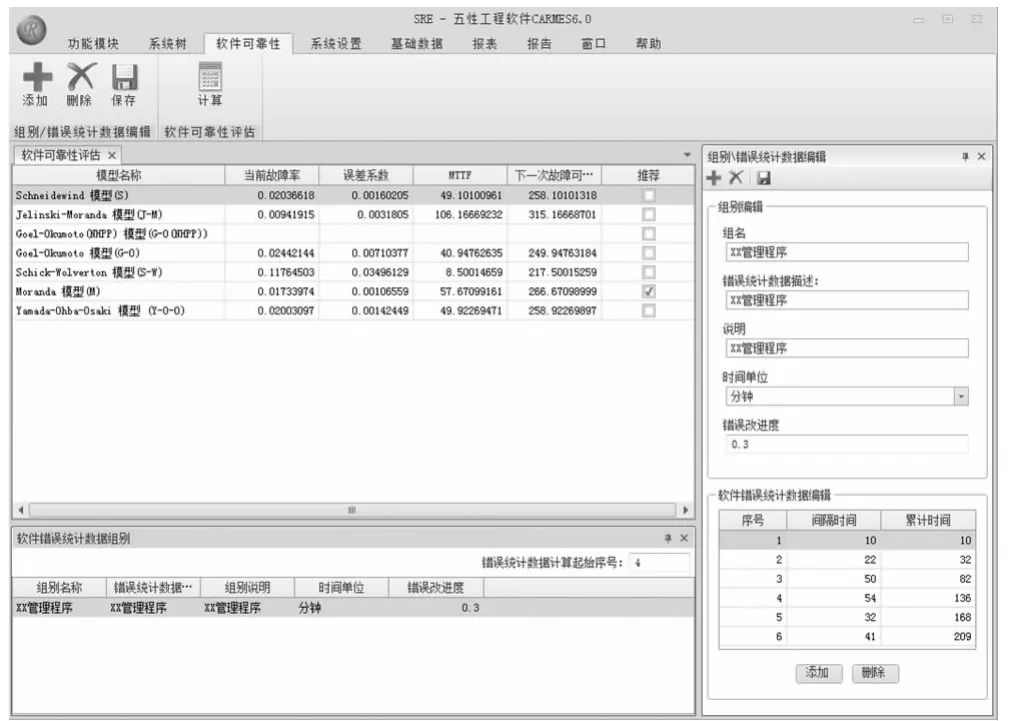
图2 SRE模块运行界面

3 结束语

软件可靠性评估模块（SRE）实现了7种软件可靠性评估模型，虽然还有一些模型有待实现，如Musa执行时间模型、Littlewood-Verrall模型、Seeding模型、Nelson模型，但已对软件可靠性评估模型的软件工程化进行了初步的探索，在以后的研究工作中将进一步逐步完善优化，形成一个强有力的软件可靠性评估工具。

[1]宋晓秋.软件可靠性与软件测试[Z].信息产业部军工电子装备可靠性工程技术中心.2002.10