一种用于海面贴近目标的距离维聚心改进方法

徐佳龙，黄晓刚

(海军驻南京地区航空军事代表室， 南京210002)

0 引言

在对海搜索雷达中，一般都使用普通脉冲体制，常用的海I模式就是采用低重频非相参处理工作［1］。在这类工作方式下，对贴近目标的分辨和跟踪是一个研究难点［2］，其中对目标信号的距离维聚心和方位维波束相关是处理中的关键环节［3］。

在常规的距离维聚心处理过程中，海面贴近目标会相互“遮蔽”，使参与方位维波束相关的点迹缺失或精度变差，合并后的目标信息不能满足对贴近目标进行准确的分辨和跟踪的要求。

本文首先介绍了常规的距离维聚心算法，列举了实际海面贴近目标检测中存在的问题，并在分析目标的距离方位特性的基础上，提出了一种改进型的距离维聚心算法，对贴近目标的分辨能力和测量精度有较为明显的改善。

1 海面目标的常规检测及存在的问题

1.1 海面目标的常规检测方法

常规检测流程如图1所示。在常用的海I模式中，一般以脉冲串为处理单位，非相参积累［4］后，可能会在一个或连续的几个距离单元有目标检出，如图2所示，第633～638号距离单元回波幅度高于恒虚警检测门限，视为有目标存在。

图1 常规检测流程图

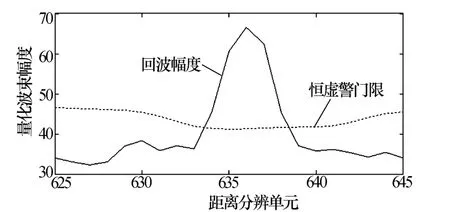
图2 恒虚警率处理结果图

针对目标在连续的多个门上都有恒虚警检测结果的现象，为了得出较为准确的距离信息，需要进行距离维聚心处理:首先，取检测报出的距离单元对应的滑窗非相参积累和，计算局部极大值和其左右相邻距离单元为

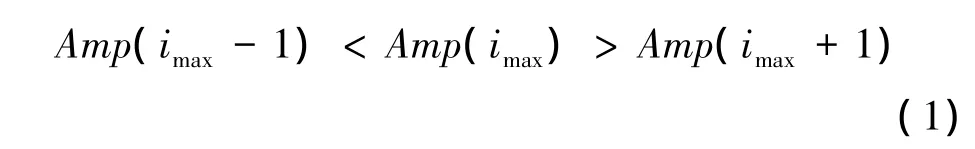
式中:i表示距离单元。取3个距离单元的幅度距离一次加权处理结果作为目标的距离值输出［5］

图2中距离维聚心的结果Rtarget=636.2。

其次，在脉冲串非相参积累后，经恒虚警检测，再距离维聚心可以得到目标的一组信息。随着波束指向的变化，对脉冲串做滑窗处理可以得到不同方位上目标信息，在方位维波束相关中，根据相关准则和波束结束准则，将多组距离维聚心输出的点迹信息做波束合并，可得到目标距离方位信息。

1.2 常规方法存在的问题

当两个目标在距离和方位上都比较贴近时，也会有连续多个距离分辨单元恒虚警检出，在距离维上和单一目标的特征相近，如图3所示。如果用常规的距离维聚心算法有时也只形成一个点迹信息，“遮蔽”了另一个目标。图3是一组贴近目标的实例。

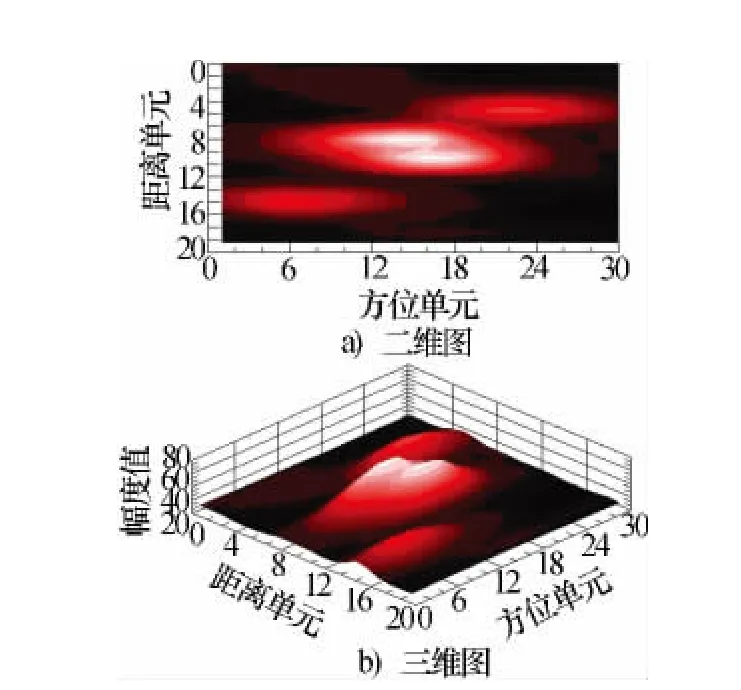
图3 贴近目标实例

图3a)中两个目标在距离上共占据约6个距离单元，中心相差约2个距离单元;两次滑窗处理形成的方位差计为一个方位单元，两个目标在方位向共计约18个方位单元，方位中心相差约3个方位单元。中心处相邻两个方位单元(图3a)中的第14、15方位单元)常规恒虚警检测结果如图4所示，图中573～593对应图2中纵轴的0～20。

按照式(1)、式(2)计算，图4a)极大值在586号距离单元，距离维聚心结果Rtarget=585.99，图4b)极大值在584号距离单元，Rtarget=584.11。从图3a)中可以看出，图4检测出的应该是两个目标，但方位维波束相关的门限通常大于两个距离单元，两个方位单元的检测结果将被相关上。作为一个目标信息，或是虽然没有被相关为同一目标，由于两个目标的方位维信息有缺失，使得方位维波束相关后目标的方位信息精度变差。

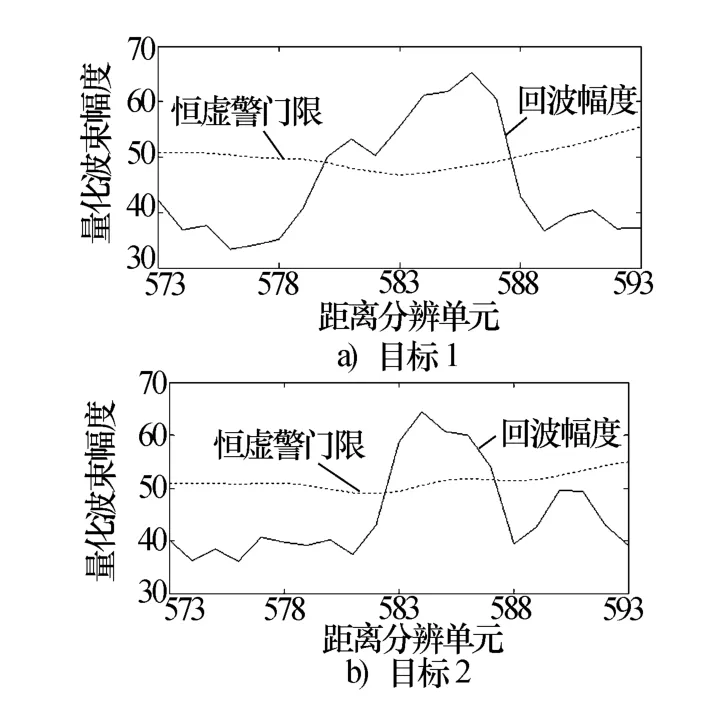
图4 常规恒虚警检测结果图

2 改进型的距离维聚心算法

2.1 海面目标的距离方位特性

目标的回波由于波束宽度和距离分辨率等因素，会在连续的距离单元和方位向上有高出背景的幅度，视频上呈粗眉毛状，如图5所示。海面船只是海面目标的主要组成部分，尺寸从几米至几百米不等，在距离维上表现出几个或几十个距离单元的回波特征。如果采样带宽较大，船体沿波束方向较长，结构比较复杂，连续距离单元幅度也会有相应复杂变化［6］，但对于检测常用的窄带信号，海面大小船只在距离上的幅度多呈包络状。

图5 海面目标距离维幅度特性和方位特征

天线的主瓣在3 dB范围内，增益指数可以用二次函数或角度函数逼近，它对点目标(大多数海面目标可以被认为是点目标)的回波在方位上起调制作用。同时，由于船体机构、雷达系统参数和和周围海浪回波的影响，点目标方位上回波幅度有一定的起伏，但能量集中在幅度较大的几个距离单元上，且幅度有相同的变化规律和较强的相关性，如图5所示。取图5b)中第5(虚线)、6(实线)、7(点画线)号距离单元，它们有类似的包络形状，其中中心处的6号距离单元有最大幅度。

常规的距离维聚心利用了距离维幅度包络，将跨越多个距离单元的目标信息加权处理，提高距离精度，但是这种基于滑窗内脉冲串的非相参积累的处理方法忽略了滑窗中带有的方位信息。所以，在检测距离相近，方位略微分开的目标时，如果距离维的幅度包络信息没有产生明显的分裂现象，会存在着较大的缺陷。

2.2 改进型的距离维聚心算法

针对常规距离维聚心算法的缺点，需要对恒虚警检测出的连续距离单元分析滑窗内的N个脉冲串对应距离单元幅度信息，计算检出距离单元内相邻单元方位幅度的相似性，如果相似值有局部极值，则在这两个距离单元间设定聚心分离点，在分离点两侧分别做常规的距离维聚心处理。由于滑窗内积累的脉冲数N有限，只能对N个方位单元的幅度信息做相似性计算。流程如图6所示。

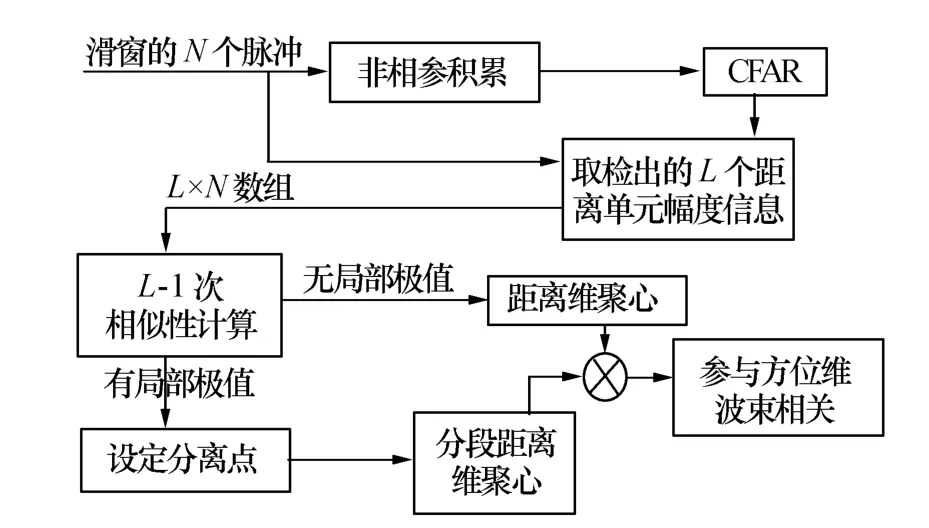
图6 改进型距离维聚心流程图

针对图4中实测数据按照流程算法，取出的L×N数组，记作 Al，j，l⊆(582，586)表示恒虚警检测出的连续距离单元，j⊆(1，N)表示滑窗中的脉冲，计算相似性 C(Ak，j，Ak+1，j，k⊆(582，585)，结果见表 1。

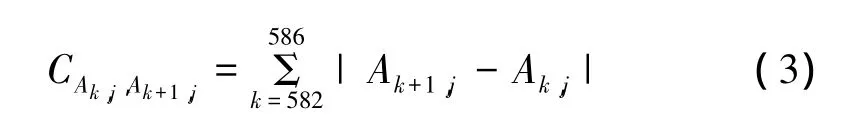
表1 相似度计算

如图7所示，第584、585号距离单元不具有单个目标在方位维的特征，在相似性计算中出现了局部极值点，可在第584号距离单元设定分离点。

分别在对分离点两端做距离维聚心，582、583、584的结果为583.01，584、585、586 的结果为584.90，这样就成功地将两个目标分开。

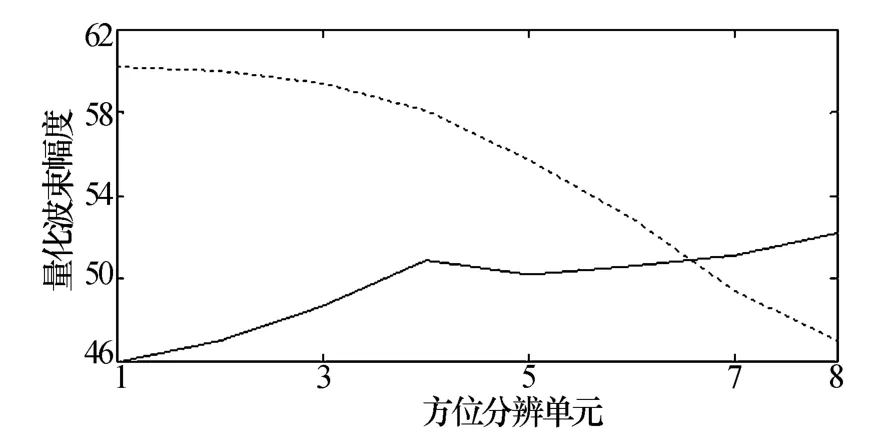
图7 分离点相邻距离单元方位维特征图

改进型距离维聚心算法仍然以脉冲串为处理单位，增加了检出单元信息提取和相似性计算，较常规型算法计算量略微增加，方便于工程中的实现。

3 分辨能力和测量精度的改善

使用改进型距离维聚心处理算法可以进一步改善海面贴近目标的分辨能力和测量精度。对图3实例使用常规距离维聚心和改进型距离维聚心算法，方位单元的聚心结果列举部分见表2。

表2 聚心算法与常规算法方位单元聚心结果的比较

在4～20号方位单元内两种算法都有目标检出，改进型距离维聚心在7～15号方位单元中还检出被“遮蔽”的目标。表中显示，在11、12号方位单元，常规距离维聚心检出的目标距离有约两个距离单元的阶跃，这是两个目标的脉冲串非相参积累和值大小发生了交替，如图4中所示，相邻第14、15方位单元的局部极大值发生的变化。

距离维聚心结果进行方位维波束相关，对满足相关准则的目标信息运用数中心、幅度加权或是幅度平方加权等相关算法。由于滑窗处理的影响，目标方位需要修正N/2。表3列举了相关准则不同时相关形成的目标距离方位信息结果。

表3 聚心算法与常规算法距离维聚心结果的比较

由图3和表3结果比较后可以看出，改进型距离维聚心的计算结果与实际情况基本一致。

通过大量实测数据验证，该改进算法基本有效。但是针对海杂波区内的小目标或是远距离目标时，由于回波幅度较弱，通常归一化信噪比小于10 dB，目标在方位维起伏较大，改进算法的使用将受到限制。

相似性门限的选择与波形时域频域参数有关，在2 MB带宽和距离分辨率为150 m的情况下，门限一般选择6。

4 结束语

海面的渔船或是舰船编队通常会密集排列，对于此类贴近目标，常规的距离维聚心在检测目标时存在缺陷。本文提出的改进型距离维聚心算法，不仅有利于对贴近目标进行有效分辨，还可提高测量精度，而且工程上也易于实现。

［1］ 贲 德，韦传安，林幼权.机载雷达技术［M］.北京:电子工业出版社，2006.Ben De，Wei Chuanan，Lin Youquan.Airborne radar technology［M］.Beijing:Publishing House of Electronics Industry，2006.

［2］ Lacomme P，Marchais J C，Hardange J P，et al.Air and space borne radar systems:an introduction［M］.New York:William Andrew Publishing，2007.

［3］ 吴顺君，梅晓春.雷达信号处理和数据处理技术［M］.北京:电子工业出版社，2004.Wu Shunjun，Mei Xiaochun.Radar signal and data processing technology［M］.Beijing:Publishing House of Electronics Industry，2004.

［4］ 李宗武.直升机机载雷达抗海杂波技术研究［J］.现代雷达，2000，22(1):10-14.Li Zongwu.Anti-sea clutter technology for airborne radar on a helicopter［J］.Modern Radar，2000，22(1):10-14.

［5］ 黄培康，殷红成，许小剑.雷达目标特性［M］.北京:电子工业出版社，2005.Huang Peikang，Yin Hongcheng，Xu Xiaojian.Radar target characteristics［M］.Beijing:Publishing House of Electronics Industry，2005.

［6］ 杨文琳，方志宏，阮信畅，等.雷达点迹凝聚处理技术及其数据分析［J］.信号处理，2001，17(2):130-138.Yang Wenlin，Fang Zhihong，Ruan Xinchang，et al.The radar plots centroid technology and data analysis［J］.Signal Processing，2001，17(2):130-138.