一种可配置高精度数控振荡器设计

陈亚宁，王 宁，张 磊，王少轩，赵忠惠，张紫乾，刘成玉，汪 健

(中国兵器工业集团北方通用电子集团有限公司， 江苏苏州215163)

0 引言

随着通信、卫星定位、数字电视、航空航天和电子技术等技术的发展，对频率合成器的要求也越来越高。各种新型的频率合成方案和频率合成器被相继提出，相关理论研究也不断涌现。从Colpitts振荡器到锁相环，研究人员一直致力于高分辨率、高稳定度、纯频谱振荡器研究。在现有的数字振荡器设计方法中，直接数字频率合成器(Direct Digital Frequency Synthesizer，DDS)以其独有的良好特性备受关注，已广泛应用在通信、雷达和导航等设备中。它既可以作为发射机的激励信号源，又是接收机的本地振荡器，在电子对抗设备中也可以作为干扰信号发生器。DDS易于集成，功耗低、体积小、可靠性高，最大输出频率可达百兆级［1-7］。

本文首先介绍了数控振荡器(Numerical Control Oscillator，NCO)的基本原理，给出了评估其性能参数的表达式。针对DDS相位累积器给出了具体实现过程，同时引入了改善相位截断以及幅值量化等杂散误差的分析。最后，介绍了NCO在数字下变频(Digital Down-Conversion，DDC)中的应用并对其性能结果展开了分析与讨论。

1 NCO原理

在数字信号处理中往往需要产生周期性的离散波形，这些波形可以是正弦波、三角波、锯齿波或方波，在整个DDC中NCO的设计相对较为复杂，其性能直接决定着整个DDC。产生NCO样本的方法包括实时计算法和查表法。以代表算法坐标旋转数值计算(Coordinate Rotation Digital Computer，CORDIC)为例，实时计算法在满足一定的精度条件下要求迭代次数足够大，增大了面积开销，仅适应于低频信号的产生［8-9］。NCO最常用的实现方法是查表法，即提前根据正余弦波的各个相位计算好相应的正余弦值，并以相位值作为查找表地址来存储各相位的正余弦样本［10-13］。查表法实现NCO结构如图1所示，每经过一个采样时钟，NCO的相位累加器就增加一个2πfc/fs的相位增量，其中，采样时钟频率为 fs，信号的输出频率为 fc。此时，以累加后的相位作为地址，选择输出查找表中相应的存储数据，得到该点的正余弦样本值。相位控制字用来设置本振信号的初相，频率控制字用来设置本振信号的频率。

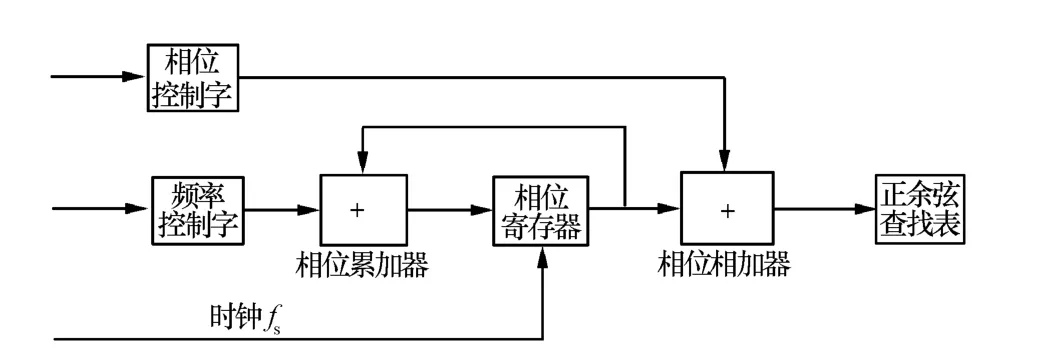
图1 查找表方式的NCO结构框图

设相位寄存器位数为N，采样时钟频率为fs，频率控制字为M，产生的信号的输出频率为fc，则有

基于Nyquist采样定理，最高合成频率受采样定理的限制只能达到采样频率的一半，而实际电路设计过程中为了保证输出精度，不会将频率控制字提高至最大值。

2 NCO设计

2.1 设计步骤

本文将采用查表算法来设计NCO，采用DDS技术产生对应频率的数字本振信号。如图2所示，为了减少芯片IO端口，采用串行码配置频率控制字dn，初始频率no，终止频率ns，经串并转换模块后同时送入累加器模块。NCO包括一个32位的相位累加器，根据输入的频率控制字产生相位累加值。取相位累加值的高12位作为地址，将存储在存储器中的数据输出即可得到对应频率的正余弦信号。比如本地振荡时钟为48 MHz，现需要产生12 MHz正交正余弦信号，设计中累加寄存器位宽N=32，根据式(1)，可计算出频率控制字M=32＇hC0000000。基于FPGA开发板平台，可调用IP core实现DDS功能，而在芯片内必须对NCO重新设计。

图2 DDS相位累加器

首先，利用Matlab软件生成基于相位的单周期正余弦幅值数据，利用Memory Compiler工具将所生成的数据固化在DROM存储器中，在此过程中会生成仿真所需的DROM verilog设计文件。

其次，根据设计原理要求，每隔一个时钟节拍将频率控制字与前一相位累加器输出结果值相加，取当前相位累加器输出寄存器高12位作为相位地址。

最后，利用计算出的相位地址去访问DROM中的相应正余弦幅值。

其中，只读存储器(Read-only Memory，ROM)容量为2K×W，K为相位截断位宽，W为 ROM的字长。ROM中字长的数量直接决定着相位量化误差，而字的位宽则关系到幅度量化误差的大小。在增大ROM精度的同时，其访问时间不容忽视，ROM大小每翻一倍，访问时间也随之翻倍，因此其最大读出频率不得不降低。为了降低因ROM面积过大而引起的功耗问题，本文在设计之初考虑了ROM存储正余弦数量，只存储正余弦的四分之一周期幅值(0～π/2)来增强电路可靠性，提高电路速度并减少成本。经过地址重映射和数据求补模块即可完成ROM压缩功能。在正余弦幅度值进行寻址时，首先确定地址信息对应的象限，再利用地址重映射模块对偏移地址值和正负符号进行修正，其具体修正方法见表1。

表1 地址映射偏移地址修正

2.2 误差分析

(1)相位截断误差分析

为了获取较高的频率分辨率，选取的相位累加器的位数为32位，如果把相位累加器输出的所有位数全部用来查询正余弦函数表，会极大的增加面积开销和成本，不利于芯片的稳定性。因此，对累加器相位结果进行相位截断，只取相位累加器输出的高12位用来查表，舍弃低20位。不可避免的是，查表的相位值将会产生误差，导致输出的正弦幅度值也产生误差，表现在输出的频谱上就会有杂散信号存在。

(2)幅度量化误差

幅度量化误差是因ROM存储能力有限引起的舍位误差，也可以认为是因数模转换器(Digital-Analog Converter，DAC)分辨率有限引起的误差。幅度量化误差在DDS输出谱上表现为背景噪声，其幅度远小于由相位截断和DAC非线性引起的杂散信号幅度，所以对ROM舍位的频谱分析又称为DDS的背景杂散分析。量化误差所引起的量化失真，用输出信号与量化噪声功率之比(Signal-to-Noise Ratio，SNR)来表征。当DAC满幅度输出时，有

式中:B是幅度量化的位宽。由此可知，若B=16，则幅度量化的信噪比可达到98.08 dB。尽管上述误差是不可避免的，但是通过选取合适的M(频率控制字)、fc(系统时钟频率)、N(累加器位数)和W(寻址位数)值，适当的D/A变换器和滤波器平滑台阶，所得到的波形可以很好的满足要求。

3 结果分析与讨论

利用Memory Compiler工具生成1 024行位宽为32的DROM:在SMIC 0.13 μm CMOS工艺下其面积仅为291.25 μm×157.310 μm。如图3 所示，在设计过程中，改变频率控制字，相位地址在原来的基础上连续变化，不会出现间断模式，保证了相位的线性连续性。图3给出了经过预置后的正余弦仿真结果，当配置信号wd_en有效时，dn、no、ns分别为频率控制字、初始频率、终止频率串行码，经过串并转换后sclr信号生效;当sclr高电平复位，频率控制字data设置为32＇hc0000000，输入频率 48 MHz，输出 12 MHz 正余弦波形，经核算波形满足上述要求。

图3 NCO配置变频仿真结果

将本文设计的NCO应用在DDC中，其应用框图和流片GDS II版图如图4所示，系统左上角部分为NCO，约占芯片面积的1/9。前级AD采样时钟fc=48 MHz，采样后的数据流经NCO产生的正余弦混频后实现，根据式(3)经过计算可以得到NCO设计频率分辨率

同时，根据式(4)可以得到信噪比SNR

为了更好的测试流片设计结果，本文将NCO配置成可变频模式。当dn、no、ns串行数据送入输入端口后，经并行转换在使能复位信号sclr信号生效之前控制NCO工作状态。将相位累加器前级结果进行二次累加即可实现变频模式，此时的输出正余弦波形如图5所示。可以看出，当频率较低时，由于每个周期采样点较多、相位地址足够，故波形较为圆滑;而随着频率的不断增大，特别是与采样频率处于同一数量级，单位周期内采样点大大减少，输出波形变得离散起来。在SMIC 0.13 μm工艺流片下，NCO面积仅为0.183 mm2，实现工作频率80 MHz。

图4 NCO在数字下变频中典型应用

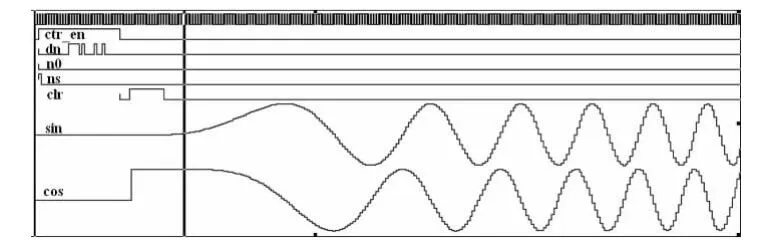
图5 可配置变换NCO I/Q支路结果

NCO的性能优劣直接决定着DDC。NCO的工作频率与带宽一直是DDC设计的优化目标，采用查找法利用相位地址直接访问存储器正余弦值，其频率计算速度直接取决于访问存储器的时间。在DDC芯片面积要求苛刻的条件下，选取相位累加器高位作为访问存储器地址，极大地降低了存储器容量，并不会影响频率分辨率。相位累加器32位地址完全满足高频率分辨率的设计要求，在较短的时间内实现可变频率正交波形。通过修正相位地址重映射，在ROM中也可存储三角波波形幅值，经过比较器输出占空比可调的方波波形，为后继时钟源提供了另外一种选择方案。

4 结束语

本文通过对DDC关键模块NCO的研究，设计了基于DDS的高精度、高信噪比动态可配置NCO，采用相位地址映射偏移和数据求补方法，极大的缩小了ROM面积。经过综合、静态时序分析，版图寄生参数提取，后仿及流片结果表明，该NCO设计频率分辨率可达0.011 76 Hz，实现信噪比72.24 dB，在变频模式下保持良好的线性相位输出连续特性。

［1］ Rohde U L，Whitaker J，Bucher T T N.Communications re-ceivers:principles and design［M］.2nd ed.New York:McGraw Hill，1997.

［2］ Rohde U L.Digital PLL frequency synthesizers:theory and design［M］.Englewood Cliffs，N J:Prentice-Hall，1983.

［3］ Turner C L.Recursive discrete-time sinusoidal oscillators［J］.IEEE Signal Processing Magazine，2003，20(3):103-111.

［4］ Tierney J，Rader C，Gold B.A digital frequency synthesizer［J］.IEEE Transactions on Audio and Electroacoustics，1971，19(1):48-57.

［5］ Guest D H.Simplified data-transmission channel measurements［J］.Hewlett-Packard Journal，1974，26(3):15-24.

［6］ 汤 励，曲秀杰.基于DDS的高可靠性雷达信号发生器设计与实现［J］.现代雷达，2012，34(11):73-75.Tang Li，Qu Xiujie.Design of the high reliability radar signal generator based on DDS［J］.Modern Radar，2012，34(11):73-75.

［7］ 李 静，徐芳明.一种新型多普勒天气雷达接收机的设计［J］.现代雷达，2013，35(3):62-64.Li Jing，Xu Fangming.Design of a new-type Doppler weather radar receiver［J］.Modern Radar，2013，35(3):62-64.

［8］ Chang Y K，Swartzlander E E.Digit-pipelined direct digital frequency synthesis based on differential CORDIC［J］.IEEE Transactions on Circuits and Systems:Regular Papers，2006，53(5):1035-1044.

［9］ Blinchikoff H J，Zverev A I.Filtering in the time and frequency domains［M］.New York:Noble Publishing，2001.

［10］ Yang Dayu，Dai Fa Foster，Ni Weining，et al.Delta-Sigma modulation for direct digital frequency synthesis［J］.IEEE Transactions on Very Large Scale Integration(VLSI)Systems，2009，17(6):793-802.

［11］ Mack A H，Trías M K，Mochrie S G J.Precision optical trapping via a programmable direct-digital-synthesis-based controller for acousto optic deflectors［J］.Review of Scientific Instruments，2009，80(1):101-103.

［12］ di Bernardo M，di Gaeta A，Hoyos Velasco，et al.Energybased key-on control of a double magnet electromechanical valve actuator［J］.IEEE Transactions on Control Systems Technology，2012，20(5):1133-1145.

［13］ Goryachev M，Galliou S，Abbe P，et al.Quartz resonator instabilities under cryogenic conditions［J］.IEEE Transactions on Ultrasonics，Ferroelectrics and Frequency Control，2011，59(1):21-29.