Fisher判别分析及其应用
2014-01-01田兵
田 兵
(包头师范学院《阴山学刊》编辑部,内蒙古包头014030)
0 引言
判别分析法是根据所研究个体的观测值来构建一个综合标准用来推断个体属于已知种类中的哪一类的方法,[1]这种统计方法在自然科学和社会科学的研究中会经常用到.因为所采用的标准有很多种,所以判别分析也有多种方法,其中Fisher判别分析是常用的判别分析法之一.[2]
1 数学思想
Fisher判别法的数学思想是将多维空间中的点投影到一维直线y上,使得由总体θ1和θ2产生的y尽可能分开,然后再利用距离判别法建立判别准则,进而达到判别个体所属群体的一种统计方法.[3]
1.1 两个总体的Fisher判别法
假设θ1和θ2为二维总体,如图1所示,“●”为θ1的点,“○”为θ2的点,按照原来的横坐标x1和纵坐标x2,很难将这两个总体的点分开,但是如果将这些点朝直线y上投影,形成一维空间点的集合,则能比较容易地分开.[4]

图1
显然,直线y是x1和x2的线性组合,即y=c1x1+c2x2.一般地,设在p维空间里,x的线性组合为y=αTx,其中:α为p维实向量,设θ1和θ2的均值分别为μ1和μ2,它们有共同的协方差阵∑,那么线性组合y=αTx的均值为

显然,使得μ1y和μ2y的距离越大的线性组合越好,所以考察以下比值

现在的问题转化为:如何选择α,使得(1)式达到最大值?
通过证明,我们有这样的结论:设x为p维随机向量,y=αTx,当α=c∑-1(μ1-μ2)(c为非零常数)时,(1)式可取到最大值.特别地,当c=1时,线性函数

称为Fisher线性判别函数.
当 y=(μ1- μ2)T∑-1x < μy时,则认为 x∈ θ2.
如果记W(x)=(μ1-μ2)T∑-1x-μy,则判别准则等价于:
当W(x)≥0时,则认为x∈θ1;当W(x)<0时,则认为x∈θ2.
在实际的计算中,总体的均值与协方差阵未知,就需要用样本均值与协方差阵来代替.即用样本均值1和2分别代替μ1和μ2,用样本的协方差矩阵来代替.这里的S1和S2分别是两个样本的协方差阵.[5]
1.2 多总体Fisher判别
如果变量很多或者有多个总体,通常要选择若干个投影,即选若干个判别函数来进行判别.
设有 k 个总体 θ1,θ2,…,θk,有共同的协方差阵∑,θi的均值为 μi.令
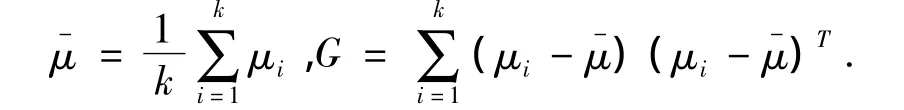
考虑p维随机向量x的线性组合y=αTx,α为p维实向量,则y的均值和方差为
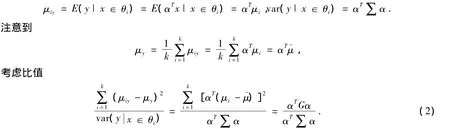
现在的问题在于:如何选择α,使得(2)式达到最大值.为了方便起见,设
我们通过下面的结论来解决这个问题:
设 λ1≥ λ2≥ …≥ λs> 0为∑-1G的s个非零特征根,s≤min(k-1,p),e1,e2,…,es为相应的特征向量且满足eT∑e=1,那么a1=e1时,使得(2)式达到最大值的解,称为第一个判别函数,而a2=e2时,在约束条件之下使得(2)式达到最大值的解,称为第二个判别函数.如此下去,as=es是在约束条件之下使得(2)式达到最大值的解,称为第s个判别函数.
当总体的均值和协方差阵未知时,通常采用样本均值和样本协方差阵来代替.和两个总体的Fisher判别法类似,也可以建立多个总体的Fisher判别规则.[5]
2 实例
在研究沙基液化问题中,选了7个因子.从已液化和未液化的地层中分别抽取了12个和23个样本,具体数据见表1.其中Ⅰ表示已液化,Ⅱ表示未液化,试用Fisher判别法对上述样本进行判别分析.

表1 沙基液化与未液化样本数据

28 Ⅱ 7.5 52 1 6 6 0.16 40 29 Ⅱ 7.5 52 1 7.5 8 0.16 40 30 Ⅱ 8.3 97 0 6 5 0.15 180 31 Ⅱ 8.3 97 2.5 6 5 0.15 180 32 Ⅱ 8.3 89 0 6 10 0.16 180 33 Ⅱ 8.3 56 1.5 6 13 0.25 180 34 Ⅱ 7.8 172 1 3.5 6 0.21 45 35 Ⅱ7.8 283 1 4.5 6 0.18 45
我们发现这是一个两个总体判别分析的问题,可以通过Fisher判别分析法来进行判别.首先计算两个样本的均值和协方差阵,可以得到

进一步可以得到样本的协方差阵为:

所以,样本的Fisher判别函数为:
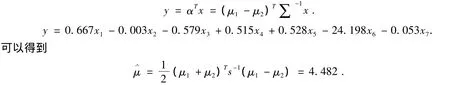
因此有判别准则

将给定的样本 x0=(a,b,c,d,e,f,g)代入到上述判别准则.如果 W(x)≥ 0,则认定 x0∈ θ1;否则x0∈ θ2.例如第 11 号样本 x11=(7.8,172,1,3.5,14,0.21,45),可以得到

所以第11号样本属于已液化的沙基样本.
将所有样本进行回代,我们可以得到如下结果:
第 9 号样本 x9=(7.5,52,3.5,7.5,6,0.16,40),
可以得到 W(x)=-0.6539488<0.
所以第9号样本应该属于未液化的沙基样本.
[1]黄利文.改进的Fisher判别方法[J].福州大学学报(自然科学版),2006,34(4):473-474.
[2]李建军,丁正生,张海燕.常用判别分类方法分析[J].西安科技大学学报,2007,27(1):138-139.
[3]潘劲松.Fisher判别分析及应用[J].数学的实践与认识,2013,43(5):155-156.
[4]费宇.应用数理统计:基本概念与方法[M].北京:科学出版社,2007.
[5]薛毅,陈立萍.统计建模与R软件[M].北京:清华大学出版社,2007.
