数字等高线边界问题处理算法优化研究
2014-01-01勾朝阳
勾朝阳
(忻州师范学院地理系,山西忻州034000)
0 引言
数字化等高线的过程中,会出现等高线首尾节点与区域边界不连接,或等高线首尾节点超出区域边界外(图1),使后期处理工作量增加,一般在原有矢量等高线上直接手工校正,但工作量非常大.因此,利用原有矢量化等高线直接自动处理的方法是值得研究的课题[1].
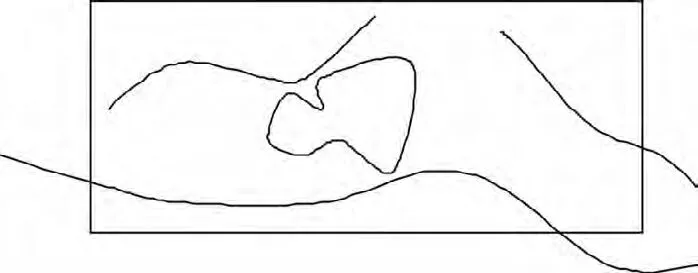
图1 未处理等高线边界
1 数据结构
算法的执行效率与数据结构之间存在密切的关系.一个良好的数据结构有利于对数据进行高效的管理,从而提高算法的执行效率[2].数据结构如下:

2 算法思想
2.1 算法原理
第一步,判断等高线是闭合曲线还是开放曲线.如果为闭合曲线则继续判断下一条,如果为开放曲线则进入第二步.
第二步,搜索等高线首节点和尾节点,判断首节点或尾节点是否在边界上.如果在边界上则继续判断下一条等高线,如果不在边界上则进入第三步.
第三步,判断等高线首节点或尾节点是在区域边界内还是在区域边界外.[3]如果在区域边界内,则转入第四步,否则转入第五步.
第四步,(1)线头的延长.等高线第一点和第二点所在直线与相应边界区域求交点并记录,将此交点作为等高线的首节点.
(2)线尾的延长.把等高线倒数第一点和倒数第二点所在直线与相应边界区域求交点并记录,将此交点作为等高线的尾节点.
第五步,(1)线头的裁剪.继续判断等高线第二点和第三点等等直至找到出现在区域边界内的一点为止并记为(xi,yi),求线段(xi-1,yi-1)(xi,yi)与相应区域边界的交点并记录,用此交点作为等高线的首节点,重新生成等高线.
(2)线尾的裁剪.继续判断等高线倒数第二点和倒数第三点等等直至找到出现在区域边界内的一点为止并记为(xi,yi),求线段(xi-1,yi-1)(xi,yi)与相应区域边界的交点并记录,用此交点作为等高线的尾节点,重新生成等高线.
2.2 算法流程图

图2 算法流程图
3 算法实现
3.1 判断等高线是否为闭合曲线

3.2 判断首节点和尾节点是否在区域边界上


3.3 判断首节点和尾节点是否在区域边界内
3.3.1 判断首节点是否在区域边界内


图3 首尾节点均在边界内

图4 首节点在超出边界,尾节点在边界内

图5 首节点延长至边界上
3.3.2 判断尾节点是否在区域边界内
尾节点处理方法与首节点相同.
3.4 判断每个节点是否在区域边界外

图6 首节点均超出边界

图7 第i个节点在边界内
3.4.1 从第二个节点开始向后判断


3.4.2 从倒数第二个节点开始向前判断

图8 尾节点超出边界

图9 第i个节点在边界内

4 实例应用
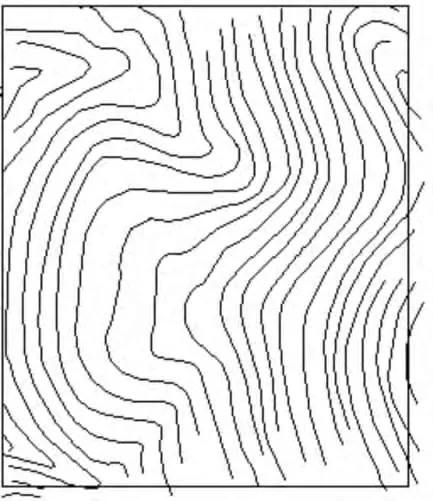
图10 处理前等高线

图11 处理后等高线
本文很好地解决了引言中所提出的问题,程序不仅适用于所有矩形边界的同类问题,而且通过边界的变换,可以推广至不规则复杂边界的同类问题.
5 结语
本文算法结构简单明了,内外共两层for循环,外层为等高线条数,内层为区域边界数,因而时间复杂度为O(1),运行效率较高.但随着等高线数据量的增大,需要的内存空间会有所增加.
[1]李峰婷,陈性义,赵礼剑,等.矢量等高线自动内插加密分析[J].工程地球物理学报,2004,(1):183-185.
[2]沈雷,李翔,邵培南.C/C++软件测试工具的元数据结构设计与实现[J].计算机工程,2008,34(13):43-48.
[3]张宏,温永宁,刘爱利.地理信息系统算法基础[M].北京:科学出版社,2006.30-32.
[4]刘勇奎.图形裁剪算法研究[J].计算机工程与应用,2005,(21):18-23.
[5]李雪,石广田.任意多边形窗口的有效线裁剪算法[J].兰州交通大学学报(自然科学版),2007,26(3):41-47.
