时域反射测量计在微波电路仿真中的应用
2014-01-01李晓明姜海玲郭文刚
李晓明,姜海玲,郭文刚
(中国电子科技集团公司第五十四研究所,河北石家庄050081)
0 引言
TDR是一种经典的微波测量仪器,在微波测量中可得到阻抗不连续点的物理位置和阻值信息。这些信息在点频测量中是无法获得的[1,2],在实际微波电路设计、调试中起着重要作用。TDR的典型应用包括断点、故障点测试[3],谐振腔体研制及调整中的精细测量[4],传输线特性阻抗的测量和控制[5,6]等。TDR的测试结果通常反映为沿传输线方向各点的特性阻抗[7]。按实现原理分,TDR测量仪器可分为时域TDR和频域TDR两类:时域TDR使用时域函数发生器作为信号源,如传统TDR厂商Polar、Tektronix等公司的产品;频域TDR使用扫频信号发生器作为信号源,通过频域合成得到TDR所需脉冲函数,从而实现TDR功能[4],如Agilent公司的部分矢网(E5071C)。时域TDR仪器价格低,但功能较为单一,适合生产单位使用;频域TDR仪器通常较贵,但兼具频域、时域测试能力,使用灵活,更适合科研单位。与国外产品对比,国内TDR特性阻抗测量系统偏倚性、稳定性还有待提高[8]。
随着计算机运算能力的不断提高,仿真技术已在微波电路设计中起到越来越重要的作用[9,10]。TDR的概念源于微波测量,但随着计算电磁学的发展,也被逐渐被引入微波电路仿真中。一些商用软件,如 ANSYS 公司的 HFSS、Agilent公司的 ADS[11]和CST公司的CST MICROWAVE STUDIO等都集成了时域TDR求解器。此外,学术界也对TDR在电磁计算中的应用保持着相当的热情[12,13]。采用TDR求解可获得不连续性的位置和阻抗,在微波电路设计中可对电路结构的优化进行有效指导,典型的应用包括射频接头的设计、信号完整性分析等。时域TDR求解器所得结果除包括TDR阻抗曲线外,还蕴含更丰富的信息,然而对许多设计而言,TDR可提供需要的信息,且结果简单直观,使用更为方便、快捷,值得进一步研究和推广。本文采用TDR仿真技术,对同轴短截线和金丝键合两种不连续结构进行了匹配和补偿,得到了明显的回波改善。
1 时域TDR工作原理
TDR的工作方式类似于雷达,或者说类似于蝙蝠和海豚的回声定位,其工作原理是,由函数发生器发送一个脉冲信号f(t),由取样示波器探测反射(回波)信号的特性和延迟来推断出不连续性的特性和位置,如图1所示。其中,TEE是一个T型结,DUT是待测设备。
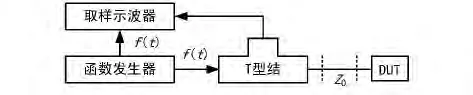
图1 时域TDR系统组成原理
假设DUT为纯TEM系统,且只存在一个阻抗不连续点,其电路如图2(a)所示。在这种情况下,不会有多次反射,回波损耗与频率无关,故不会造成信号失真。进一步假设函数发生器产生的是冲击函数信号,则可绘出TDR测量的工作原理如图2(b)所示。
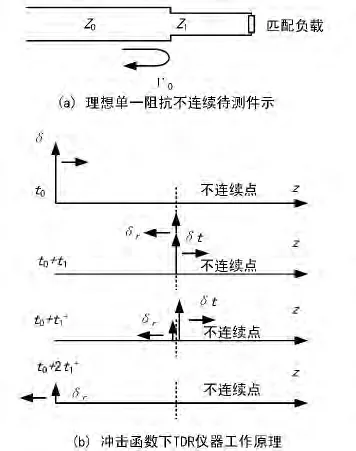
图2 TDR工作原理
图2中,δ为入射信号函数,δr=Γ0δ为反射信号函数,横坐标z表示位置。δ信号在t0时刻发出,经过时间t1后到达不连续点并处于临界反射状态,δ函数分裂为前向信号δt和反向信号δr,但此刻仍在同一位置叠加;t0+t1+时刻,δt和 δr完全分裂并向相反方向传播;再经过时间t1,即t0+2t1时刻,反射信号回到激励点。根据信号的往返时间、传输线上的电磁波速和反射信号的电平,即可确定不连续点的位置和不连续处的反射系数,并可进一步计算求得不连续点后传输线的特性阻抗Z1。
根据传输线理论,图2中的反射系数Γ0可由式(1)计算。式中,Z0为不连续点之前的特性阻抗,也就是测试系统的特性阻抗,而Z1则是不连续点之后的特性阻抗。

反过来,如果已知不连续处的反射系数,则可根据式(2)求得该点之后传输线的阻抗值:
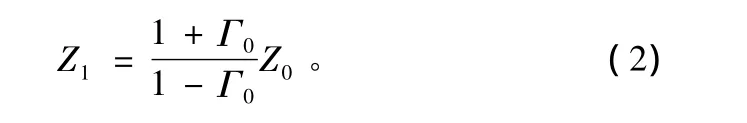
尽管冲击函数测量精度高,但在实际测试或仿真系统中无法实现。实用激励函数包括阶跃函数和高斯函数。阶跃函数即上升矩形脉冲,实现较为简单,使用这种激励可通过式(3)得到阻抗Z随时间变化的函数Z(t):
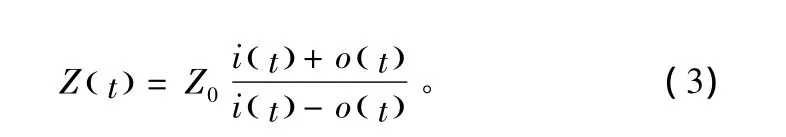
式中,i(t)为输入信号函数,在时间轴正向为常数;o(t)为反射信号函数;Z0为测试系统的特性阻抗;Z(t)为阻抗随时间变化的函数。在实际应用中,这一函数可根据测试系统及DUT中的光速方便的变换为阻抗Z随位置变化的函数。
图3是根据式(3)计算阻抗曲线的示例。其中图3(a)为电路阻抗随位置分布图,图3(b)为计算得到的阻抗随位置变化的曲线。
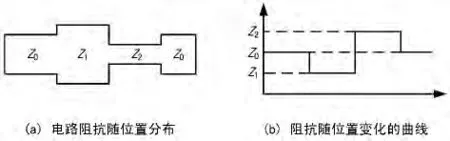
图3 TDR方法阻抗计算示例
在TDR仿真计算中,更常用的激励信号是高斯脉冲,其一般形式为:

与阶跃函数相比,高斯脉冲函数在时域具有有限的能量,更适于数值计算。采用高斯脉冲作为激励信号时的阻抗函数Z(t)如下所示:
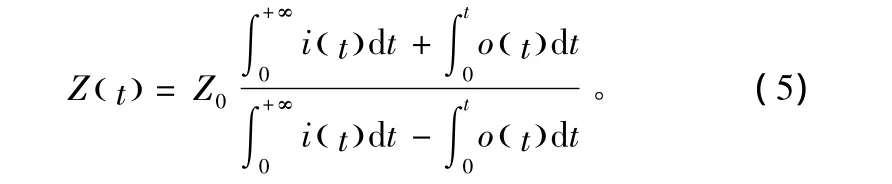
式中,i(t)、o(t)、Z0、Z(t)的含义与式(3)中相同。
2 TDR在微波电路仿真中的应用
使用电磁数值仿真技术解决问题时,TDR所求得的阻抗变化曲线对消除电路中不必要的反射具有直观的指导作用,可方便地对射频接头的形状和装配方式进行优化。美国Southwest Microwave公司即使用CST Microwave Studio的TDR求解器,针对旗下的End Launch接头进行了装配方案的优化,并在高达50 GHz的频率范围内显著改善了输入驻波。现以2个具体的例子说明TDR在微波电路仿真中的应用价值。
2.1 同轴低阻线的阻抗匹配
假设50 Ω同轴线上存在1 mm长的低阻段,其阻抗为45 Ω,如图4(a)所示,这显然是一个非匹配结构。图4(b)和图4(c)分别给出了HFSS仿真得到的TDR阻抗曲线和频域S11参数曲线。在时域仿真中,使用脉宽为17.52 ps的高斯脉冲信号,而不连续性的总长度为1 mm,其对应的电磁波传输时间为 3.34 ps,双程传输时间为 6.68 ps。在图 4(b)中,曲线TDRz(P1)和TDRz(P2)依次为从图4(a)同轴低阻线端口1、端口2激励得到的TDR阻抗曲线,由于结构的非对称性,两条曲线并不重合。
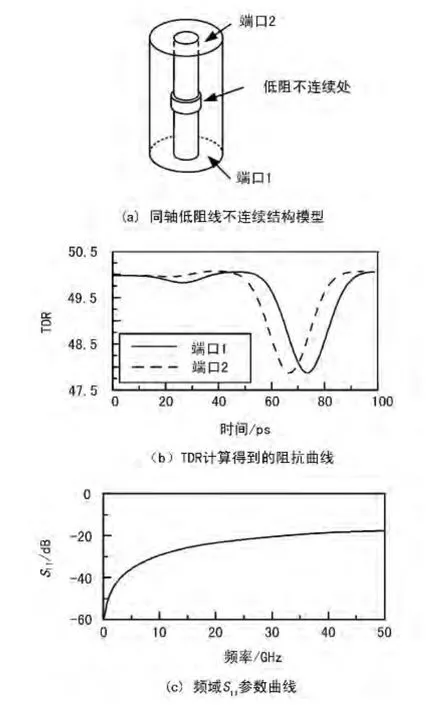
图4 待匹配不连续结构的时域、频域特性
17.52 ps脉宽信号对应的频宽是50 GHz,进一步缩小脉宽可得到更高的时域分辨率,也可得到更为精确的TDR曲线,但这是以更长的计算时间为代价的。为了对上述不连续进行匹配,采用一段同样长1 mm的高阻线临近级联,如图5所示。
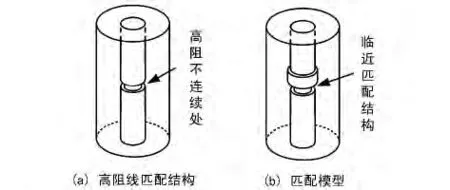
图5 匹配用低阻段和级联后结构
与图5(a)对应的TDR阻抗曲线及频域S11参数曲线分别如图6(a)和6(b)所示。采用简单临近级联,可在低频端起到很好的匹配效果,匹配模型如图5(b)所示,对应的TDR阻抗曲线及频域S11参数曲线如图6(c)和6(d)所示,可见在10 GHz处回波改善了8.64 dB,高频端的匹配则不明显,20 GHz处的回波改善仅为4.1 dB,这是因为寄生效应在高频更为明显,不连续性的电长度明显增加,已不能忽略不计。
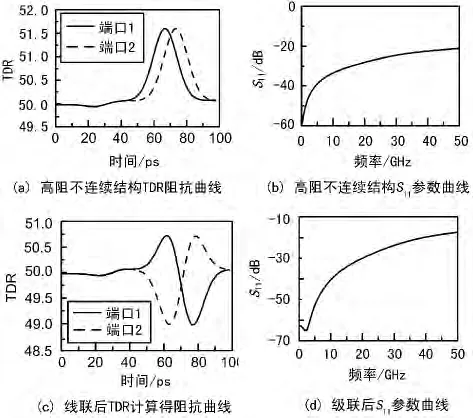
图6 同轴高阻级联匹配效果
2.2 金丝键合的电容补偿
金丝键合是微波、毫米波单元器件及传输线间的一种互联方式,在毫米波频段的使用尤其广泛。然而随着工作频率的不断升高,金丝的趋肤深度不断减小,金丝键合线对电路性能的影响也越来越大,不容忽视。为此,学术界也对金丝键合的特性展开了研究[14]。对多数情况而言,金丝键合在电路中可等效为一个寄生电感,因此,使用多根金丝并联排布,使用更短的键合间距,或者采用更低的金丝拱高,都可有效减小金丝带来的寄生电感,从而减小金丝键合引入的电路性能恶化。然而,这些手段受到微组装工艺条件的限制,不可能无限制的缩小寄生参数;与此同时,还变相提高了装配成本。为了在现有工艺条件下减轻键合对电路性能的影响,可采用附加电容补偿的方式。然而如果不能事先准确评估由金丝键合引入电感的感值,那么这种方式就会存在相当的盲目性。德国CST公司所推出的电磁仿真软件MICROWAVE STUDIO可支持准TEM端口条件下的TDR仿真计算,可以用于对金丝键合电容补偿进行定量化的评估和优化。单根金丝在MICROWAVE STUDIO中的仿真模型和计算结果如图7所示。其中,图7(a)为仿真模型,包括金丝、金丝的微带引出线、计算区域的外部边界,以及激励波端口;图7(b)为仿真计算得到的TDR阻抗曲线;图7(c)则是通过CST时域仿真结果进行傅里叶变换所得到的 S参数曲线。可以看出,尽管CST的MICROWAVE STUDIO与ANSYS的HFSS在不同的求解域求解,但通过后处理均可得到相似的结果形式。
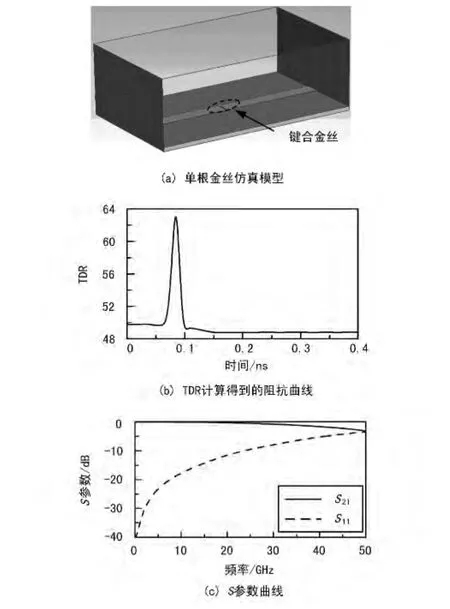
图7 金丝键合模型及仿真曲线
临近电容补偿的模型如图8(a)所示,相应TDR阻抗曲线和S参数如图8(b)和图8(c)所示。可以看出,在20 GHz以下频段,单根金丝引入的不连续性得到了极大改善,在20 GHz点频上,回波的改善达到了12.18 dB。
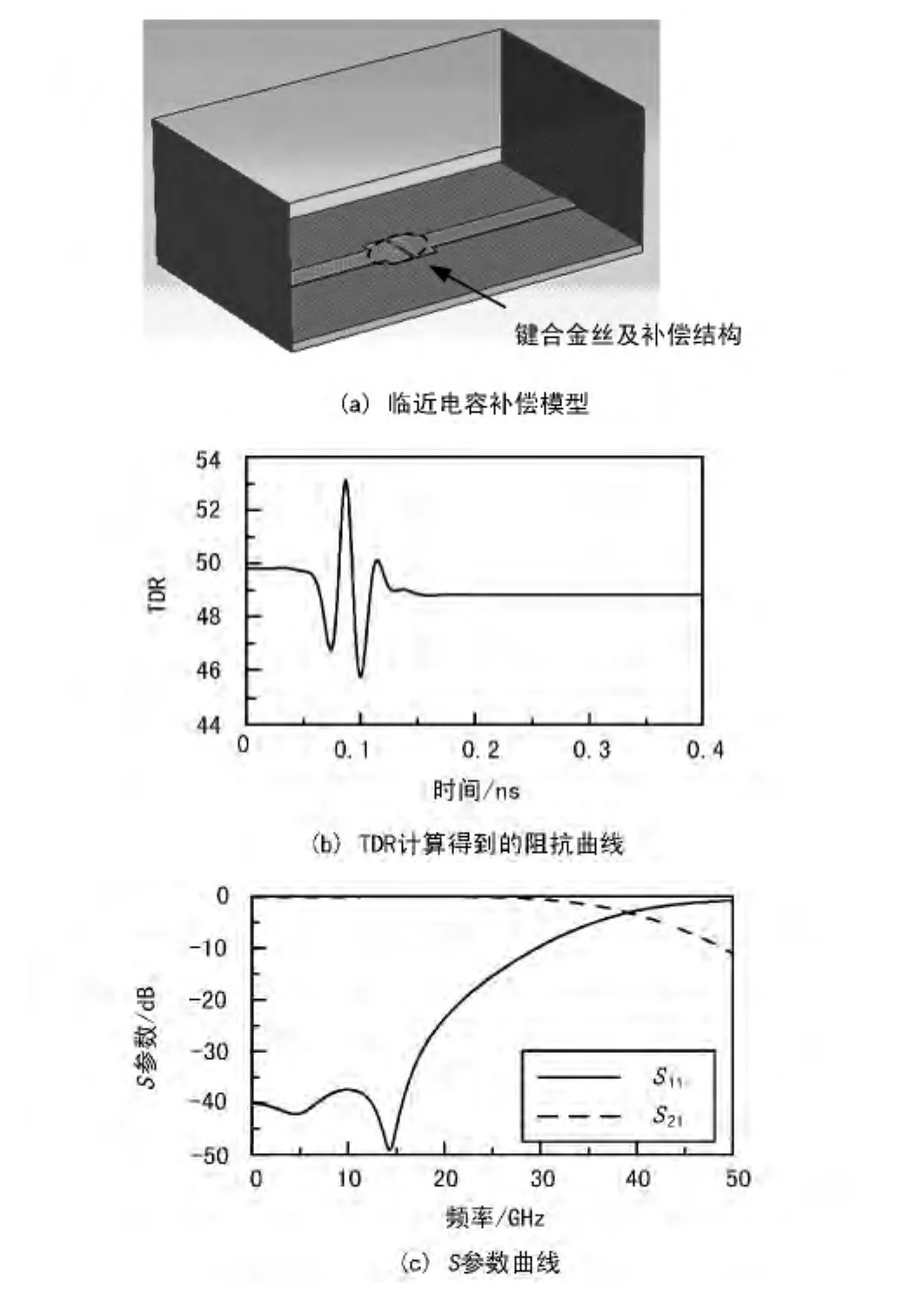
图8 临近电容补偿模型及仿真曲线
3 结束语
TDR作为一种经典微波测量方法,有丰富的理论和经验积淀,在微波电路仿真中起到了不可忽视的作用,已在某些方面显著减轻了设计师的负担。本文所提供的实例说明了TDR在阻抗匹配及金丝键合的电容补偿中起到的作用,但TDR的意义远不止于此。文中的讨论仅限于TEM和准TEM系统,通过使用窄带脉冲作为激励信号并进行一定的后处理,可将TDR概念引入波导这样的非TEM系统。此外,TDR仿真还可与TDR的测试结果相结合,为微波电路的设计和调试带来更大便利。
[1] 索姆洛 P I,亨特J D.微波阻抗测量[M].北京:人民邮电出版社,1990.
[2] 汤世贤.微波测量[M].北京:国防工业出版社,1981.
[3] 严 简.借助时域反射技术检测集成电路的连通性[J].电子测试,2001(1):4 -196.
[4] 李 禾.现代网络测量综述[J].信息技术与标准化,2003(3):9-12.
[5] 袁欢欣,苏藩春.论高精度特性阻抗板的工程设计、制程控制与测试技术[J].印制电路信息,2010(S1):542-550.
[6] 秦 庚,邬宁彪,李小明.印制电路板特性阻抗的测试技术[J].印制电路信息,2004(11):55-57.
[7] DUMBELL K D.Tdr for Microwave Circuits[C]∥ Asia-Pacific Microwave Conference,Adelaide,Australia,1992:361-364.
[8] 刘金凤,邓世文.基于MSA的TDR特性阻抗测试仪性能分析[J].印制电路信息,2012(S1):480-488.
[9] 闫 龙,赵熙东.终端短路式交指带通滤波器的仿真与实现[J].无线电通信技术,2011,37(3):39 -40,50.
[10]谢 军.电子对抗组网仿真技术研究[J].无线电工程,2011,41(4):56 -58,61.
[11]徐兴福.ADS2008射频电路设计与仿真实例[M].北京:电子工业出版社,2011.
[12]刘 余.微波平面时域和频域测试技术研究[D].成都:电子科技大学,2011.
[13]杨国敏.非均匀传输线特性重构及噪声影响分析[D].上海:上海交通大学,2006.
[14]贾世旺,黄笑梅,张中海.EHF频段键合线分析[J].无线电工程,2010,40(4):57-61.
