趋势平稳过程与单位根过程的趋势特征研究

左秀霞

（江苏大学 财经学院，江苏 镇江212013）

一、引 言

趋势是时间序列的重要特征。时间序列的趋势分为确定性时间趋势和随机性趋势两种类型。趋势平稳序列只有确定性时间趋势，没有随机性趋势；而另一类时间序列——差分平稳序列（序列存在单位根）则既有随机性趋势，也可能存在确定性时间趋势。在判断一个序列是趋势平稳还是差分平稳的序列平稳性检验中，需要考虑序列的确定性时间趋势。这需要首先明确趋势平稳序列和差分平稳序列的确定性时间趋势特征。因此，研究趋势平稳序列和差分平稳序列各自的确定性时间趋势特征，就成为检验序列平稳性的一个关键问题。

在序列的平稳性检验中，很多学者针对宏观经济序列中确定性时间趋势的非线性特征展开了研究。一部分学者是从结构突变的角度进行了分析，最突出的是Perron的开创性工作。Perron最先在PP等（半）参数单位根检验中允许确定性时间趋势部分存在结构突变，提出了确定趋势部分带结构突变的单位根检验理论，并对美国的宏观经济数据进行了分析［1－2］。此外，也有学者对确定时间趋势部分存在结构突变的KPSS和Breitung等非参数单位根（平稳性）检验的相关理论进行了研究［3－5］。

另一部分学者则是从高次趋势的角度研究了宏观经济数据的非线性时间趋势特征。王少平分析了1978－1998年中国实际GNP的时间趋势特征，认为GNP具有二次趋势。先退化了数据中的二次趋势，然后对退化趋势后的数据进行了单位根检验，认为退化二次趋势的数据是平稳过程［6］。胡少东等对1952－2006年台湾的实际GDP进行了分析，认为其服从带结构突变和二次趋势的趋势平稳过程［7］。Cuestas等分析了19个国家1870－2003年人均实际GDP的平稳性，发现7个国家的数据具有非线性和高次趋势特征。作者先退化了这7个国家数据中的三次趋势，然后对退化趋势后的数据采用Kapetanios等人的平滑转换的单位根检验进行了分析，发现除法国之外6个国家的数据都是平稳序列［8－9］。

上述研究都是先退化数据中的高次趋势，然后对退化趋势后的数据进行检验和进一步分析。但数据经过退化趋势处理后，在进行检验时，检验统计量的渐近分布已经发生了变化，所以不能再采用传统检验中的临界值进行检验。然而，直接针对具有高次趋势特征序列的单位根（平稳性）检验的研究却屈指可数，只有Busetti和Taylor在分析结构突变的KPSS平稳性检验中，允许确定性趋势部分含高次趋势［4］。

由上述分析可见，要检验具有高次趋势特征序列的平稳性，就需要对带高次趋势的单位根（平稳性）检验的相关理论进行研究，而这又首先需要明确高次趋势平稳过程和带高次趋势的单位根过程各自对应的确定性时间趋势特征。在此基础上，才能够对含高次趋势特征序列的相关收敛性质进行推导。

本文先对高次趋势平稳过程和带高次趋势的单位根过程的概念及其时间趋势特征分别进行研究，然后讨论序列时间趋势特征的确定方法，为分析带高次趋势的单位根（平稳性）检验的相关理论打好基础。

二、高次趋势平稳过程的趋势特征

白噪声过程是最特殊的平稳过程，该过程围绕0上下波动，并且在每一时刻的取值完全随机，不受前面时刻取值的影响。其定义如下：

白噪声过程是最基本的平稳过程，任何平稳或非平稳的随机过程都是由白噪声过程经过构造而生成。

（一）无确定部分的平稳过程

与白噪声过程不同，一般平稳过程在前后时刻的取值是相关的，下面将给出无确定部分的一般平稳过程的定义。

（二）带截距的平稳过程

如果平稳过程不是围绕0，而是围绕某个常数上下波动，则是带截距的平稳过程。

定义3：设｛εt｝是高斯白噪声过程，ut＝ψ（L）εt，t＝1，2，…是平稳过程，那么：

（三）线性趋势平稳过程

若趋势平稳过程不是围绕0或某个常数上下波动，而是具有某种随时间变化的线性趋势，则是线性趋势平稳过程。

（四）高次趋势平稳过程

如果趋势平稳过程具有随时间变化的高次趋势特征，则是高次趋势平稳过程。

定义5：设｛εt｝是高斯白噪声过程，ut＝ψ（L）εt，t＝1，2，…是平稳过程，那么：

三、带高次趋势的单位根过程的趋势特征

在单位根过程中，最特殊的是随机游走。该过程在任意两个时刻间的变化都是完全随机的，不受前面时刻取值和时刻间变化的影响。其定义如下：

定义6：设｛εt｝是高斯白噪声过程，那么称

可见，随机游走是由白噪声构成的部分和过程，其波动不具有稳定性。

（一）不带确定部分的单位根过程

与随机游走不同，一般单位根过程的增量过程通常存在自相关，下面将给出不带确定部分的单位根过程的定义。

定义7：设｛εt｝是高斯白噪声过程，ut＝ψ（L）εt，t＝1，2，…是平稳过程，那么：

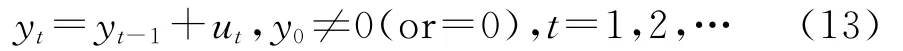
是不带确定部分的单位根过程，并称ut是构成单位根过程yt的增量过程［10］435－436。

由式（13）整理得：

可见，不带确定部分的单位根过程是由平稳过程构成的部分和过程。不带确定部分的单位根过程在任意两个时刻间的变化不再是完全随机的，而是与前面时刻间的变化相关。

随机游走是一种典型的随机性趋势，而由一般平稳过程构成的部分和过程，即不带确定部分的单位根过程，也可通过BN分解将其分解为一个随机游走和一个周期部分［11］。可见，不带确定部分的单位根过程含有随机性趋势。

（二）带漂移的单位根过程

若单位根过程具有某种随时间变化的线性趋势，则是带漂移的单位根过程。

定义8：设｛εt｝是高斯白噪声过程，ut＝ψ（L）εt，t＝1，2，…是平稳过程，那么：

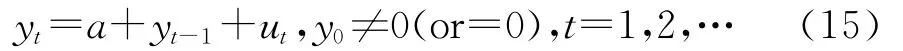
是带漂移的单位根过程，并称ut是构成单位根过程yt的增量过程。

由式（15）整理得：

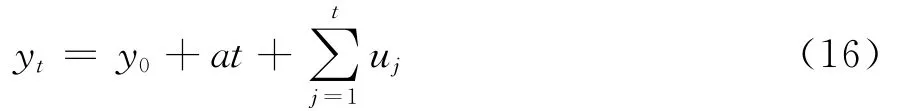
可见，带漂移的单位根过程是由关于时间t的线性函数和由平稳过程构成的部分和过程组合而成。因此，带漂移的单位根过程既有随时间变化的线性趋势特征，也有随机性趋势特征。

（三）带线性趋势的单位根过程

如果单位根过程具有随时间变化的二次趋势特征，则是带线性趋势的单位根过程。

定义9：设｛εt｝是高斯白噪声过程，ut＝ψ（L）εt，t＝1，2，…是平稳过程，那么：

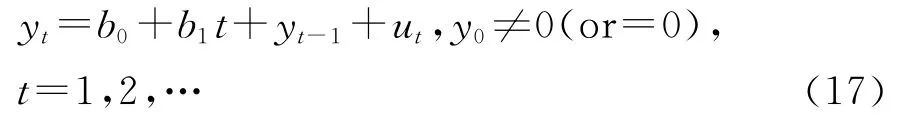
是带线性趋势的单位根过程，并称ut是构成单位根过程yt的增量过程。

由式（17）整理得：

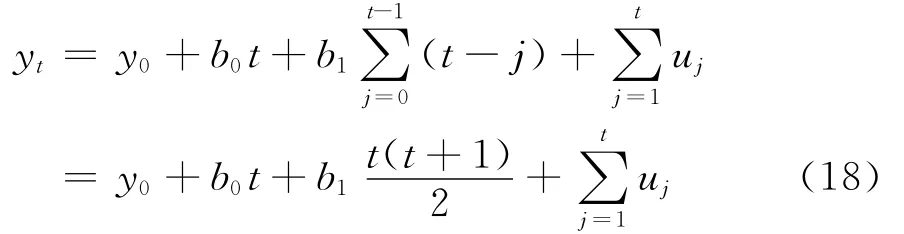
可见，带线性趋势的单位根过程是由关于时间t的二次函数和由平稳过程构成的部分和过程组合而成。因此，带线性趋势的单位根过程既有随时间变化的二次趋势特征，也有随机性趋势特征。

（四）带高次趋势的单位根过程

如果单位根过程具有随时间变化的k＋1（k≥2）次趋势特征，则是带k（k≥2）次趋势的单位根过程。

定义10：设 ｛εt｝是高斯白噪声过程，ut＝ψ（L）εt，t＝1，2，…是平稳过程，那么：

yt＝b0＋b1t＋b2t2＋…＋bktk＋yt－1＋ut，y0≠0（or＝0），t＝1，2，… （19）

是带k（k≥2）次趋势的单位根过程，并称ut是构成单位根过程yt的增量过程。

由式（19）整理得：

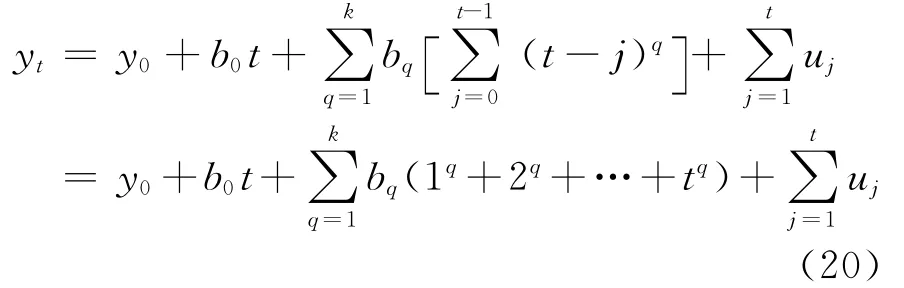
可见，带k（k≥2）次趋势的单位根过程是由关于时间t的k＋1次函数和由平稳过程构成的部分和过程组合而成。因此，带k（k≥2）次趋势的单位根过程既有随时间变化的k＋1次趋势特征，也有随机性趋势特征。

由以上分析可见，由于单位根过程中一阶滞后项系数ρ＝1，从而使t时刻以前yt中的信息全部保留下来，因此yt中的时间趋势也全部保留下来。这样，经过叠加使得带漂移的单位根过程所含的时间趋势特征实际是线性趋势，带线性趋势的单位根过程所含的时间趋势特征实际是二次趋势，带k（k≥2）次趋势的单位根过程所含的时间趋势特征实际是k＋1次趋势。此时，yt中含有两种趋势：确定性趋势和随机性趋势。

四、时间趋势特征的确定

通过前面分析，可以确定k（k≥1）次趋势平稳过程和带k（k≥1）次趋势的单位根过程分别具有k次和k＋1次时间趋势特征。然而，如何根据图形确定一个趋势平稳过程或单位根过程的时间趋势特征呢？

差分变换不仅可以将一个单位根过程变成一个（趋势）平稳过程，即消除序列的随机性趋势，而且还可以降低序列的确定性时间趋势特征。如果一个序列yt含有k＋1（k≥0）次时间趋势，那么序列的确定部分是关于时间t的k＋1次多项式，并且tk＋1项的系数c不为0。那么对yt一阶差分后，原序列中的c·tk＋1项变为：

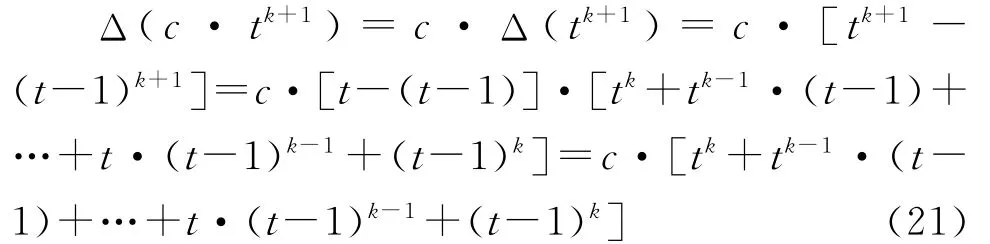
式（21）中t的最高次项是（k＋1）c·tk项。因此，差分序列的确定性时间趋势部分中t的最高次项是tk项，即差分一次可以使时间序列的趋势特征降低一阶。以此类推，差分m次就可以使序列的趋势特征降低m阶。

由此可见，对一个时间序列，无论是趋势平稳还是单位根，都可以通过差分来确定其时间趋势特征。具体而言，如果一个序列经过至少m次差分才可以消除其时间趋势特征，或如果一个序列经过m－1次差分后具有随时间变化的线性趋势特征，那么该序列具有m次时间趋势特征。

五、结论和进一步研究

为了研究具有高次趋势特征序列的单位根检验问题，本文对高次趋势平稳过程和带高次趋势的单位根过程的时间趋势特征分别进行了讨论和分析。通过研究发现，一阶滞后项系数的绝对值小于1使得（趋势）平稳过程在每一时刻的包括时间趋势在内的所有信息都只有一部分被保留下来，因此经过叠加就使k（k≥0）次（趋势）平稳过程具有k（k≥0）次趋势特征。而一阶滞后项系数等于1使得单位根过程在每一时刻的包括时间趋势在内的所有信息全部保留下来，因此经过叠加使带漂移的单位根过程实际具有线性趋势特征，带k（k≥1）次趋势的单位根过程具有k＋1次趋势特征，并且yt中此时含有确定性趋势和随机性趋势两种趋势。分析还发现，无论是趋势平稳还是单位根过程，都可以通过差分变换确定其时间趋势特征。

明确了趋势平稳过程和单位根过程的时间趋势特征，对于具有k＋1次时间趋势特征的序列｛yt｝的单位根检验问题还有待进一步研究。

［1］ Perron P．The Great Crash，the Oil Price Shock，and the Unit Root Hypothesis［J］．Econometrica，1989，57（6）．

［2］ Perron P．Testing for A Unit Root in a Time Series with A Changing Mean ［J］．Journal of Business ＆ Economic Statistics，1990，8（2）．

［3］ Lee J，Huang C J，Shin Y．On Stationary Tests in the Presence of Structural Breaks［J］．Economics Letters，1997（2）．

［4］ Busetti F，Taylor A M R．Variance Shifts，Structural Breaks，and Stationarity Tests ［J］．Journal of Business ＆Economic Statistics，2003，21（4）．

［5］ Belaire－Franch J，Contreras D．Nonparametric Unit Root Test and Structural Breaks［J］．Journal of Time Series Econometrics，2011，3（2）．

［6］ 王少平．我国实际GNP的时间趋势与周期演变［J］．经济研究，1999（7）．

［7］ 胡少东，李非．台湾GDP序列结构突变与经济周期［J］．台湾研究集刊，2009（3）．

［8］ Cuestas J C，Garratt D．Is Real GDP Per Capita A Stationary Process？Smooth Transitions，Nonlinear Trends and Unit Root Testing［J］．Empirical Economics，2011，41（3）．

［9］ Kapetanios G，Shin Y，Snell A．Testing for A Unit Root in the Nonlinear STAR Framework［J］．Journal of Econometrics，2003，112（2）．

［10］Hamilton J D．Time Series Analysis［M］．Princeton：Princeton University Press，1994．

［11］Beveridge S，Nelson C R．A New Approach to Decomposition of Economic Time Series into Permanent and Transitory Components with Particular Attention to Measurement of The‘Business Cycle’［J］．Journal of Monetary Economics，1981，7（2）．