基于密度的面板数据聚类分析

杨 娟，谢远涛

（1．中国人民大学 统计学院，北京100872；2．对外经济贸易大学 保险学院，北京100029）

一、引 言

面板数据分析是计量经济学的一个重要组成部分，主要研究集中于混合模型、分层模型等领域，而面板数据的聚类分析研究还处于发展阶段，数据挖掘中经典聚类分析方法主要适用于截面数据的聚类。面板数据聚类主要讨论两类问题：如何度量数据对象的相似性以及采用何种聚类方法。度量相似性的方法分为两种：距离和相似系数。主要的聚类方法可以划分为五大类：基于划分的、基于密度的、基于层次的、基于模型的和基于方格的，当然还存在其他类型的聚类方法［1］184－188。

（一）构造相似性度量

Bonzo等基于概率连接函数来定义相似系数，采用改进的自适应模拟退火－遗传算法优化目标函数［2］。Nie将不同时期的观测给予不同权重，构造距离函数［3］。朱建平等将单指标面板数据转化为截面数据做聚类分析［4］。张可等根据指标的几何特征，用扩展灰色关联度矩阵构造相似矩阵［5］。任娟等用自适应滑动窗口分段方法提取面板数据中时序局部变化的形状特征［6］。杨毅等用主成分分析提取面板数据指标的特征，对面板数据进行有序聚类分析［7］。李因果等用“绝对指标”、“增量指标”和“波动指标”构造综合距离函数，使用专家调查法和熵权系数法确定距离函数的参数，该方法适用于经济领域的面板数据聚类［8］。吴利峰等根据面板数据的凸性，提出用三维灰色凸关联度构造相似矩阵，这两类方法适用于计算机控制和图形处理领域的面板数据聚类［9］。

上述文献计算新的相似性度量时，根据面板数据的数字特征、形状特征、动态特征等构造相似性度量，只提取了面板数据的部分特征，适用于特定数据类型的面板数据和聚类目的。

（二）聚类方法

De la等提出了基于模型的多水平面板数据聚类方法，所用模型为混合非线性分层模型［10］。Juárez等提出基于模型的面板数据聚类方法，使用偏态厚尾的T分布的自回归模型，根据数据的动态特征、均衡水平、协方差来聚类［11］。Bonzo等使用了基于层次的聚类方法。Nie等使用基于密度的应用噪声的空间聚类方法（DBSCAN）。杨毅等用费希尔最优化求解法，重新定义了类间距离和损失函数，讨论了面板数据的有序聚类问题。

上述文献中，基于模型的聚类方法的优点是：能够处理噪音数据，具有可解释性和实用性。不足之处：不能处理各种分布的面板数据，需要根据数据的分布和一定的假设条件进行模型的设定，需要设定分类的个数，聚类效果对参数设定很敏感。基于层次的聚类方法需要事先确定类的个数。基于密度的应用噪声的空间聚类方法（DBSCAN）需要确定两个参数。

本文的创新之处：根据Logistic回归模型，利用面板数据的各个指标和整体特征构造相似性度量，计算两两数据对象的相似系数，构造非对称相似矩阵。针对非对称相似矩阵，提出采用最佳优先搜索和轮廓系数的BF－DBSCAN①Best－First Search，Density Based Spatial Clustering of Application with Noise，缩写为BF－DBSCAN。Best－First Search，Density Based Spatial Clustering of Application with Noise，缩写为BF－DBSCAN。面板数据聚类方法。

二、用Logistic回归构造相似系数

面板数据用Xi（t）m表示，数据对象总数为N，每个数据对象包含T个样本和M个指标或变量，其中i＝1，2，…，N；t＝1，2，…，T；m＝1，2，…，M。任意数据对象i，其样本记为i（t）。例如，全国2000—2011年的发展指标，北京市（数据对象i）第m个指标记为xim，所有指标记为xi；北京2011年（样本i（2011））第m个 指 标 记 为xi（2011）m，所 有 指 标 记为xi（2011）。

（一）Logistic回归模型

Fisher于1919年提出Logistic回归模型，1972年Nelder和Wedderburn首次提出广义线性模型的概念，Logistic回归模型是广义线性模型的一种特例，响应变量服从Bernoulli分布。

用Logistic回归构造相似系数，将数据对象j的所有样本看作一类，记作类Cj；其他数据对象的所有样本看作为另一类，记作类Cj′。构造面板数据的响应变量Y，且Y～Bernoulli（π），响应变量yj＝1，yj′＝0，其中j≠j′。

样本i（t）属于类Cj的概率为πi（t），其中i、j＝1，2，…，N。πi（t）与i（t）的指标xi（t）有关，因此πi（t）＝Pr （yi（t）＝1｜yj＝1，xi（t）） ，其中yi（t）＝1表示i（t）属于类Cj，πi（t）表示条件概率。

（二）构造相似系数和非对称相似矩阵

定义1：给定yj＝1和xi（t）的条件下，i（t）与j的相似系数记为s（i（t），j），s（i（t），j）为条件概率，即有s（i（t），j）＝πi（t）＝Pr （yi（t）＝1｜yj＝1，xi（t））。

定义2：向量S（i（t），j）表示j和i所有样本i（t）的相似系数。

定义3：给定yj＝1和xi的条件下，i与j的相似系数记为s（i，j），即s（i，j）＝f（S（i（t），j））。

计算相似系数s（i，j）的核心是确定函数f（·）。函数f（·）可以定义为取最大值、最小值、均值、中位数等。如果数据对象内部结构相似，而且数据对象之间分离较远，采用不同的函数f（·），聚类结果差别不大。但是，如果数据对象之间分离得不够好，或存在异常点，或不是球形，或数据对象的样本分布不够均匀，采用不同的函数f（·），聚类结果差别将很大，具体论证参见Goldstein等的论文［12］。

还需要说明s（i，j）≠s（j，i），即两两数据对象的相似系数是不对称的。给定数据对象j，i与j相似的系数为s（i，j）＝f（S（i（t），j））。给定数据对象i，j与i相似系数为s（j，i）＝f（S（j（t），i））。由于S（j（t），i）和S（i（t），j）是条件概率组成的列向量，因此s（i，j）≠s（j，i）。

定义4：非对称相似矩阵Φ是一个N维方阵，一般s（i，j）≠s（j，i）。

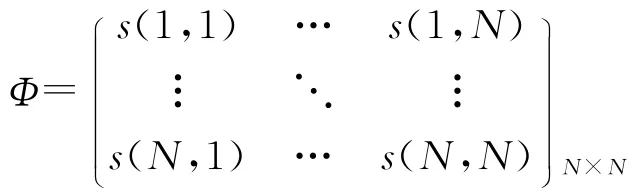
根据以上定义，用Logistic回归模型计算非对称相似矩阵的具体过程如下：

输入：面板数据Xi（t）m。

输出：非对称相似矩阵Φ。

步骤1：构造面板数据的响应变量Y，Y～Bernoulli（π），yj＝1，yj′＝0，其中j≠j′，j＝1，2，…，N；

步骤2：用Logistic回归模型计算i（t）和j的相似系数s（i（t），j），进一步，确定函数f（·），计算i和j的相似系数s（i，j）；

步骤3：循环执行以上步骤，直到每个数据对象的响应变量都曾经被设置为1，或者直到所有相似系数s（i，j）组成非对称相似矩阵Φ。

三、面板数据的聚类方法

（一）DBSCAN聚类方法

1996年 DBSCAN（Density Based Spatial Clustering of Application with Noise）方法由Ester等提出，它是一种典型的基于密度的聚类算法［13］226－231。DBSCAN方法的基本思想是：数据对象i和j为同一族的条件是i和j是密度相连的。数据对象是噪音的条件是该数据对象到任何一个其他数据对象都不密度相连。

给定数据对象i和参数ε，以i为圆心，以ε为半径画圆，该圆范围内的数据对象为i的ε邻域。

给定参数MinPts，如果i的ε邻域内包含数据对象的个数大于等于MinPts，则称i为核心对象，如果i的ε邻域内包含数据对象的个数小于MinPts，称i为边界对象。

直接密度可达的定义：给定数据集，如果i是一个核心对象，且j在i的ε邻域内，则i到j直接密度可达。密度可达的定义：给定数据对象k1，k2，…，kN，任意数据对象ki，其中i＝1，2，…，N，存在ki到ki＋1直接密度可达，则称k1到kN密度可达。密度相连的定义：对象集合中存在一个数据对象k，如果k到数据对象i和j密度可达，则称数据对象i和j密度相连。所有密度相连的数据对象的集合称为族。DBSCAN方法的过程为：

输入：横截面数据集，参数ε和MinPts。

输出：聚类结果。

步骤1：从任意数据对象i开始，通过宽度优先（breadth－first）搜索所有与i密度可达的数据对象，如果数据对象i是核心对象，将它们记为同一族。如果数据对象i是边界对象，就将之记为噪音，直到找到一个完整的族；

步骤2：随机选取一个新的数据对象i′进行处理，得到下一个族。算法一直进行下去，直到所有的数据对象都被标记过为止。

目前经典的聚类方法都是基于对称的相似矩阵，不适用于非对称的相似矩阵。对于非对称相似矩阵，DBSCAN聚类方法从任意一个核心对象j开始，如果i到j直接密度可达，那么i和j为同一族。但是，如果从核心对象i开始，由于相似系数s（i，j）≠s（j，i），不一定有j到i直接密度可达，那么i和j不在同一个族。因此用DBSCAN方法分析非对称相似矩阵，如果从任意的核心对象开始，每次分析得到的聚类结果将不相同。因此，不能选择任意的数据对象作为核心对象，为了解决这个问题，本文提出了基于最佳优先搜索和轮廓系数的BF－DBSCAN聚类方法，用R语言编程实现。

（二）最佳优先搜索

启发式搜索（heuristic search）利用问题自身的某些特征信息来指导搜索过程，可以大大减少搜索空间，提高搜索的效率。本文采用一种启发式算法——最佳优先搜索算法对DBSCAN方法进行改进，命名为BF—DBSCAN。

最佳优先搜索（best－first search）算法的基本原理是，根据启发评估函数的计算结果，总是选择代价最小的那条路径向下搜索。在搜索过程中通过不断地放弃代价较大的路径，从而最终找到代价最小的问题求解答案，朝着最有希望的方向前进，加快问题的求解过程。评估数据对象重要性的函数称为启发评估函数，一般形式为：w（j）＝g（j）＋h（j）。g（j）是从任意数据对象j开始，到起始对象的路径实际长度，h（j）是数据对象j到目标距离的启发性估计［14］93－107。

（三）轮廓系数

1990年Kaufman提出轮廓系数（Silhouette Coefficient）从族内部结构的紧密型和族间结构的可分性这两个方面对聚类有效性进行分析，用于确定最优聚类数和聚类质量评价［15］108－117。和其他的聚类有效性函数相比较，轮廓系数具有良好的评价能力，得到广泛应用［16］。为了更好地分析非对称相似矩阵，本文用轮廓系数来评价数据对象j内部样本结构的紧密性，以及j和其他数据对象间的可分性。

（四）BF—DBSCAN聚类方法

定义5：启发评估函数w（j）＝g（j）＋h（j），令g（j）＝0，h（j）＝SCj，其中SCj为数据对象j的轮廓系数。

轮廓系数取值为－1和1之间，其值越大表示数据对象作为单独一类的质量越好。对于非对称相似矩阵，DBSCAN方法从任意对象开始搜索，会增加很多的搜索空间，因此令h（j）＝SCj，计算每个数据对象的SCj值，按照SCj降序进行排序，将内部紧密性和类间可分性最好的数据对象排在最前面，优先选取直接密度可达的数据对象，极大地减少了原来DBSCAN的搜索空间。

BF—DBSCAN方法的基本思路是：按照启发评估函数值的大小，从启发函数值最大的数据对象j开始扩展。如果j是核心对象，且与i是直接密度可达的，那么j和i属于同一个族；如果j为边界对象，那么j为一个噪音。然后按照启发函数值从大到小的顺序，处理下一个数据对象。直到每个数据对象都被标记过为止。所有密度相连的数据对象为同一族。

如果聚类分析的目的是为每一个数据对象找到相应的族，在噪音的处理上，通过确定每个族的中心点，那么噪音数据对象就属于离它最近的族。如果聚类的目的是找出噪音数据，就不必对噪音进行任何处理。面板数据聚类的步骤如下：

输入：面板数据，参数ε和MinPts。

输出：聚类结果。

步骤1：用Logistic回归模型计算两两数据对象相似系数，组成非对称相似矩阵Φ；

步骤2：计算SCj的值，按照SCj的降序排列每个数据对象的优先次序，记为Φ′＝ ｛1，2，…，N｝；

步骤3：在相 似矩阵Φ′＝ ｛1，2，…，N｝中，从SCj最大的数据对象j开始，如果j是核心对象，在ε邻域内搜索所有与j直接密度可达的数据对象，记为同一个族；如果j是边界对象，则记为噪音；

步骤4：按照SCj降序处理下一个数据对象，所有密度相连的数据对象的集合为同一族。算法一直进行下去，直到所有的数据对象都被标记过为止；

步骤5：噪音的处理。计算每个族的中心点，噪音数据对象属于离它最近族。直到所有噪音数据对象都被标记过为止。

四、实例分析

采用中国人民大学数据与调查中心编制的中国发展指数（RCDI），从2005年到2011年，共31个省份的四个分指数：健康指数X1、教育指数X2、生活指数X3和经济指数X4。我们从三个方面考察BF—DBSCAN聚类结果的有效性：首先，比较面板数据聚类结果和截面数据聚类结果；然后，比较DBSCAN和BF—DBSCAN的聚类结果；最后，比较参数ε的设置对BF—DBSCAN聚类结果的影响。

（一）比较BF－DBSCAN和DBSCAN的聚类结果

表1 比较BF－DBSCAN和DBSCAN的聚类结果表

根据该面板数据的形状，f（·）取最大值，参数ε＝0．17和 MinPts＝1，计算得到非对称相似矩阵Φ，分别使用BF—DBSCAN和DBSCAN方法，聚族结果如表1所示。同BF—DBSCAN的聚类结果相比较，如果从不同的数据对象开始，每次DBSCAN方法得到的聚类结果不相同，例如，从任意数据对象i开始的DBSCAN方法，在第V族中，山东和西藏等省份在一起。然而，从任意数据对象j开始的DBSCAN方法，将山东和甘肃、天津等省份分在第III族，将甘肃和天津分为一族，这样的聚类结果显然是不合理的。因此，基于Logistic回归计算的非对称相似矩阵，不能直接使用经典的DBSCAN聚类方法，使用BF—DBSCAN方法，可以得到合理的聚类结果。

（二）参数对BF—DBSCAN聚类结果的影响

使用Logistic回归模型，当f（·）取最大值，MinPts＝1，参数ε取不同值时，BF—DBSCAN聚类结果如表2所示。ε取不同值，第I、II、VI族的聚类结果完全相同，ε的值越大，噪音数据对象越多，族的划分越细，其中ε＝0．17聚类结果较好。BF—DBSCAN和DBSCAN面临同样的问题，不同的参数设置对聚类结果较敏感，因此BF—DBSCAN方法聚类具有一定的灵活性，需要调整参数，才能得到理想的聚类结果。

表2 参数ε取不同值的BF－DBSCAN聚类结果表

（三）比较BF—DBSCAN聚类结果和截面数据聚类结果

根据历年发布的中国发展指数的聚类结果，见表1和表3中BF—DBSCAN的聚类结果。从2005年、2008年及2011年中国发展指数的聚类结果来看①2005年聚类结果参见《中国发展指数的编制研究》，中国人民大学学报2007年第2期；2008年聚类结果参见《中国发展指数（2008）编制成果研究》，中国人民大学学报2009年第1期；2011年聚类结果参见彭非等人著作第136～137页。，中国31个省份主要分为四大类，其中第一类的始终没有变化，只有北京和上海。第二类的变化不大，其中天津、浙江、江苏、广东一直稳居第二类，但是福建、辽宁、吉林在2011年下降到第三类，山东从2005年的第三类上升到2011年的第二类。第三类中省份越来越多，第四类中省份越来越少，其中新疆从2005年和2008年的第三类下降到2011年的第四类，重庆、海南、广西、宁夏、江西、四川、安徽从2005年的第四类上升到2011年的第三类，说明中国中西部地区发展速度较快，中西部省份与东部省份的发展差距逐年缩小。

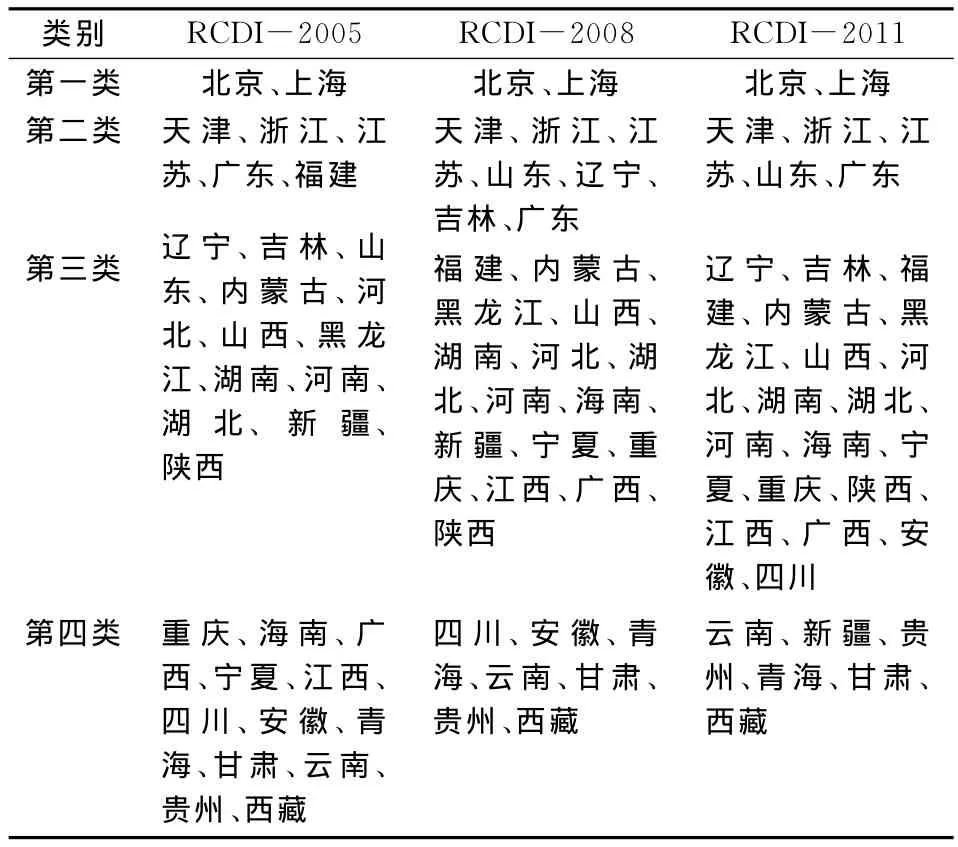
表3 RCDI－2005、2008、2011年聚类结果比较表

从BF—DBSCAN的聚类结果来看，如表1中第二列所示，将31个省份划分为6大类，第I类对应截面数据聚类的第一类，只有北京和上海；第IV类对应第二类；第III类对应第三类；第V类对应第四类；而第II类的海南、广西，第VI类的新疆和陕西难以确定类别。由于海南和广西、新疆和陕西发展速度的波动幅度较大，处于一种发散的状态，因此它们处于第三类和第四类之间。

比较BF—DBSCAN和截面数据的聚类结果，矛盾点在于：在BF—DBSCAN中，天津被划分为第三类，而内蒙古、河北被划分为第二类。在截面数据聚类中，天津始终被划分为第二类，内蒙古、河北被划分为第三类。由于天津、内蒙古和河北综合发展速度处于上下波动的的状态，因此在BF—DBSCAN聚类结果中，天津和第三类省份比较接近，内蒙古、河北和第二类省份比较接近。

综上所述，比较BF—DBSCAN聚类结果和截面数据聚类结果，说明了BF—DBSCAN聚类结果的合理性，充分反映了7年来中国31个省份发展指数变化的综合情况。

五、结 论

用Logistic回归计算相似系数，能够充分利用面板数据的各个指标，从整体上得到两两数据对象的相似系数和非对称相似矩阵。对于非对称相似矩阵，提出BF—DBSCAN聚类方法。实例分析表明，相对于DBSCAN，BF—DBSCAN方法的聚类结果较为理想，由于Logistic回归模型适合分类变量和连续变量，因此BF—DBSCAN方法也适用于分类变量和连续变量的面板数据。同DBSCAN方法一样，BF—DBSCAN方法不需要事先确定族的个数，对参数的设置比较敏感。因此，基于密度的面板数据聚类方法具有较好有效性和实用性。

［1］ 王珊，李翠平，李盛恩，等．数据仓库与数据分析教程［M］．北京：高等教育出版社，2012．

［2］ Bonzo D C，Hennoeilla A Y．Clustering Panel Data Via Perturbed Adaptive Simulated Annealing and Genetic Algorithms［J］．Advances in Complex Systems，2002，5（4）．

［3］ Nie G，Chen Y，Zhang L，Guo Y．Credit Card Customer Analysis Based on Panel Data Clustering［J］．Procedia Computer Science，2010（1）．

［4］ 朱建平，陈民恳．面板数据的聚类分析及其应用［J］．统计研究，2007（4）．

［5］ 张可，刘思峰．灰色关联聚类在面板数据中的扩展及应用［J］．系统工程理论与实践，2010，30（7）．

［6］ 任娟，陈圻．基于形状特征的多指标面板数据聚类方法及其应用［J］．统计与信息论坛，2011，26（10）．

［7］ 杨毅，赵国浩，秦爱民．面板数据的有序聚类分析及应用——以全球气候变化聚类分析为例［J］．统计与信息论坛，2012，27（7）．

［8］ 李因果，戴翼，何晓群．基于自适应权重的面板数据聚类方法［J］．系统工程理论与实践，2013（2）．

［9］ 吴利峰，刘思峰．基于灰色凸关联度的面板数据聚类方法及应用［J］．系统工程理论与实践，2013（7）．

［10］De la Cruz－Mesía R，Quintana F A，Marshall G．Model－Based Clustering for Longitudinal Data［J］．Computational Statistics ＆Data Analysis，2008，52（3）．

［11］Juárez M A，Steel M F J．Model－Based Clustering of Non－Gaussian Panel Data based on Skew－t Distributions［J］．Journal of Business ＆ Economic Statistics，2010，28（1）．

［12］Goldstein J，Ramakrishnan R，Shaft U．Compressing Relations and Indexes［C］∥Data Engineering，Proceedings，14th International Conference on IEEE，1998．

［13］Ester M，Kriegel H－P，Sander J，Xu X．A Density－Based Algorithm for Discovering Clusters in Large Spatial Databases with Noise［C］∥ Published in Proceedings of 2nd International Conferene on Knowledge Discovery and Data Mining（KDD－96），1996．

［14］Luger G F．人工智能——复杂问题求解的结构和策略［M］．北京：机械工业出版社，2004．

［15］ Kaufman L，Rousseeuw P J．Finding Groups in Data：An Introduction to Cluster Analysis ［M］．New York：Wiley．2009．

［16］Dudoit S，Fridlyand J．A Prediction－Based Resembling Method for Estimating the Number of Clusters in a Dataset［J］．Genome Biology，2002，3（7）．