基于梯度统计量的逆抽样下风险差的置信区间构建

牛翠珍，范国良

（1．中国人民大学 统计学院，北京100872；2．安徽工程大学 数理学院，安徽 芜湖241000）

一、引 言

在流行病学研究中，当所研究的疾病诸如癌症较为稀有时，如果采用普通的二项抽样很难得到感兴趣的个体，则会使基于此的统计推断变得较为复杂，这时便可考虑采用逆抽样方式，也就是负二项抽样［1］。根据这种抽样方案，当抽样直到感兴趣的事件数目达到预先设定的数值时，首先需要确定相互独立的两组中感兴趣的事件发生数目x1和x0的值，其中x1为暴露组中事件发生数目，x0为非暴露组中事件发生数目。在样本选入过程中，样本一个个进入，直到两组中感兴趣的事件发生数目观测值分别为x1和x0后，样本获得过程终止，此时的两组中不感兴趣的事件发生数目分别记为Y1和Y0，通过这种抽样过程获得的样本属于逆抽样过程获得的样本。例如在流行病学研究中，研究某种危险因素是否会导致暴露者与非暴露者患病的风险存在差异，可将暴露者和非暴露者分成两组，以研究这两组中患病率的差异，当这种疾病比较稀有时，考虑采用逆抽样的方式。

为研究基于逆抽样得到的两组独立的样本中患病风险是否相同，有必要进行一些统计推断，如构造置信区间，或是对两组患病风险差进行假设检验。针对这个问题，现有文献已对此有很多研究：Lui提出了优势比的三种简单的置信区间构造方法［2］；进一步，Lui又探讨了相对风险差的条件极大似然估计以及精确检验［3］；Tian等人研究了风险比的WALD、得分以及似然比检验统计量的应用［4］；对于风险差的置信区间构造，Tang等人给出了一种基于得分统计量的渐进方法［5－6］；戴明峰等人通过统计模拟研究表明了polya后验方法构造的置信区间长度较小，并能够很好地覆盖真值［7］。

另一方面，对于参数检验问题，Terrell提出了一种新的检验统计量，这一新的梯度统计量可视之为WALD以及得分统计量的一种巧妙结合，明显优于WALD以及得分统计量，既不需要计算Fisher信息阵也不需要计算其逆矩阵［8］；Lemonte等人认为梯度统计量、似然比统计量、WALD以及得分检验统计量在一阶渐进意义下是等价的，同时没有哪个统计量在二阶局部功效方面一致并更优，因此可以说梯度统计量是其他三种传统统计量的一个有效补充［9］；进一步，Lemonte等人又讨论了存在讨厌参数情形下该统计量的理论性质，还讨论了该统计量在指数族非线性模型以及对称线性模型下的局部功效表现［10－11］。

二、置信区间构建方法

（一）基本符号

（二）已有方法介绍

其中I（Δ，λ）是期望Fisher信息阵。

（三）基于梯度方法的风险比置信区间的构造

在计算中，得分方法、似然比方法、GREMLE以及GREUMVUE都涉及到λ的限制极大似然估计，也就是说需要求解方程 （1）。对于该方程的求解，Lui采用了一种双迭代的方法。Tang等人得出了一种利用复数的非迭代算法来求解该方程，所提出的求解方法比之前的双迭代算法更易操作。但是，这种方法也存在一个问题，因为λ及其估计都必须是正实数，但通过利用复数的非迭代算法得到的结果有可能是一些复根。为了避免这一问题，考虑采用一种由Farrington等人介绍的求解方法［13］。

将方程（1）改写成如下形式的一元三次方程：

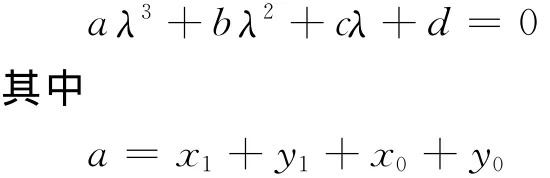
三、蒙特卡洛数值模拟

为研究基于梯度统计量（如GREMLE和GREUMVUE方法）置信区间的模拟表现，从Tang等人的模拟结果看，WALD和UMVUE两种方法构建的置信区间，一般区间宽度较大或是覆盖率较低，因此可考虑比较得分方法、似然比方法和文中提出的两种基于梯度统计量构建的置信区间的数值模拟表现，采用区间覆盖概率（CP）和期望区间宽度（ECW）这两个指标来评价这4种方法构建的置信区间的表现。对于覆盖概率（CP），越接近于预先设定的置信水平，说明该种置信区间构建方法越好。同时，在覆盖概率 （CP）能够较好控制的情况下，ECW越短说明方法越好。

设定x0＝x1＝5，下面给出三种p1和Δ的设置：第 一 种，对 于p1＝0．001 0，考 虑Δ＝－0．000 5，－0．000 1，0，0．000 1，0．000 5；第 二种，对于p1＝0．050，考虑Δ＝－0．025，－0．005，0，0．005，0．025；第三种，对于p1＝0．10，考虑Δ＝－0．05，－0．01，0，0．01，0．05，同时显著性水平定为95%，所有的模拟结果都是基于10，000次重复得到的，同时还考虑了x0＝x1＝15，在这种情形下p1和Δ的设置和上面的三种设定相同。模拟结果如图1、图2所示。

图1中左图表示覆盖概率（CP），右图表示期望区间宽度（ECW），显著性水平为95%，x0＝x1＝5；点虚线、用‘o’标记的实线、点线、虚线分别表示得分方法、GREUMVUE、似然比方法、GREMLE方法得到的结果。图2表示x0＝x1＝15的情形，其他与图1相同。

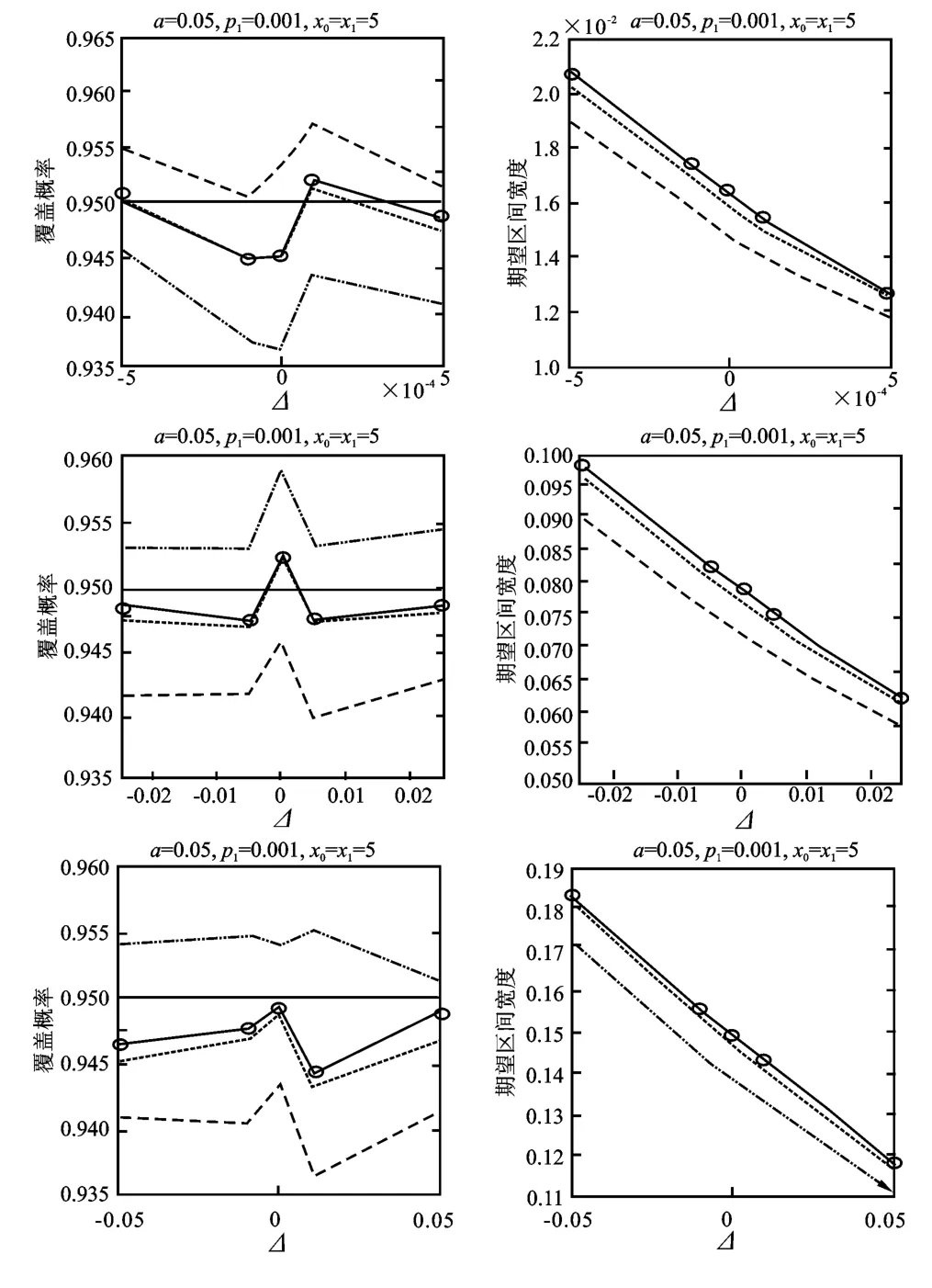
图1 覆盖概率（左）和期望区间宽度（右）模拟结果图

对于覆盖概率（CP），从图1可以清楚看出，与x0＝x1＝15相比，对于较小情形的x0＝x1＝5，得分方法构建的置信区间的覆盖概率一般比预先设定的置信水平大；对于较小的x0＝x1＝5，GREMLE置信区间的覆盖概率一般比预先设定的置信水平要小。需要指出的是，似然比方法以及GREUMVUE方法得到的置信区间可以较好地控制覆盖概率 。换言之，这两种方法得到的置信区间的覆盖概率都非常接近预先设定的显著性水平95%。比较似然比方法和GREUMVUE方法，从图1可以看出后者的覆盖概率更加接近设定的显著性水平。当将x0＝x1的值从5增加到15时，所有置信区间的覆盖概率都变得离置信水平很近，但从图2可以发现，在覆盖概率方面，本文所提出的GREUMVUE要表现得更好。

对于期望区间宽度（ECW），从图1和图2可以看出，当增加p1、降低Δ或者x＝x0＝x1的值时，估计的期望区间宽度（ECW）一般也会增加。同时也可以发现，得分方法所得到的置信区间的期望区间宽度（ECW）最短。

四、实际数据分析

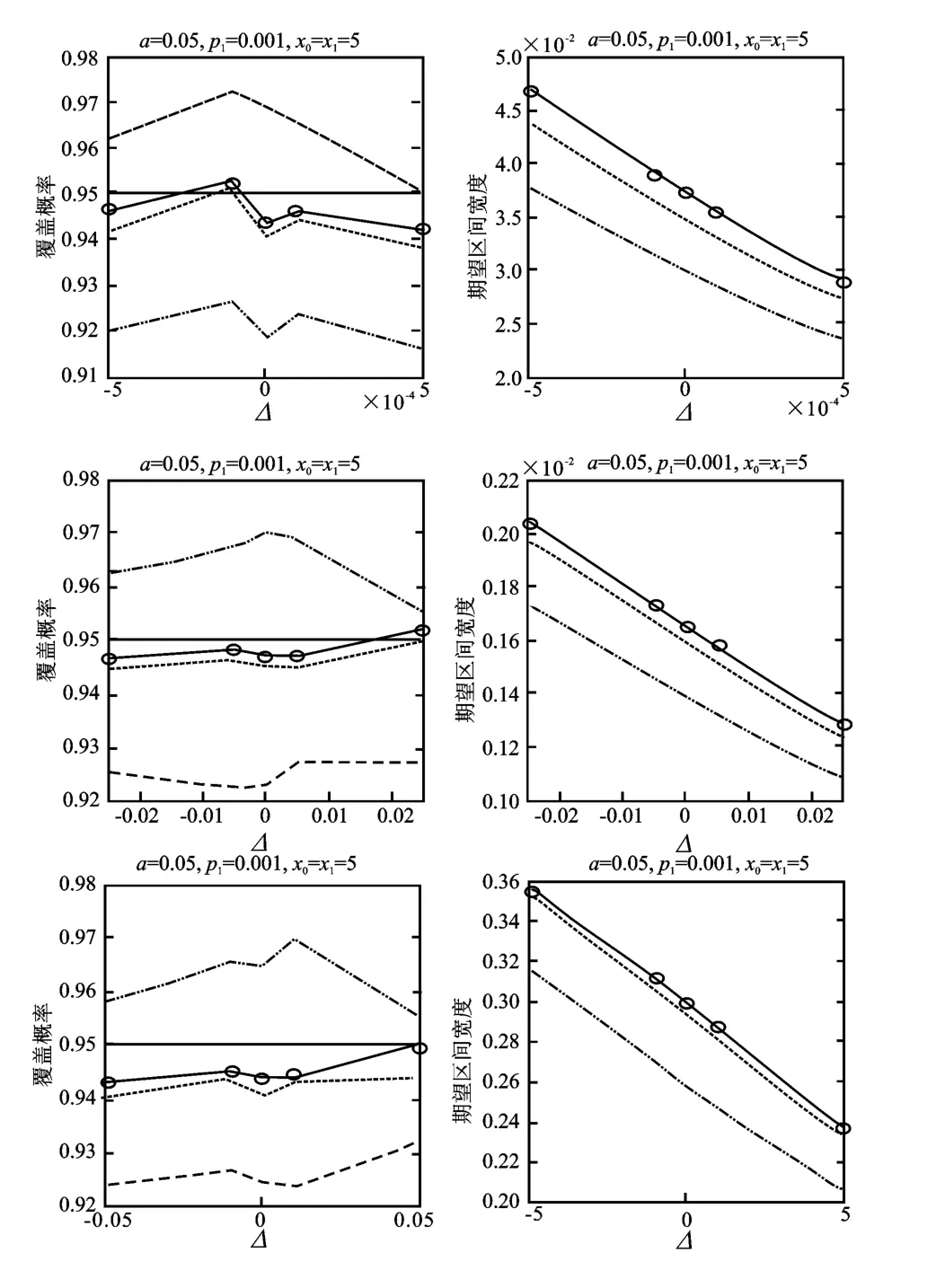
图2 覆盖概率（左）和期望区间宽度（右）模拟结果图

笔者分析Tang等人分析过的药物比较研究的实际数据，研究目的是探讨由两种药物导致的肝损伤的风险是否相同。实际数据来源于Hirji的《离散型数据的分析》一书，因为肝损伤是较为稀少的、急性的，严重时甚至是致命的一种疾病，所以在本研究中采用了逆抽样的抽样方式［14］67－68。因此，将来医院就诊的病人被随机分为两组，第一组病人服用药物0，第二组病人服用药物1，然后对这些病人进行随访，直到在两组中各得到x0＝x1＝5个患肝损伤的病人，最终在各组获得第5个肝损伤的病人之前，对于药物0，有y0＝53个没有肝损伤的病人，而对于药物1，有y1＝312个病人没有肝损伤。

对于以上数据，笔者感兴趣的是上述两种药物导致肝损伤的风险是否相同。根据上述逆抽样过程，通过计算可以得到＝－0．070 4，该点估计很小，故无法据此判断肝损伤风险差Δ是否显著。考虑Δ的95% 置信区间，通过计算可以得到基于似然比、得分、GREMLE和GREUMVUE方法的置信 区 间 分 别 为 ［－0．161 3，－0．013 1］，［－0．141 0，－0．004 6］，［－0．171 3，－0．018 4］，［－0．163 4，－0．013 5］。很明确，这4种方法可以得到同样的结论，亦即服用这两种药物导致肝损伤的风险的确是存在差异的。

五、结论与意义

本文的研究具有重要的理论意义。近年来，关于逆抽样过程的风险差和风险比的研究受到了国内外学者的广泛关注，很多学者采用Wald方法、得分统计量方法、似然比方法等各种各样的方法，对风险差和风险比进行了统计推断，诸如构造其置信区间，或是假设检验，或是确定试验设计中所需的样本量等。在此，笔者提出了两种新的基于梯度统计量构建逆抽样下风险差的置信区间的方法，分别基于风险差的极大似然估计（MLE）和方差最小无偏估计（UMVUE）方法，通过上述模拟分析可以知道笔者提出的方法都有令人满意的模拟表现。与现有的WALD方法、UMVUE方法和似然比方法更优之处在于，基于梯度统计量的方法既不需计算Fisher信息阵，也不需要计算其逆矩阵，这样计算量就得以大大简化，在计算上更加简便可行，从而避免了Wald统计量和得分统计量等传统的统计量计算复杂的弊端，具有重要的理论意义。

本文的研究还具有重要的实践意义。随机对照临床试验在临床流行病学、药学研究中应用广泛，基本上已经成为了任何新药研发的一个必经阶段。临床试验的重要性对于现代医学的发展不言而喻，通过临床试验可以得到很多重要的指标，风险差和风险比就是其中很重要的研究新旧差异的指标。因此，对于逆抽样过程的风险差和风险比的研究具有重要的实践意义，加之梯度统计量计算较传统的方法更加简便可行，这就为实践应用提供了更大的便利。

［1］ Haldane J B S．On a Method of Estimating Frequencies［J］．Biometrika，1945（3）．

［2］ Lui K J．Notes on Confidence Limits for the Odds Ratio in Case－control Studies Under Inverse Sampling［J］．Biometrical J，1996（2）．

［3］ Lui K J．Conditional Maximum Likelihood Estimate and Exact Test of the Common Relative Difference in Combination of 2Tables Under Inverse Sampling［J］．Biometrical J，1997（2）．

［4］ Tian M Z，Tang M L，Ng H K T，et al．Confidence Intervals for the Risk Ratio Under Inverse Sampling［J］．Stat．Med．，2008（17）．

［5］ Tang M L，Liao Y J，Ng H K T．On Tests of Rate Ratio Under Standard Inverse Sampling［J］．Comput．Meth．Prog．Bio．，2008（3）．

［6］ Tang M L，Tian M Z．Asymptotic Confidence Interval Construction for Risk Difference Under Inverse Sampling［J］．Comput．Stat．Data An．，2009（3）．

［7］ 戴明峰，金勇进，孙婕．Polya后验方法在有限总体抽样估计中的模拟研究［J］．统计与信息论坛，2013（4）．

［8］ Terrell G R．The Gradient Statistic［J］．Comput Sci Stat，2002（3）．

［9］ Lemonte A J，Ferrari S L P．The Local Power of the Gradient Test［J］．Ann．I．Stat．Math．，2012a（2）．

［10］Lemonte A J，Ferrari S L P．A Note on the Local Power of the LR，Wald，Score and Gradient Tests［J］．Electron．J．Stat．，2012b（6）．

［11］Lemonte A J．Local Power Properties of Some Asymptotic Tests in Symmetric Linear Regression Models［J］．J．Stat．Plan．Infer．，2012（5）．

［12］Lui K J．Interval Estimation of Simple Difference Under Independent Negative Binomial Sampling［J］．Biometrical J．，1999（1）．

［13］Farrington C P，Manning G．Test Statistics and Sample Size Formulae for Comparative Binomial Trials With Null Hypothesis of Non－zero Risk Difference or Non－unit Relative Risk［J］．Stat．Med．，1990（12）．

［14］Hirji K F．Exact Analysis of Discrete Data［M］．New York：Chapman ＆ Hall／CRC，2006．