半参数纵向模型的惩罚二次推断函数估计

赵明涛，许晓丽

（安徽财经大学a．统计与应用数学学院；b．管理科学与工程学院，安徽 蚌埠233030）

一、引 言

纵向数据涉及到对同一组受试个体在不同时间点进行重复观测，这种数据广泛产生于医学、经济学、社会科学等领域［1］1－20。这种重复观测的数据结构便于研究个体随时间变化的效应，却使得对同一个体的观测趋于相关，也即存在个体内相关性。个体内相关是个体观测之间真实关系的反映，然而在研究中却是未知的，因此如何处理个体内相关是纵向数据分析不可回避的问题和难点。实际中，若研究的重点在于分析响应变量与协变量的总体效应，可建立边际模型。边际模型是一种常见的纵向数据分析模型，该模型将均值和方差分开来进行建模分析，一定条件下只要均值模型假定正确，无论方差模型假定是否正确，总能获得均值部分的相合估计。

广义估计方程（GEE）是一种常见的边际模型分析方法，该方法不需要假设个体观测的联合分布形式，仅需对模型的低阶矩（一阶矩和二阶矩）进行假设［2］。不仅如此，广义估计方程将个体内相关视为讨厌参数，在一定条件下即使工作相关矩阵假设错误，仍然能得到回归参数的相合的、渐近正态的估计。然而广义估计方程存在着一些缺点：效率不高、稳健性不够、难以用于模型检验等［3］49－68［4］。

二次推断函数（QIF）则有效地克服了广义估计方程的这些缺点［5］。在处理个体内相关性的问题上，二次推断函数对工作相关矩阵的逆矩阵进行基矩阵展开近似，构造得分向量。然后，利用广义矩方法（GMM）构造自适应的目标函数，即为二次推断函数，最小化目标函数，便能得到二次推断函数估计［6］。形式上看，二次推断函数不含有讨厌参数，大大减小了估计复杂度，提高了估计的效率。理论结果显示，在一定条件下所得到二次推断函数估计总是相合的、渐近正态的和有效的。当工作相关矩阵假定正确时，二次推断函数估计和广义估计方程估计有同样低的渐近方差；当工作相关矩阵被错误假定时，在估计方程所有的线性组合中，二次推断函数估计量仍然是最优的，而拥有同样工作相关矩阵所得到的广义估计方程估计量则不是。不仅如此，从形式上看二次推断函数类似于二次得分统计量，因此可以被广泛用于模型检验问题，这个优点是广义估计方程所不具备的。

半参数边际模型是纵向数据分析中一类重要的模型，在模型拟合和降维问题方面都有着广泛的应用［7］。对于变系数模型，Qu和Li利用截断幂函数基对模型中的变系数进行基函数展开，构造关于基函数系数的二次推断函数［8］。为了避免出现过拟合问题，他们给所构造的二次推断函数添加一个惩罚项，从而得到关于基函数系数的惩罚二次推断函数。一定条件下，运用该方法可以得到关于基函数系数的相合的、渐近正态的、有效的惩罚二次推断函数估计量。然而，运用该方法却未能对变系数估计的渐近性质进行探讨，估计结果仅限于对变系数的非参数拟合。

随后，Bai和Zhu等则利用二次推断函数研究了纵向数据部分线性回归模型［9］。他们首先假设模型未知参数已知，然后采用B样条基展开近似模型中的非参数部分，进而构造关于参数部分的二次推断函数。通过理论证明，该方法仍然能得到参数部分的相合的、渐近正态的二次推断函数估计。该方法研究重点在于模型中参数部分的估计，而未对非参数部分做出深入的研究和探讨。随后Bai和Fung等则利用二次推断函数方法研究纵向数据单指标模型，他们利用截断幂函数基对未知联系函数进行展开近似，然后构造关于基函数系数以及单指标参数的惩罚二次推断函数，理论证明所得到的估计具有相合性和渐近正态性［10］。Lai等则提出了偏差修正QIF方法用以估计部分线性单指标模型，不仅得到了较好的渐近结果，还建立了广义似然比检验统计量用以检验非参数部分的线性关系［11］。

上述诸多成果研究的重点都在于模型中参数部分的估计性质的探讨，而未能涉及到非参数部分的估计性质。本文则结合惩罚样条和二次推断函数思想，构造关于参数部分和非参数部分的惩罚二次推断函数（PQIF），用以同时估计模型中的参数和非参数部分。

由于二次推断函数独特的函数结构，实际中我们并不能得到参数估计的显式解，只能利用数值方法得到数值解。诸多学者在处理这个问题时都选用了Newton－Raphson迭代算法。然而，该算法会涉及到矩阵求逆运算，实际中往往会遇到协方差矩阵难于估计，或者出现协方差矩阵奇异或近似奇异的情况，这会使得一般的迭代算法不能实现或者计算量太大，从而得不到满足条件的二次推断函数估计。针对这些问题，部分学者从以下三方面对二次推断函数估计的求解做了深入的研究：（1）修正和改造扩展得分方程的协方差矩阵结构；（2）修正数值迭代方法，避免矩阵求逆运算；（3）针对实际问题或提出新的迭代算法。

Qu和Lindsay等则提出了一种不需要对作业相关矩阵进行假设的自适应的估计方程方法［12］。他们利用共轭梯度法在多变量情况下的推广，找到在一些固定的低维上保留信息良好的估计方程，以找到一个较好的协方差矩阵的逆矩阵的近似，这种方法对于协方差阵奇异、近似奇异或者由于数据量太大而难以求解的情况非常有效。

在固定设计情形下，Han等利用一个最优权矩阵的一个线性收缩估计量代替样本协方差阵。所构造的线性收缩估计量总是可逆的，而且在大样本情况下是相合的、渐近最优的，同时在期望二次损失意义下要比样本协方差阵更加稳定，使得迭代算法总能实现［13］。Loader等提出了关于代重复加权最小二次算法，该算法要比Newton－Raphson算法更加稳定，更加有效［14］。

Khan等则指出了Newton－Raphson算法本身的一些缺点，比如奇异的雅克比矩阵可能会导致算法无法进行，矩阵求逆运算会使得算法本身的运算量太大［15］。为了克服这些缺点，他们利用割线法进行迭代求解，而且对比研究了割线法和Newton－Raphson算法在有限样本情况下的表现，结果显示割线法更优。鉴于此，本文利用割线法迭代求解。

本文介绍了惩罚二次推断函数估计方法，建立了估计的大样本性质，探讨了估计方法中一些参数的选取问题，最后给出模拟结果和结论。

二、模型估计方法

不妨假设纵向数据集 ｛（xij，tij，yij）：i＝ 1，2，…，N；j＝1，2，…，ni｝，满足：

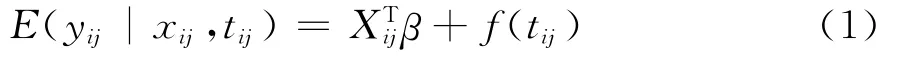
其中tij、yij及xij分别为第i个个体的第j次观测时刻点及相对应的响应变量和协变量，β为p×1维回归参数，f（t）为未知光滑函数。假设：

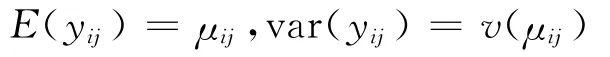
其中v（·）为已知方差函数。采用截断幂函数基对f（t）进行基函数展开近似，具有K个节点的k阶截断幂函数基为：

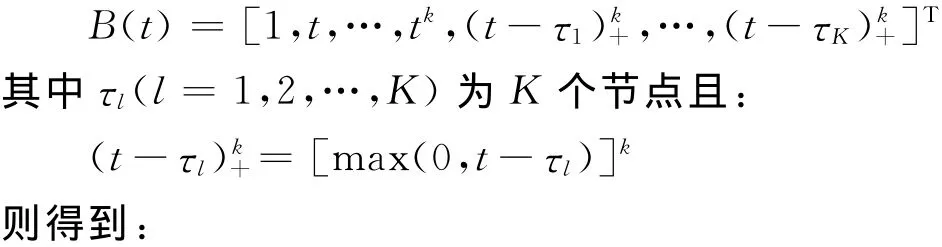
Step 1：给定迭代初始值（0）、（1）及充分小的阀值ε；

Step 2：根据式（7）迭代求解（j）和（j＋1）；

Step 3：判断：若｜｜（j＋1）－（j）｜｜＜ε，则终止计算，此时＝（j＋1）即为θ的惩罚二次推断函数估计。否则，返回Step 2继续迭代运算。

三、估计的大样本性质

大样本性质是估计方法的理论基础。统计研究中，估计结果和真实结果之间往往会存在一些偏差，这些偏差主要由两方面因素引起：样本的随机性和有限性以及估计方法自身的缺陷。实际中由样本因素所造成的偏差往往无法避免，但可以选择合适的估计方法以降低估计偏差。如何评价估计方法的优劣呢？常见的手段就是探讨估计结果在大样本情况下的极限性质，即为大样本性质。如果大样本情况下，估计的渐近结果和真实结果一致，则有理由相信估计方法比较好，反之则较差。常见的渐近结果包括渐近无偏性、一致性和渐近有效性等。为了建立估计的大样本性质，首先给出如下一些必要的假设条件。

上述假设条件是本文估计方法大样本性质的前提条件。首先C1可以保证二次推断函数在大样本情况下有意义；C2是模型的识别条件，使得理论上的估计结果存在且唯一；C3是参数空间的紧性和内部性假设条件，紧性和内部性的假设不仅使得估计结果是参数空间的全局最优解，而且使得GMM的一阶条件成立；C4和C5是在证明大样本性质时的一些必要的数学假设条件，在证明估计结果的大样本性质时起着重要作用。下面给出估计的大样本性质，主要包括估计的相合性、渐近正态性及渐近有效性。

定理1：假设条件（C1至C4）均满足，且λ＝o（1），则通过式（6）得到的存在且以概率收敛到θ0。

证明：由惩罚二次推断函数的非负性、连续性和有界性可知一定存在。任取θ0一个邻域U，假设U的补集为Uc，则U为开集且Uc为闭集。不妨定义｜Ω0－1／2E（gi（θ））｜2为Ω0－1／2E（gi（θ））的内积，由条件

四、实际应用

实际运用中，需要选择截断幂函数基B（t）和调整参数λ。B（t）的选择包括阶数k和节点τ的选择。为了避免过拟合问题，往往选择阶数较低的B（t），节点的选择则包括节点个数及位置的选择。节点个数不宜过多，往往在5～10个之间，节点位置往往可以选用等分位点或者等距点［16］。

调整参数λ的大小控制着模型拟合程度，是一个非常重要的参数。实际中，往往利用广义交叉验证方法选择合适的值。定义一个广义交叉验证统计量［8］：

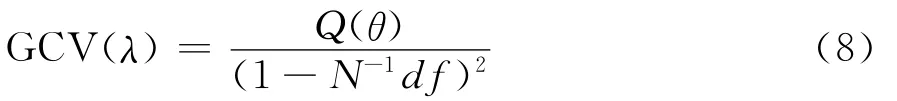
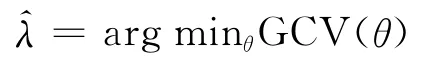
实际应用中，利用格点搜索的办法来选择合适的λ值。

五、数值模拟

利用数值方法来考察上述模型估计方法在有限样本情况下的表现。考虑模型：

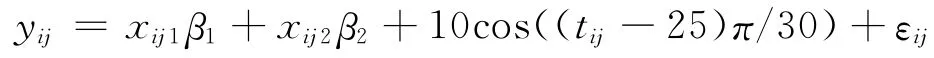
模型中真实的回归参数β1＝2，β2＝6，xij1＝tij＋δij，δij～N（0，1），xij2服从成功概率为0．5的伯努利分布，εij～N（0，2），观测个体数目N＝200，个体被观测的时刻点集为｛0，1，2，…，30｝，真实的观测时刻点与规定的观测时刻点之间的误差服从均匀分布U（－0．5，0．5），除了零时刻外，其它每个时刻点缺失的概率为0．6。假设个体内的相关结构为可交换结构且ρ＝0．8。选用具有5个节点的三阶截断幂函数基，节点位置为时间点的5等分位数点。利用式（6）求θ的惩罚二次推断函数估计。模拟次数为200次，估计结果记为（l＝1，2，…，200），分别计算：得到结果如表1。重新生成一组数据，得到未知平滑函数的拟合结果如图1。

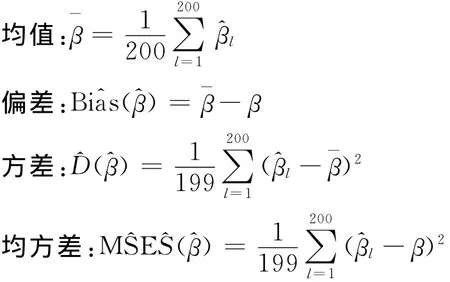
表1 回归参数β的估计结果表

表1给出了利用本文估计方法所得出的关于回归参数β的估计结果及其精度，包括样本均值、偏差、方差和均方差。图1给出了模型中的未知平滑函数的估计曲线和真实曲线的对比图像，其中实线为真实曲线，虚线为拟合曲线。

从表1可以看出本文所提出的惩罚二次推断函数估计方法对于半参数模型中的参数部分的估计效果很好，精度很高。从图1看到，图中虚线（真实曲线）和实线（拟合曲线）几乎重合，这说明估计方法对模型中的非参数部分的估计效果也很好。

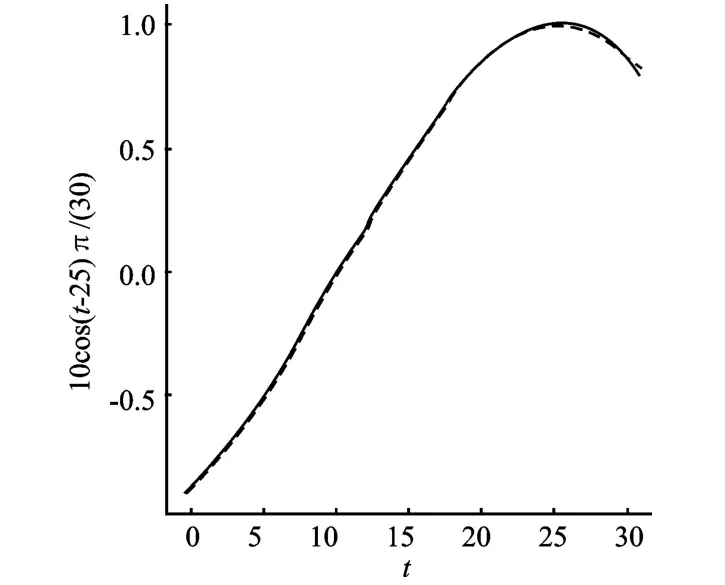
图1 f（t）的估计结果图

六、结 论

探索变量之间的关系一直是统计研究领域的重点问题，回归分析方法则是解决此类问题的一个有效的统计分析方法。近年来，随着计算机技术的飞速发展，越来越多的半参数回归模型被提出来用以探求自变量和因变量之间的复杂关系。半参数模型兼有参数模型和非参数模型的优点，在数据降维问题上有着广泛的应用。实际中，由于研究领域的不同，利用半参数模型处理的数据类型可能会更加复杂。相关性数据主要是指重复测量数据，包括经济领域的面板数据以及医学领域的纵向数据。个体内相关性的处理是分析这类数据的难点，二次推断函数方法则可以巧妙地解决这个问题。

本文提出的方法重在对参数部分和非参数部分同时进行估计，方法本身简单易懂，同时还可以探讨非参数部分的一些估计性质，弥补了诸多研究结果的不足，具有很强的理论价值和应用价值。不仅如此，本文提出的方法具有很强的推广性，可以用于估计重复测量数据情形下的部分线性变系数模型、部分线性单指标模型、部分线性可加模型等。其主要技巧仍然是通过选择合适的基函数对模型中的非参数部分进行展开近似，将非参数部分的估计参数化，进而建立惩罚二次推断函数。可以证明的是，这类估计方法具有较好的大样本性质，可以得到很好的推广运用。

［1］ Diggle P，Heagerty P，Liang K－Y，et al．Analysis of Longitudinal Data［M］．New York：Oxford University Press，2002．

［2］ Liang K－Y，Zeger，S L．Longitudinal Data Analysis Using Generalized Linear Models［J］．Biometrika，1986，73（1）．

［3］ Fan J，Lin X．New Developments in Biostatistics and Bioinformatics［M］．New York：World Scientific，2009．

［4］ Crowder M．On the Use of a Working Correlation Matrix in Using Generalised Linear Models for Repeated Measures［J］．Biometrika，1995，82（2）．

［5］ Qu A，Lindsay B G，Li B．Improving Generalised Estimating Equations Using Quadratic Inference Functions［J］．Biometrika，2000，87（4）．

［6］ Hansen L P．Large Sample Properties of Generalized Method of Moments Estimators［J］．Econometrica，1982，50（4）．

［7］ 张波，方国斌．高维面板数据降维与变量选择方法研究［J］．统计与信息论坛，2012，27（6）．

［8］ Qu A，Li R．Quadratic Inference Functions for Varying－Coefficient Models with Longitudinal Data［J］．Biometrics，2006，62（2）．

［9］ Bai Y，Zhu Z，Fung W K．Partial Linear Models for Longitudinal Data Based on Quadratic Inference Functions［J］．Scandinavian Journal of Statistics，2008，35（1）．

［10］Bai Y，Fung W K，Zhu Z Y．Penalized Quadratic Inference Functions for Single－index Models with Longitudinal Data［J］．Journal of Multivariate Analysis，2009，100（1）．

［11］Lai P，Li G，Lian H．Quadratic Inference Functions for Partially Linear Single－index Models with Longitudinal data［J］．Journal of Multivariate Analysis，2013，118（1）．

［12］Qu A，Lindsay B G．Building Adaptive Estimating Equations When Inverse of Covariance Estimation is Difficult［J］．Journal of the Royal Statistical Society：Series B（Statistical Methodology），2003，65（1）．

［13］Han P，Song P X K．A Note on Improving Quadratic Inference Functions Using a Linear Shrinkage Approach［J］．Statistics ＆Probability Letters，2011，81（3）．

［14］Loader C，Pilla R S．Iteratively Reweighted Generalized Least Squares for Estimation and Testing with Correlated Data：An Inference Function Framework［J］．Journal of Computational ＆ Graphical Statistics，2007，16（4）．

［15］Khan N M，Heenaye M．A Computationally Efficient Algorithm to Solve Generalized Method of Moments Estimating Equations Based on Secant－Vector Divisions Procedure［J］．International Journal of Scientific and Statitical Computing，2011，2（1）．

［16］Ruppert D．Selecting the Number of Knots for Penalized Splines［J］．Journal of Computational and Graphical Statistics，2002，11（4）．