奇异振荡现象与多模振荡现象以及一类新型振荡器的研究*
2013-12-30于红兵陈启兴张金华
于红兵,陈启兴,张金华
(成都信息工程学院通信工程系,成都610225)
文献[1-2]对反馈型正弦波振荡器的起振条件提出了一种新见解。由于起振问题是线性电路在零激励条件下的本征问题,因而应采用线性微分方程的理论方式处理起振过程,得到普适的电路起振判据:存在复数s0,使复频域中的环路增益T(s0)=1,Re(s0)>0,且lm(s0)≠0。(s0正是微分方程通解所涉及的特征根,而T(s0)=1是特征方程,以上条件说明特征根在右半平面。)并指出在接近平衡态时,电路起振的充分必要条件可以表达为相量形式,即以下(A)(B)两组条件之一得到满足:

式中φT(ω)是T(jω)的幅角。文献[2]根据普适的电路起振判据,详细讨论了文氏电桥振荡器及变压器耦合振荡器中满足起振条件的元件参数范围,证实了这种复频域分析法对于判断电路能否起振具有很好的全域预测能力。文献[1]指出,用相量法分析,现有的常规振荡器能够满足T(jω1)>1,且∂φT(ω)/∂ω|ω=ω1<0,这两条合在一起,才使电路可以起振。相量法的恰当应用与新电路设计的范例见文献[3]。
本文将在以上工作的基础上,探讨电路起振时相量形式环路增益的可能变化形式,并辨析由此导致的电路不同终态。与此相伴的,是对振荡现象和振荡器工作机制的完整细分,和对相量法分析工具的适用性及其简便而合理的应用方式的新认识。
1 近平衡态起振的延拓与振荡现象
以T(jω1)略大于1的近平衡态起振时,特征根在右半平面内接近于虚轴。如果改变元件参数使T(jω1)逐渐变得更大,特征根将渐渐远离虚轴。当特征根最后落在右半实轴时,电路不再能够起振。对于T(jω1)小于1的情况也有类似分析。所以对于每个具体电路,能够起振的T(jω1)取值范围(可以称为“有效起振区间”)有可能是从1(不包括1)向右延拓至某个大于1的实数(不包括这个数本身);也有可能是从1(不包括1)向左延拓至某个小于1的实数(不包括这个数本身)。
以式(1)中的(B)组条件实现近平衡态起振时,至少是实现了T(jω1)<1的起振。在这种情况下,它还有进一步向左延拓至负数的可能,从而实现T(jω1)为负值的起振!
总的来说,根据式(1)的(A)或(B)两组相量形式的起振条件,可以确知“有效起振区间”的下限或上限为“1”。
电路最终能否实现平衡振荡,则是另外一个问题。平 衡 条 件 为T(jω1)=1[4-6],只 是 式 中的T(jω1)是当信号X(t)逐渐增大后因元件参数改变而得到的相应值。
电路起振时如果满足
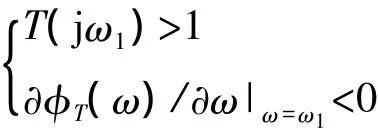
为了最终满足平衡条件T(jω1)=1,则要求∂T/∂X<0。具有∂T/∂X<0这种特性的电路是常见的(只需内稳幅即可)[4-6],所以这种特性可以称为常规的非线性特性。
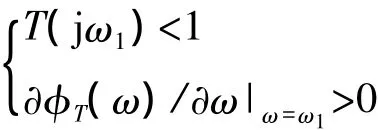
为了最终满足T(jω1)=1,则要求∂T/∂X>0。但是,具有∂T/∂X>0这种特性的电路是不常见的,所以这种特性可以称为非常规的非线性特性。当以的非线性特性时,电路不能自动实现平衡振荡。其中发生的信号过程应当是:先产生增幅振荡,当信号达到一定强度后,振荡信号反而消失。这种信号过程不同于不能起振的电路中在电路接通后由于电流冲击而产生的减幅振荡信号衰减过程。这种具有新机制的信号现象可称为奇异振荡现象,相应的电路称为奇异振荡电路。
2 不同类型电路的起振条件分析
以下各电路均为最简形式的交流通路,以突出本质内容。在每种情况下所列举的电路个数以能够说明问题为限(T(jω1)大于1的起振是为了对比讨论而写下的)。以下每种情况都有更多的电路实例没有例举。本文中这些电路设计出来,主要目的在于有对比性地、系统性地对理论分析的各种可能性加以验证,但这并不妨碍其可能的实用价值。
2.1 T(jω1)大于1的起振
考虑图1所示电路。

复频域的环路增益
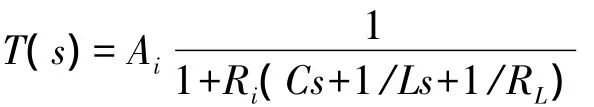
起振条件为


图1 T(jω1)大于1起振的电路
相量形式的环路增益为

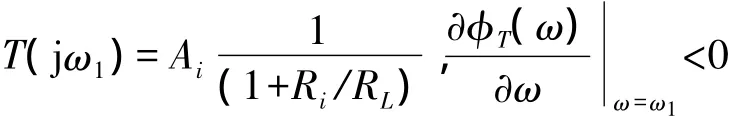
只要Ai比1+Ri/RL略大一些,就能满足近平衡态起振的(A)组要求,从而使电路起振。T(jω1)的“有效
2.2 T(jω1)小于1的起振
2.2.1T(jω1)小于1而起振的电路例1考虑图2所示电路。复频域的环路增益为
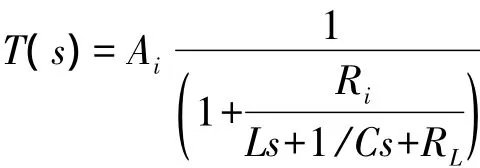
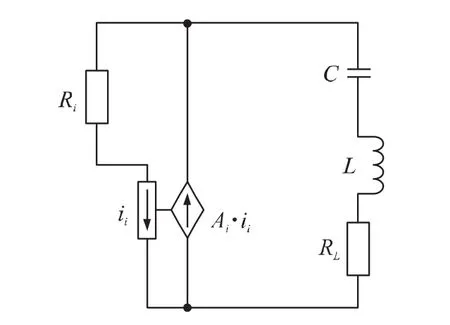
图2 T(jω1)小于1起振的电路之例1
起振条件为
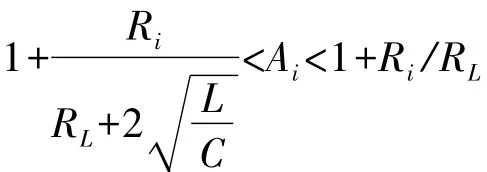
相量形式的环路增益为
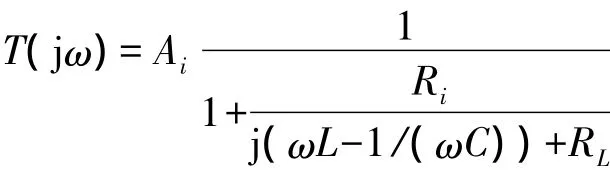
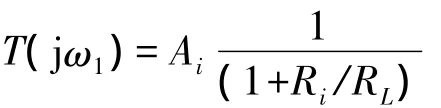

以上过程通过递进推算确定T(j(ω1+Δω))所在的象限,以此确定了符号,这种方法可以称为判断符号的象限法,又可称为平衡态偏离法(即考查由于频率的偏离Δω所导致的T(jω)的偏离情况)。
只要Ai比1+Ri/RL略小一些,就能满足近平衡态起振的(B)组要求,从而使电路起振。T(jω1)的“有效起振区间”是
2.2.2T(jω1)小于1而起振的电路例2
考虑图3所示电路。复频域的环路增益为
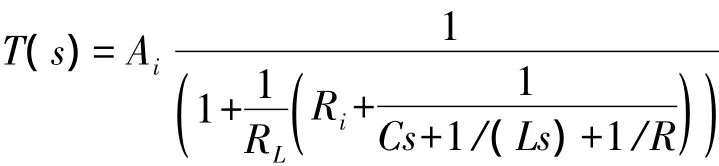
起振条件为


图3 T(jω1)小于1起振的电路之例2
相量形式的环路增益为
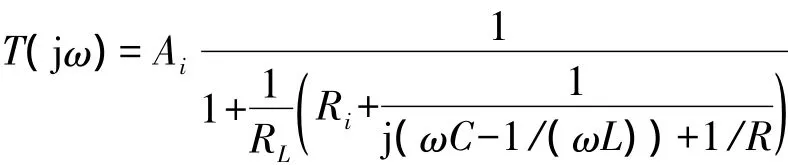
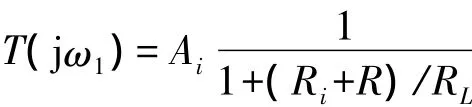
2.2.3T(jω1)小于1而起振的电路例3
考虑图4所示电路。复频域的环路增益为起振条件为


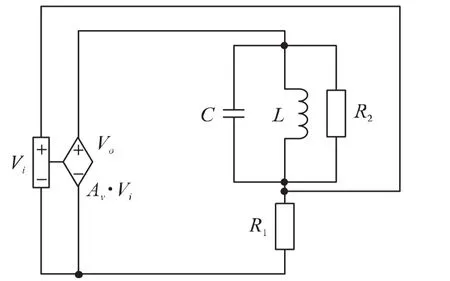
图4 T(jω1)小于1起振的电路之例3
相量形式的环路增益为

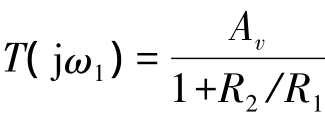
2.3 可以将T(jω1)延拓为负数的起振
2.3.1 可以将T(jω1)延拓为负数的起振例1
考虑图5所示电路。复频域的环路增益为
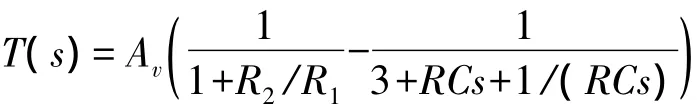
起振条件为
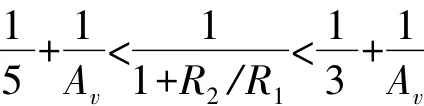

图5 可以将T(jω1)延拓为负的起振电路之例1
相量形式的环路增益为
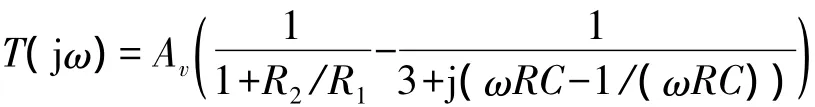
T(jω1)的“有效起振区间”是。具体说来,当Av的值大于而小于时,满足起振要求的R2/R1都是小于2的,电路只能以T(jω1)小于1的正数而起振;当Av的值大于时,通过改变T(jω1)可以为正或为负。其细分情况如下:满足时,电路仍是以T(jω)小于1的1正数而起振的;但时,电路是以T(jω1)为负数的情况而起振的。这时实现的是负反馈条件下的起振。
2.3.2 可以将T(jω1)延拓为负数的起振例2
考虑图6所示电路。复频域的环路增益为
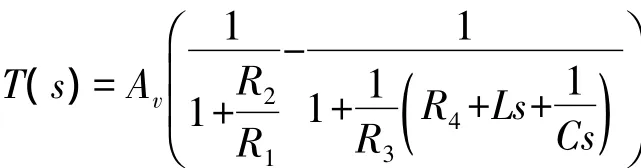
起振条件为
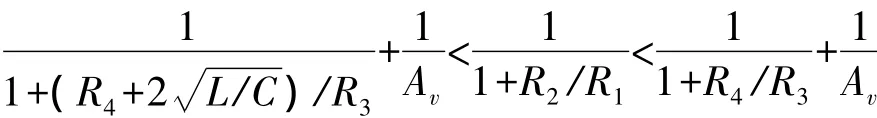

图6 可以将T(jω1)延拓为负的起振电路之例2
相量形式的环路增益为

v只是比稍小一点,保证T(jω1)>0,这时应用象限法,可知0。因而满足近平衡态起振的(B)组要求,使电路起振。但还需考虑的是,根据复频域分析的结果,再虑及,因此要求1, 所 以Av的 取 值 必 须 大 于时才有可能起振。
T(jω1)的 “有 效 起 振 区 间 ” 是。具体说来,如果Av的值大于而小于,满足起振要求的R2/R1都是小于R4/R3的,电路只能以T(jω1)小于1的正数而起振;如果Av的值大于,通过改变可以为正或为负。其细分情况如下:满足时,电路仍是以T(jω1)小于 1的正数而起振的;但时,电路是以T(jω1)为负数的情况而起振的。
3 实验内容总结
为了全面地实现以上各个电路中可能获得的信号现象,并取得较大的元件参数变化范围,同时也为了排除次生现象的无谓干扰,对定量关系做出精确的验证,可以用仿真软件Multisim中的理想元件直接接成近乎理想的电路进行仿真实验。由于这样接出的电路中不含直流源,为获得引入微小的扰动,可以在电路中接入适当的噪声源或微小的单脉冲源。大量的仿真实验现象、数据及其解释归纳如下:
(1)起振条件的相对误差在104量级。由于理想线性元件不存在非线性效应,起振后信号将无限增加,只会在仿真过程的数值超出运算数值的极限时终止。
与文献[2]中的讨论类似,远离平衡态起振时信号振幅增长很快。这是由于相应特征根的实部较大而虚部较小所导致的,但在这种情况下起振时信号从微小扰动开始变大的模式仍为增幅振荡形式,表现为双向波动,而与实指数增长的单向增长不同。
(2)可以通过将图7所示的等效非线性电阻并联接入电路中的不同位置,使整个电路具备∂T/∂X<0或∂T/∂X>0的非线性特性,从而获得信号过程的不同终态。具体情况是:对图1所示电路,如果等效非线性电阻并联在RL上,通过调整RA的值,信号的终态可以达到平衡振荡。原因在于,起振后随着信号的增加,并联了非线性电阻的等效RL减小,T(jω1)由起振时的大于1最终减小到1。如果等效非线性电阻并联在Ri上,并排除其他器件的非线性特性的影响,信号将成为奇异振荡(见图8)。原因在于,起振后随着信号的增加,并联了非线性电阻的等效Ri减小,T(jω1)由起振时的大于1继续增加,无法实现平衡条件T(jω1)=1。
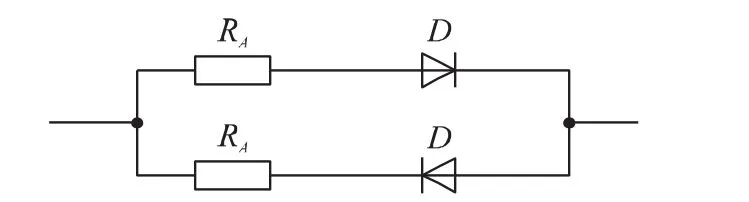
图7 等效为非线性电阻的结构
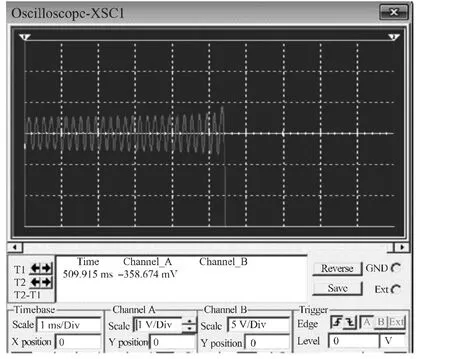
图8 奇异振荡现象
对图2所示电路,如果等效非线性电阻并联在Ri上,通过调整RA的值,信号的终态可以达到平衡振荡。原因在于,起振后随着信号的增加,并联了非线性电阻的等效Ri减小,T(jω1)由起振时的小于1最终增加到1。如果等效非线性电阻并联在RL上,信号将成为奇异振荡。原因在于,起振后随着信号的增加,并联了非线性电阻的等效RL减小,T(jω1)由起振时的小于1继续减小,信号的终态无法实现平衡振荡。
对图3所示电路,如果等效非线性电阻并联在Ri或R上,信号的终态可以达到平衡振荡。如果等效非线性电阻并联在RL上,信号过程成为奇异振荡。
对图4所示电路,如果等效非线性电阻并联在R2上,信号的终态可以达到平衡振荡。如果等效非线性电阻并联在R1上,信号过程成为奇异振荡。
对图5所示电路,如果等效非线性电阻并联在R2上,信号的终态可以达到平衡振荡。如果等效非线性电阻并联在R1上,信号过程成为奇异振荡。
对图6所示电路,如果等效非线性电阻并联在R2或R3上,信号的终态可以达到平衡振荡。如果等效非线性电阻并联在R1或R4上,信号过程成为奇异振荡。
(3)对于图2或图6所示电路,如果将电路调整为近平衡态起振,同时将电路中的LC串联回路替换为图9所示的LC串并联结构,则电路起振时将存在双模振荡现象(见图10),而终态的现象与替换前相同。这是因为电路中在处满足,按文献[1]的方法来讨论,在复平面上jω1的右边邻近处存在特征根s01,电路中相应地存在信号模式es01t;在处同样也满足,在复平面上jω2的右边邻近处存在特征根s02,电路中相应地存在信号模式es02t。因而至少在近平衡态起振时存在双模振荡现象。类似地也可以获得更多信号模式的同时起振现象。
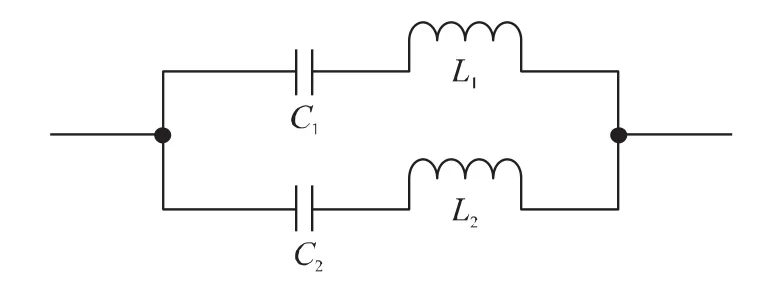
图9 LC串并联结构
即使电路中不含非线性电阻,一般来说各个模式的信号也存在着模式竞争的问题,这可以归咎于相应特征根的实部不同。如果时间足够长,将只有实部最大的特征根对应的模式可以观察到。但如果各支路的电感相同而电容不同,则各个模式都将一直维持其大小比例,从而保持了单模情况下特征根的实部与电容无关的特点。
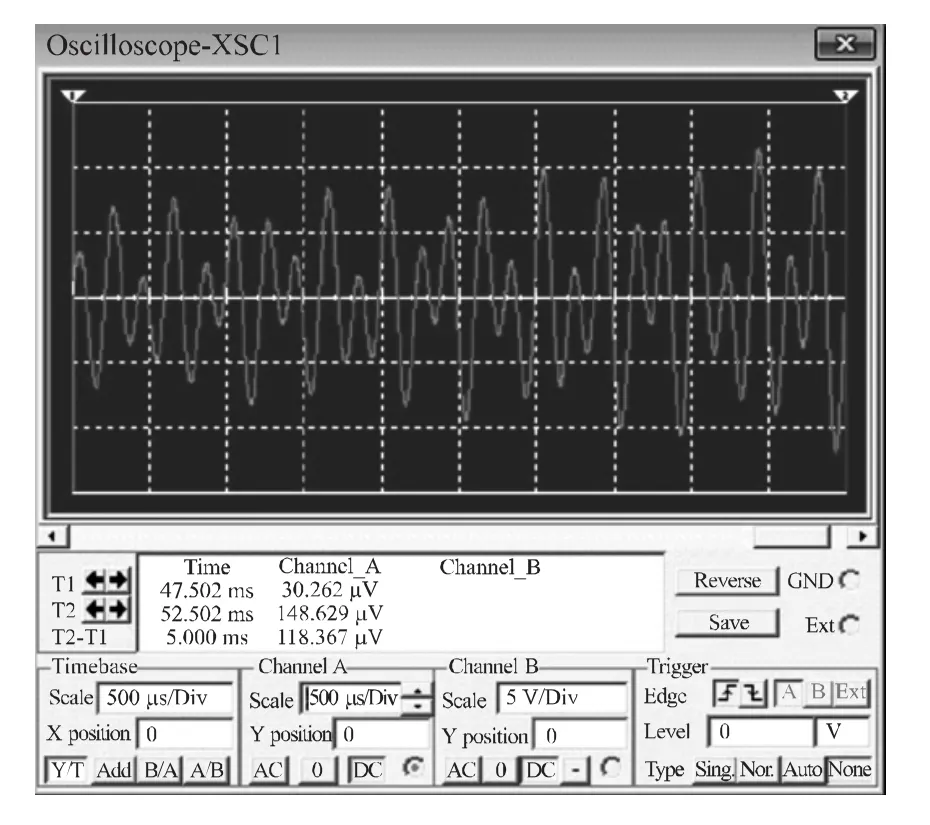
图10 起振时的多模振荡现象
(4)对图5和图6所示两个电路(振荡电路),每一个都可以转化为放大电路,而这个放大电路的增益与原振荡电路的环路增益相同。以图5所示电路为例,转化得到的放大电路如图11所示。如果将这个放大电路的输入端和输出端相连接,电路又会变回原来的图5所示振荡器。对于图5所示振荡器,约束关系为

所以图5所示振荡器环路增益为
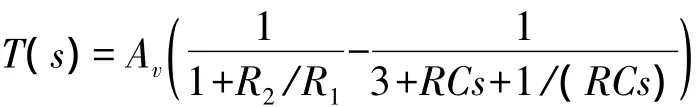
对于图11所示放大电路

所以图11所示放大电路增益为
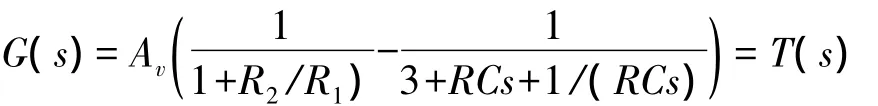
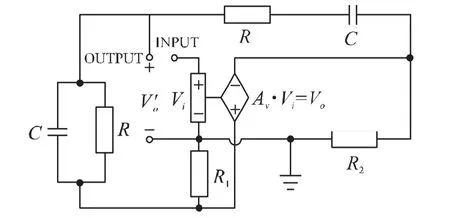
图11 由图5转化而来的放大电路
区别在于,对于振荡电路,如果T(s0)=1,则es0t模式的信号可以自主地存在于电路中;而在放大电路中,需要在输入端加上Aest形式的信号,使输出端得到信号G(s)Aest或T(s)Aest(即使在满足T(s0)=1的情况下也是如此)。当然,如果在输入端加上Aejωt形式的信号,输出端便得到信号G(jω)Aejωt或T(jω)Aejωt。也就是说,通过将振荡电路转化为放大电路,再输入一个正弦信号,测量其输出信号与输入信号的大小之比与相位差,由此得到放大电路相量形式的增益G(jω),从而得知对应的振荡电路环路增益T(jω)。可以就此验证在不同元件参数下振荡电路T(jω)的正负以及具体数值。特别有意义的是,对图5和图6所示两个电路,从理论分析得到的T(jω)的“有效起振区间”的上界和下界,都可以用这种方法进行实验验证。对于除“1”之外的另一个界线点,误差不超过2%(界线点“1”的误差在10-4)。
4 结论
用相量形式的分析讨论起振问题,本质上就是依据环路增益在虚轴上jω1处的取值特点来考察特征根的取值特点。作为一种简便的分析方式,其有效性与局限性在本文中都得到了详细阐述,使这种工程上常用但过去并未严格论证的分析方法获得了恰当的表达方式,并且提出了用于判断∂φT(ω)/∂ω|ω=ω1符号的象限法,进一步简化了运算。
实验结果证实了文献[1]的理论分析结论:T(jω1)>1既不是电路起振的充分条件,也不是电路起振的必要条件;T(jω1)>1或T(jω1)<1都能起振,但两种情况下都需要附加条件(即∂φT(ω)/∂ω|ω=ω1的符号)的配合。对于单个电路中的多模振荡情况(无论频率高低相差如何),仍然遵循这一原则。这些实验结果构成了对于传统振荡器理论[4-6]的证伪。
首次提出了电路的奇异振荡现象,并证实了它作为一大类振荡现象而普遍地存在。用相量法讨论,电路有两种获得奇异振荡现象的方式:通过具备∂φT(ω)/∂ω|ω=ω1>0,T<1(T的实际取值为小于 1 的正数或负数),∂T/∂X<0的特点而获得;或通过具备∂φT(ω)/∂ω|ω=ω1<0,T>1,∂T/∂X>0 的特点而获得。反之,电路最终获得稳定振荡信号的方式也有两种:通过具备∂φT(ω)/∂ω|ω=ω1<0,T>1,∂T/∂X<0 的特点而获得;或通过具备∂φT(ω)/∂ω|ω=ω1>0,T<1(T的实际取值为小于1的正数或负数),∂T/∂X>0的特点而获得。具备前一种特点的振荡器正是目前常见的振荡器;而具备后一种特点的振荡器实际上成为一类新型振荡器,称为非常规的振荡器。振荡现象的丰富性以及各类现象的存在方式的对称性不应该被视为某种出人意料的结果,而应被看成是严谨的理论工具对客观现象统一性的深入把握。这些丰富的内容决不能再用传统振荡器理论来分析和理解。
就起振条件的理论分析工具而言,有复频域分析方法和相量法形式下的分析,两者可以相互印证,说明理论是自洽的;多模振荡的存在,更显示了相量法形式分析的有效性和方便性;实验不仅验证了不同条件下振荡现象的波形的不同,也验证了起振条件所要求的元件取值的准确范围,还验证了关于相量形式环路增益取值的“有效起振区间”的存在。
作为文献[1-3]所开启的工作方向的深化,本文通过设计多个电路实例,从中挖掘出丰富的振荡现象,并发展出一系列新的概念和处理方法,基本上可以建立起关于振荡现象和振荡器的比较完整的阐释系统。本文的内容,不是对已有理论的修补,而是另起炉灶的新构造。
[1]于红兵.反馈型振荡器起振条件的新研究[J].电子科技大学学报,2005,34(4):573-576.
[2]于红兵,王天宝.反馈型正弦波振荡器起振的元件参数分析[J].四川师范大学学报(自然科学版),2005,28(6):744-746.
[3]于红兵,陈启兴.Y型接法的新型三点式振荡器的设计与研究[J].电子器件,2012,35(5):522-525.
[4]曾兴雯,刘乃安,陈健.通信电子线路[M].北京:科学出版社,2006.
[5]杨金法,彭虎.非线性电子线路[M].北京:电子工业出版社,2003.
[6]Muhammad H Rashid.Microelectronic Circuits:Analysis and Design[M].Cengage Learning,USA,2011.
