极板截面椭圆化对圆柱形电容器耐压能力的影响*
2013-12-30王福谦
王福谦
(长治学院电子信息与物理系,山西长治046011)
圆柱形电容器由于受力或工艺问题,可成为椭圆柱形电容,这一变化对电容器的电容量及耐压能力都将产生影响,使电容器的性能指标偏离设计值。有关文献[1-9]仅讨论了椭圆柱形电容器的电容量及电势和场强(标量式)分布,但对由于极板截面椭圆化对圆柱形电容器耐压能力影响的定量分析,相关文献还未见涉及.为此,笔者拟利用保角变换和数学软件研究此问题。
1 椭圆柱与圆柱横截面之间的变换
图1为一长、短半轴分别为a、b的长直椭圆柱导体的横截面.在复平面z上,以椭圆中心为原点建立坐标系,场点的位置为P(x,y)。经如下的儒可夫斯基变换

图1 导体椭圆柱的横截面及其外部的场点

式(1)中的c为椭圆的半焦距,如图2所示,w复平面上的圆w(u,v)=Reiθ就变换为图1中z平面的椭圆.图2中的导体截面圆的半径为R=(a+b)/c,而与z平面上的场点P(x,y)对应的w平面上场点P'(u,v)的位置坐标及其矢径r以下两式[10]确定
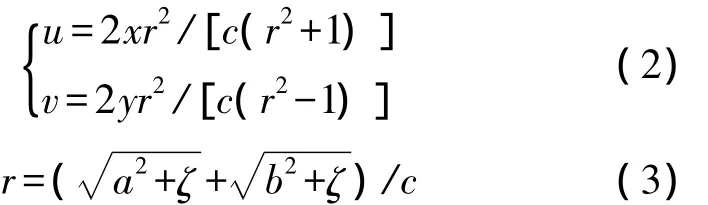
其中
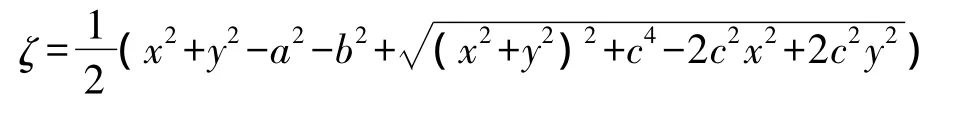
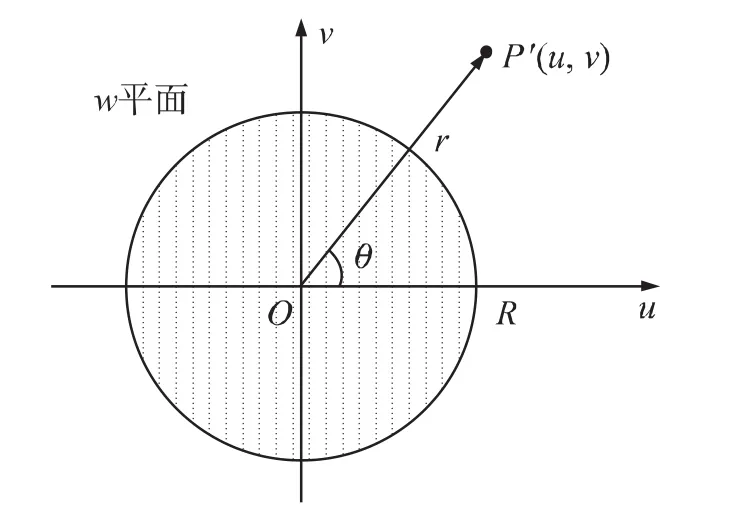
图2 变换后的导体圆柱及其外部的场点
2 椭圆柱与圆柱电容器横截面的变换
图3为一长、短半轴分别为a1、b1和的a2、b2长直共焦椭圆柱形电容器的横截面.内、外导体之间的电压为U0,其间为真空。在这个区域中,电势满足拉普拉斯方程。经变换式(1)后,w复平面上的两同心圆w(u,v)=R1eiθ和w(u,v)=R2eiθ(见图 4),变换为图3中z平面上的两共焦椭圆.图4中的两圆的半径分别为R1=(a1+b1)/c和R2=(a2+b2)/
由于在w平面上电容器的横截面的形状为圆形,即为圆柱形电容器,其内部电场在该截面上呈对称分布,故在w平面上可按圆柱形电容器的情形来讨论电场分布规律.
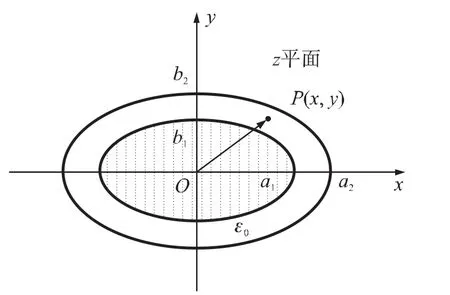
图3 椭圆柱形电容器的横截面及其内部的场点
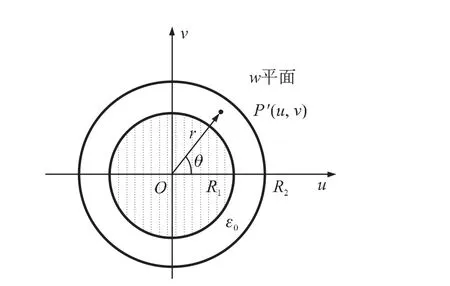
图4 变换后的同心圆环形区域及其内部的场点
3 椭圆柱形电容器内的电场分布
设椭圆柱电容器内、外极板之间的电压为U0,由于保角变换并不能改变内、外极板之间的电压,故变换后的圆柱形电容器内、外极板间的电压仍为U0。
对圆柱形电容器,其中的电场分布是径向的,大小与半径成反比.即

其中A为与电容器两极板之间电压值有关的常数,er为圆柱形电容器横截面上的径向单位矢。
因为
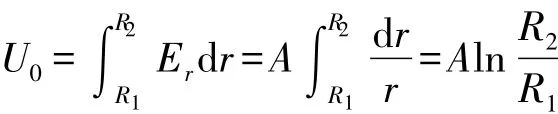
则
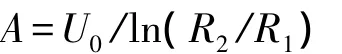
因此,圆柱形电容器内的电场强度分布为

式中eu、ev为圆柱形电容器横截面上沿横、纵轴正向的单位矢。
圆柱形电容器两极板之间的电势分布为(内极板的电势高于外极板)
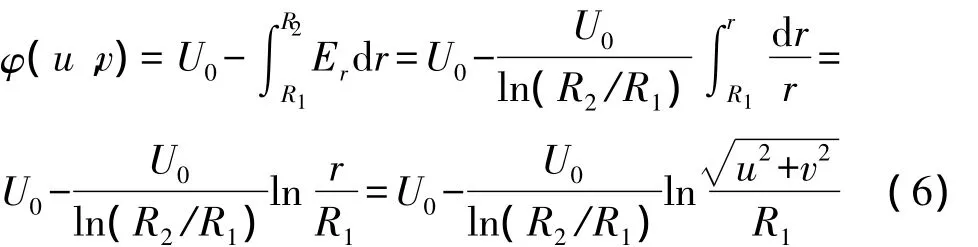
将式(2)代入式(6),有

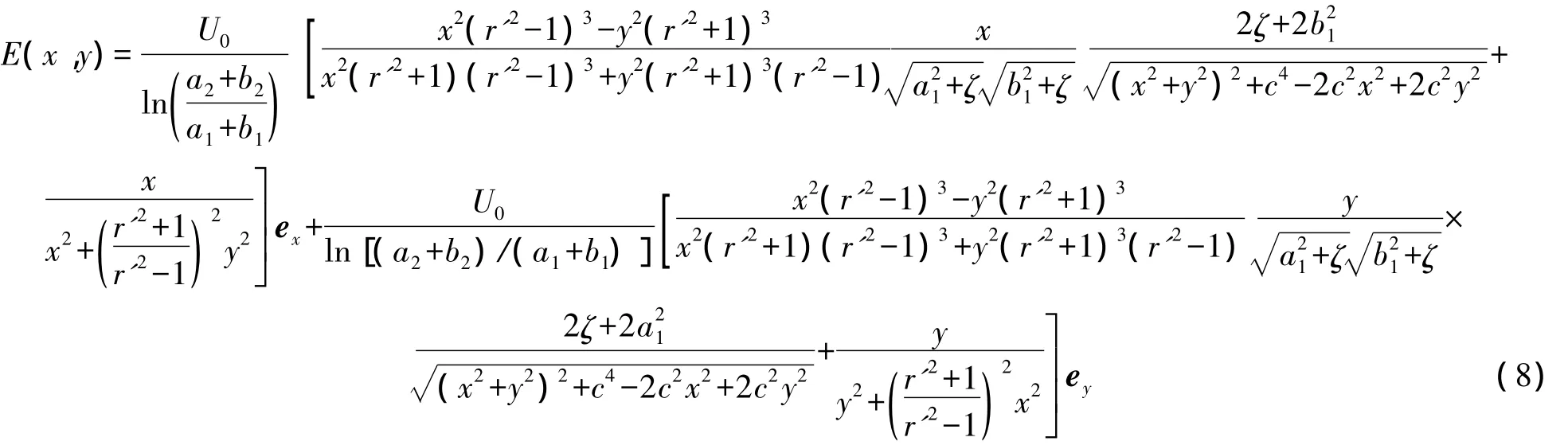
式(7)和式(8)为椭圆柱电容器横截面上的电场分布表达式.其中和 ey分别为沿椭圆柱电容器横截面共焦椭圆半长轴和半短轴方向的单位矢,且 ex=eu,ey=ev。
图5和图6为利用数学软件MATLAB所绘制出的椭圆柱形电容器横截面上电场线与等势线分布图.

图5 椭圆柱电容器内的电场线与等势线(面)图(a1=3 m、b1=2 m,a2=5 m、b2= m)

图6 椭圆柱电容器内的电场线与等势线(面)图(a1=8 m、b1=2 m,a2=9 m、b2= m)
图5和图6中的电场线依相邻电场线间的电通量相同绘制出,而等势线则按相邻等势线间电势差相等画出。图中的电场线与等势面及极板垂直,且在椭圆柱电容器内部,愈靠近内极板表面,电场愈强.内、外极板长轴顶点处的场强要大于极板的其他部位。比较图5和图6可以看出,当电容器极板截面椭圆的焦距增大时,内、外极板长、短轴顶点处场强差增大。作出的图与预期结果相符.图5中a1=3 m、b1=2 m,m;图 6 中a1=8 m、b1=2 m,a2m;两图中电容器极板间的电压均为U0=100 V.
4 耐压能力
由式(8)可知,当x=a1,y=0时,可得到椭圆柱电容器内极板半长轴顶点处的场强为
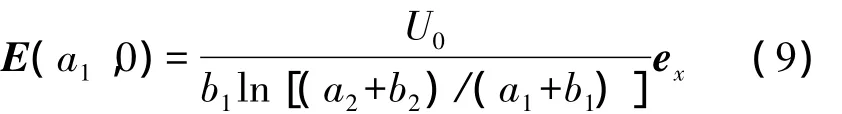
长、短半轴分别为a、b的椭圆的周长的近似值为,由此得该椭圆转换为圆的半径为
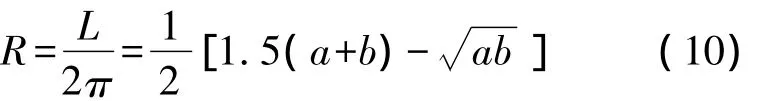
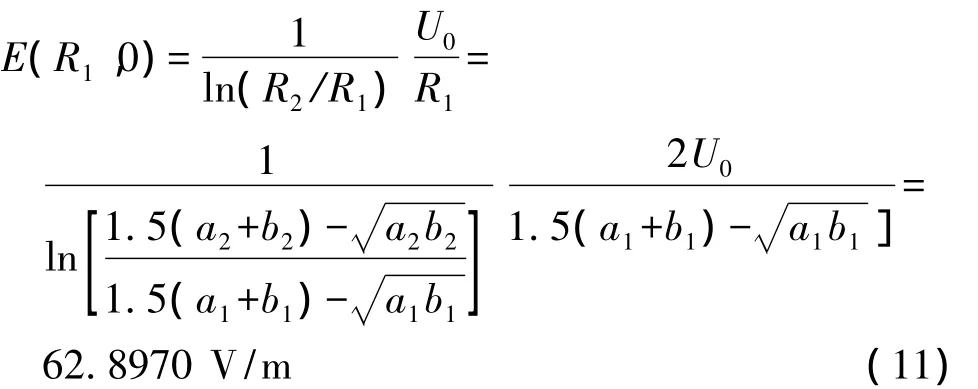
由式(9)又可得变形后的共焦椭圆柱电容器内极板长轴顶点处的场强
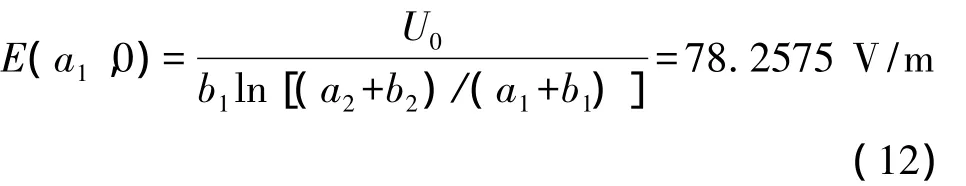
同理,对横截面尺寸如图6的椭圆柱电容器,其变形前内极板表面处的场强为

而变形后的共焦椭圆柱电容器内极板长轴顶点处的场强则为
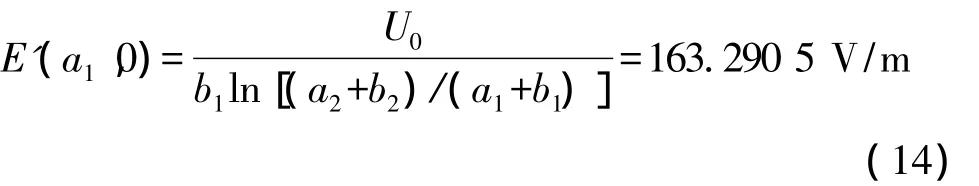
比较式(11)、式(12)及式(13)、式(14)可知,在电源电压一定的情况下,椭圆柱电容器内极板长轴顶点处的场强要大于变形前的圆柱形电容器内极板上表面处的场强,其外极板长轴顶点处的场强也满足此关系。所以,当圆柱形电容器不论由于工艺问题还是由于受力变形,其截面成为椭圆状时,都要导致其耐压能力降低,并且椭圆的焦距越大,耐压能力降低的程度越高。由式(10)可知,截面椭圆长、短半轴分别为a1=3 m、b1=2 m和a2=5 m、b2的椭圆柱形电容器,变形为此形状前对应的圆柱形电容器的截面圆的内、外半径分别为R1=2.525 3 m、R2=4.743 7 m,而截面椭圆长、短半轴分别为a1=8 m、b1=2 m和的椭圆柱形电容器,变形为此形状前对应的圆柱形电容器的截面圆的内、外半径分别为R1=5.5 m、R2=6.975 m。图7和图8为通过数学软件MATLAB分别绘制出的这两组内、外半径数据下的圆柱形容器内的电场分布图。
将图7和图8分别与图5和图6比较可看出,椭圆柱电容器内极板长轴顶点处的电场线(或等势线)密度,要大于变形前的圆柱形电容器内极板表面处的电场线(或等势线)密度,此处场强变大,与式(11)和式(12)计算结果一致。这说明,当圆柱形电容器发生形变而成为椭圆柱形电容器时,其耐压能力将降低。
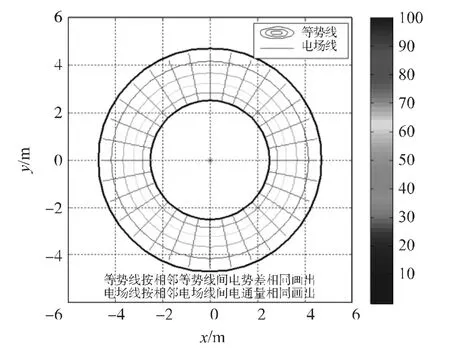
图7 形变前的圆柱形电容器内的电场分布图(R1=2.525 3 m、R2=4.743 7 m)

图8 形变前的圆柱形电容器内的电场分布图(R1=5.5 m、R2=6.975 m)
下面计算极板椭圆化前后圆柱电容器耐压能力的改变量。由式(11)和式(12)可得,在介质的介电强度(即击穿场强)一定的情况下,椭圆柱形电容器所承受的电压Ue要小于同轴圆柱形电容器所承受的电压Uc,在电容器所填充介质相同的情况下,椭圆柱形、圆柱形电容器的耐压能力之比Ue/Uc为

或
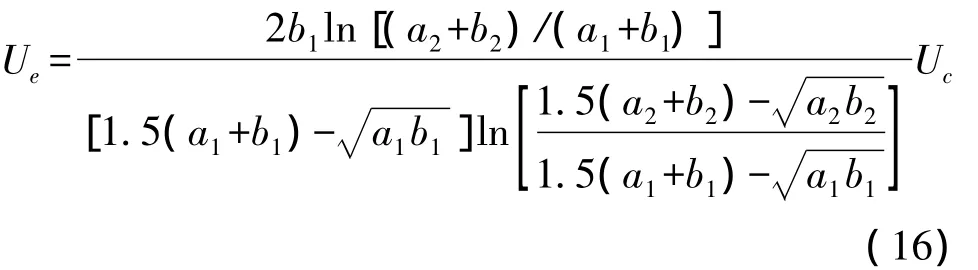
下面根据式(15)给出Ue/Uc随极板椭圆尺寸变化的一组数据,以此来说明椭圆柱形电容器的耐压能力随椭圆尺寸的变化情况。
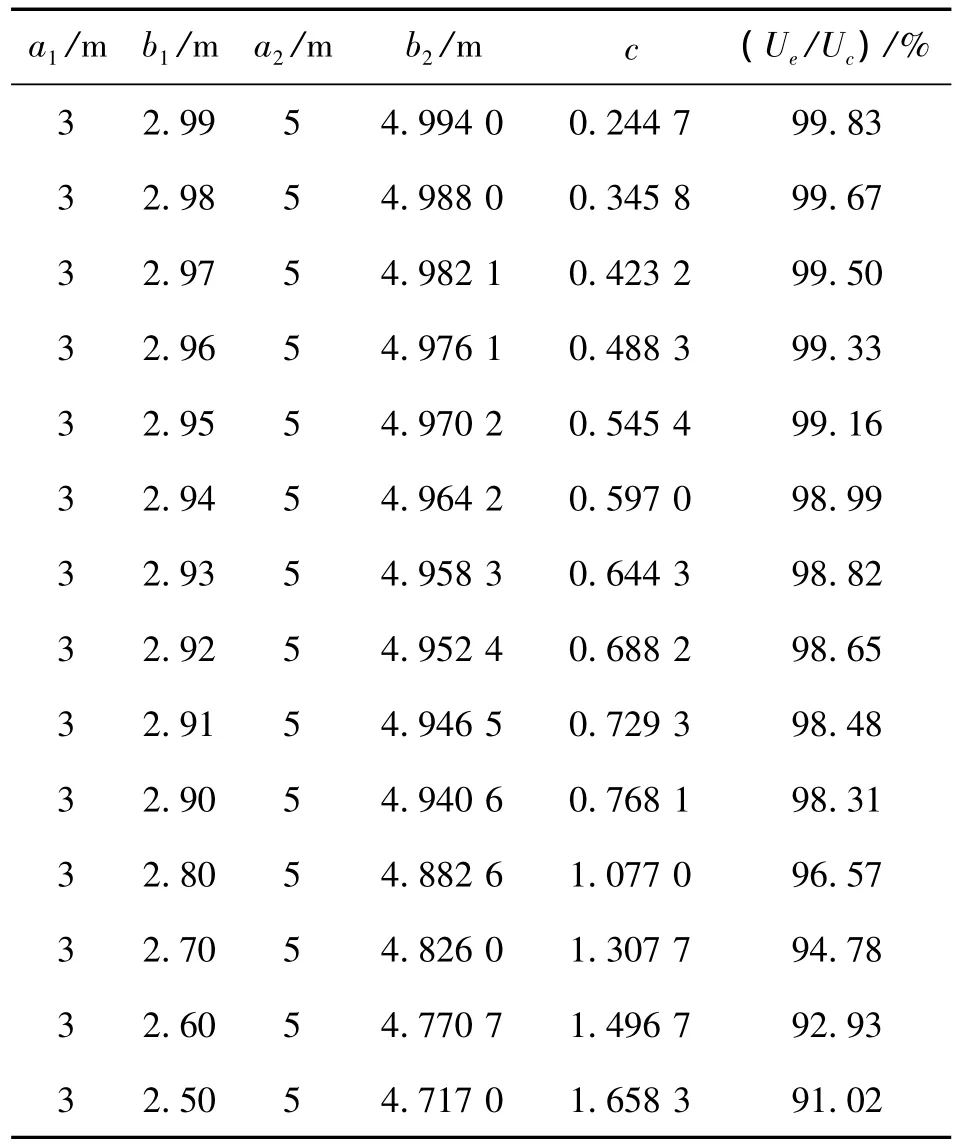
表1 耐压能力Ue/Uc随极板椭圆尺寸的变化
从表1中的数据可以看出,若电容器的内、外极板的椭圆长、短半轴分别为 3 m、2.95 m及 5 m、4.970 2 m,知Ue/Uc=99.16%,即内、外极板的椭圆的半焦距为0.545 4时,该电容器的耐压能力为其同轴时的约 99.16%,取Uc=220 V,则Ue=218.15 V;若电容器的内、外极板的椭圆长、短半轴分别为3 m、2.70 m及5 m、4.826 0 m,知Ue/Uc=94.78%,即内、外极板的椭圆的半焦距为1.307 7时,该电容器的耐压能力为其同轴时的约94.78%,取Uc=220 V,则Ue=208.5 V。显然,圆柱形电容器由于极板截面的椭圆化,将使其耐压能力降低,椭圆化超过一定程度,耐压能力将较大程度地低于工作电压,电容器有被击穿的危险,不能正常工作。
综上所述,圆柱形电容器的横截面由于工艺上出现的椭圆化,将直接影响到电容器的使用寿命和质量。由本文的结论可知,为保证电容器的质量和使用寿命,在生产工艺上要求尽量减小其椭圆化程度,将其需控制在一定范围之内。本文所讨论的为圆柱形电容器的极板截面椭圆化为共焦椭圆的情形,表1中所提供的耐压能力随极板截面椭圆尺寸的变化数据供生产厂家参考。
5 结束语
计算机数值模拟的研究方法已成为继实验研究和理论分析之外的第3种研究手段,本文将理论分析与计算机数值模拟相结合,通过椭圆柱形电容器电场分布的可视化,研究了极板截面椭圆化对圆柱形电容器耐压能力的影响,故所得数据精确度高且可靠,可为一般的电容器的加工制作精度提供理论依据和参考数据,对提高圆柱形电容器的质量,定量计算生产中出现的工艺偏差具有一定的理论价值和实际意义,本文所使用的研究方法也可供电容器研究专业人员在新型电容器的设计和研发方面借鉴。
[1]路宏敏,赵永久,朱满座.电磁场与电磁波基础[M].北京:科学出版社,2006:128-131.
[2]苏东林,陈爱新,谢树果.电磁场与电磁波[M].北京:高等教育出版社,2009:106-109.
[3]焦其祥.电磁场与电磁波[M].北京:科学出版社,2007:168-169.
[4]游荣义.椭圆柱形电容器的电容[J].大学物理,2001,20(12):26-27.
[5]孙春峰.用复变三角函数变换求共焦点椭圆柱形电容器的电势及电容[J].大学物理,2005,24(2):13-15.
[6]贾秀敏.再论共焦椭圆柱形电容器的电场及电容[J].大学物理,2009,28(9):22-24.
[7]郑民伟.共焦椭圆柱形电容器的电场和电容的另一种计算[J].大学物理,2011,30(9):31-33.
[8]刘世忠.用双能量法计算椭圆柱形电容器和偏心电缆的电容[J].福州大学学报(自然科学版),1992,20(3):43-48.
[9]张丽,张健.利用微元法求电容器电容[J].长春师范学研学报(自然科学版),2009,28(5):15-16.
[10]林焰清,陈钢.线电荷与接地椭圆柱形导体系统的电势[J].大学物理,2009,28(8):25-27.
