数学归纳推理思维的有效培养

小学生的数学思维大多以直接经验为主，需要具体形象思维和抽象逻辑思维相结合来促进其认知学习的提升。因此，对于数学概念、数学法则、数学运算律、数学公式的学习都离不开具体的直观形象，当然更离不开抽象的归纳思维能力。小学阶段归纳推理作为一种重要的思维过程，要促进学生对于其的掌握，教师要善于运用观察、分析与比较、分类、抽象与概括等思维方法。

一、观察

观察，简言之就是通过观察事物的特征以及各事物之间的关系，以便获得对事物规律性的认识。

例如：一组数如下：找规律填数：

6，12，18，24，（ ），（ ），（ ）

8，16，24，32，（ ），（ ），（ ）

9，18，27，36，（ ），（ ），（ ）

观察数字的规律，第一组数字：后一个数都比前一个数大6，归纳推理可知，第五个数比第四个数大6，因此类推24+6=30，30+6=36，36+6=42，得出答案为30，36，42。第二组数字：后一个数都比前一个数大8，归纳推理可知，第五个数比第四个数大8，因此类推32+8=40，40+8=48，48+8=56，得出答案为40，48，56。第三组数字：后一个数比前一个数大9，归纳推理可知，答案为：45，54，63。

观察不是毫无目的，毫无章法的。在解答此类型的题目时，教师要引导学生有顺序的进行观察，培养起归纳推理的思维能力。

二、分析与比较

分析与比较在归纳推理中起着很重要的作用，学生要掌握试题的规律以及对试题进行正确的解答，必须经过认真仔细的分析比较。那么教师如何引导学生进行分析与比较呢？

例如：有一组数的运算结果如下：

11×11=121，11×12=132，11×13=143，11×14=154，

请问同学们，你们发现这组数有什么规律，你们能在1分钟内计算出下列试题吗？11×15=（ ），11×16=（ ）11×17=（ ），11×18=（ ）。

首先，我们通过分析与比较每组数的特点可以得出：第一个乘数都为11，第二个乘数的十位都为1，且都是两位数。其次，结果都为三位数，且经过进一步的分析比较这个三位数的特点，可以得出结论：三位数的百位与各位与第二个乘数相同，十位等于百位与个位相加的和。显然，通过分析与比较，这类试题就变得相当的简单了，学生可以很快得出答案：11×15=（165），11×16=（176），11×17=（187），11×18=（198）。

三、分类

分类是在分析、比较的基础上，经过抽象、概括而获得的对于学习对象的更进一步的认识。通过分类，可以使杂乱无章的现象条理化、清晰化，甚至可以在不同事物之间起建立联系。因而，分类对于数学的学习有很重要的价值。例如：

有一张日历表如上图所示：认真观察方框中的五个数，并回答下列问题：

（1） 阴影部分中中间数与周围四个数有什么关系？

（2） 假设中间数是x，那么它的左边数是__，它的右边数是__，上边数是__，下边数是__。

对于此题的解答，教师可以引导学生进行分类的归纳思维训练解答。

第一类：横向数，观察可以得出：为一组连续的数，因此左边数为x-1，右边数为x+1。

第二类：纵向数，分析与比较可以得出：前一位数与后一位数相差为7，因此上边数：x-7，下边数为x+7。

四、抽象与概括

由于数学知识本身是较为抽象的，所以在数学归纳推理的思维训练中，往往用概括方法将抽象概念，公式等以形式化表现出来。抽象与概括的思维能力培养，可以促使学生将抽象的、深奥的知识加以形象化、简单化、生活化的理解。

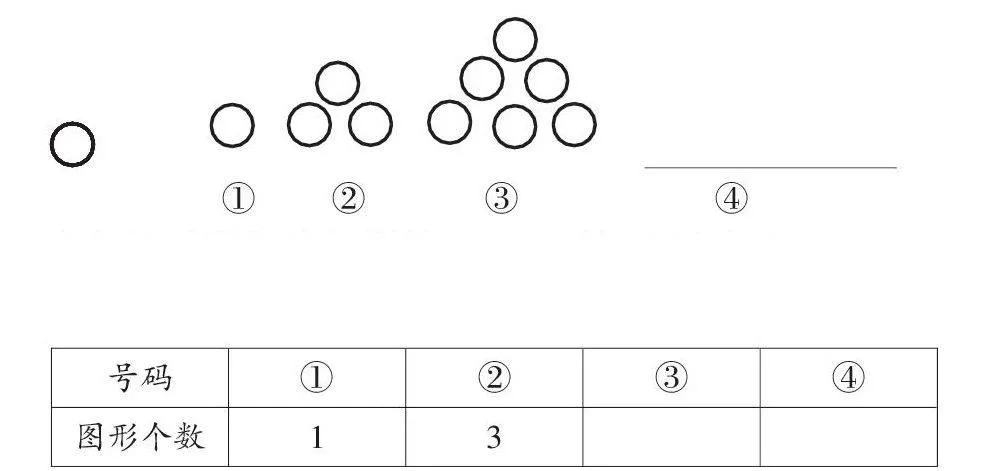
（1） 请同学们找找规律，画一画第四个图形。

（2） 请把下列表格补充完整。

此题的解答，有一定的难度，它需要学生具有一定的抽象与概括的思维。通过把图形转化为数字，可以概括其规律为：每一号码底层的圆圈数和等于号码所对应的数（如：①号码所对应的数为1）。而该每一号码的圆圈总数为上一号码的总和加上自己的号码数。②的圆圈总数等于①号码所对应的1加上底层圆圈数和2，简而言之，②的总和数：1+2=3，所以，③的总和数：3+3=6；④的总和数：6+4=10。

归纳推理思维是数学学习中重要的思维方式之一，归纳智慧的形成是一个循序渐进的过程，对它掌握在一定程度上有利于深化、细化对数学课程的认识，当然对于数学归纳推理的理论与实践，在教学中仍需改善、深化。

（责编 阮 妮）