星载GPS接收机RAIM算法性能及参数影响分析

隋叶叶 柳涛

（航天恒星科技有限公司，北京 100086）

1 引言

在GPS导航系统中，导航卫星的故障可能会造成伪距观测值偏差较大，从而影响定位精度。为提高GPS导航系统的完好性，接收机在进行测量的同时，必须兼顾伪距观测值偏差对测量值的影响，接收机自主完好性监测（RAIM）便是接收机对导航定位结果进行实时质量控制的一种算法。

RAIM 算法要完成两步检测：首先，检测当前可视卫星的几何条件是否可以进行粗差（没有模型化的偏差）的检测和排除，即判断RAIM 算法是否可用；当RAIM 算法可用时，进一步检测是否有故障发生，即进行粗差的检测和排除。因此，可用性、故障检测的灵敏度与可靠性，可作为衡量RAIM 算法性能的标准。另外，RAIM 算法的两步检测都是以数理统计的可靠性理论为基础的假设检验，伪距测量误差标准差、漏警概率、误报概率及定位告警限值等先验参数的选择，将直接影响到算法的可用性及完好性监测性能，因此，参数的选取至关重要。

目前，对RAIM 算法的实现方法研究较多，主要侧重于提高可用性及故障检测能力。但是，对于RAIM 算法能够检测的最小偏差及不可检测偏差对定位结果的影响，还没有理论可循；对于先验参数与RAIM 算法性能之间的影响关系，也没有专门的文献介绍；国内还没有在轨RAIM 算法应用的案例。因此，为了在相应的可靠性及可行性要求下，对RAIM 算法中的参数配置做到有据可循，定量、全面地认识参数取值对RAIM 算法的影响，是十分必要的。本文基于VC＋＋6．0实现的RAIM 算法仿真平台，研究了在不同的可靠性需求及测距精度条件下参数的适当选取，可为工程上RAIM 算法的参数选取提供参考。

2 RAIM 算法性能分析

目前，对RAIM 算法理论和算法仿真的研究比较成熟，但是针对星载GPS接收机的可用性、灵敏度和可靠性的研究还很少。本节在对RAIM 算法进行简要介绍之后，重点针对高动态星载应用中的3种性能进行分析。

2．1 RAIM 算法简介

观测值的误差可通过伪距残差反映出来，利用数理统计的假设检验分析残差，能检查系统中是否存在粗差。根据此原理，RAIM 算法的流程如图1所示。

图1 RAIM 算法流程Fig．1 Flow diagram of RAIM algorithm

在卫星几何条件不佳时，某颗卫星尽管会产生较大的定位误差，但单位权中误差却很小，可能会导致漏警；因此，必须在卫星的几何分布满足一定条件时，才能应用RAIM 算法。如图1 所示，将反映卫星几何分布的PPL值与PAL 值比较，在PPL 值不超过PAL值时，判定算法可用，解算的星历与测量数据作为输入进行故障检测。定位后，伪距残余在一定程度上提供了伪距测量值和定位质量好坏的一些信息，某颗卫星上伪距粗差的出现，会在相应的伪距残余分量中有所体现，因此，通常选取该量作为检测统计量。根据统计量所服从的统计分布，在满足系统所要求的误报概率条件下，通过一定的变换关系确定检测门限。统计量超过检测门限，说明有故障卫星存在，要进一步识别故障卫星。

2．2 可用性判别

利用RAIM 算法进行故障检测，只有当可视卫星数足够（n≥5）时，才会有效。即使所有GPS卫星都正常工作，仍然有很多区域的卫星几何条件不够理想。这种较差的几何条件，也许对导航定位是足够的，但是无法保证以较高的概率发现错误观测。因此，在故障检测之前，首先要判定卫星几何条件是否满足故障检测的要求，即要给出完好性保证。

2．2．1 卫星特征性斜率

在GPS导航系统的定位解算过程中，最难检测的卫星就是其偏差能产生最大斜率的卫星，下面对单颗卫星故障时检测统计量与定位误差的关系进行分析，并引入卫星特征性斜率的概念。

n颗可视卫星的伪距观测值误差模型可表示为［1］

式中：伪距残余y为n×1的测量矩阵，代表实际测量伪距与预测伪距的差值；H为n×4的由状态空间向测量空间的转移矩阵；x为用户实际位置的3 个分量和接收机时钟偏差，是4×1的状态矩阵；ε为n×1的矩阵，表示观测伪距噪声。

忽略正常误差的影响，假设第i颗卫星存在偏差bi，这时误差可表示为ε＝［0 …bi… 0］T。容易得出，由偏差bi产生的空间位置定位误差为

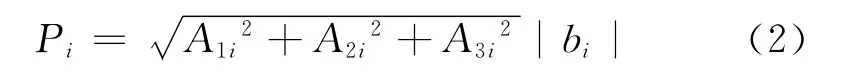
式中：A1i，A2i，A3i分别为矩阵A＝（HTH）-1HT的第1、2、3行第i列元素。

定义伪距残差向量w为实际测量值与期望测量值之差，表示为［2］

式中：矩阵S＝I-H（HTH）-1HT，I为单位阵。

若检测统计量定义为残差平方和，则根据映射矩阵S的特性，在上述偏差的情况下，检测统计量为

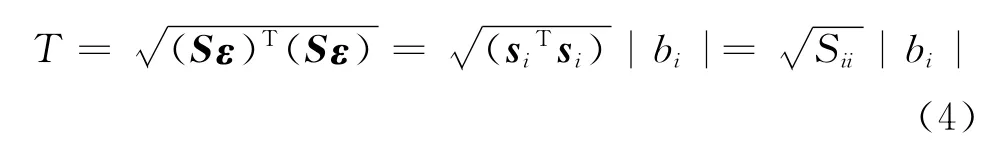
式中：si为矩阵S的第i列；Sii为矩阵S的第i行i列对角线元素。

由第i颗卫星故障引起的定位误差与检测统计量有如下关系。

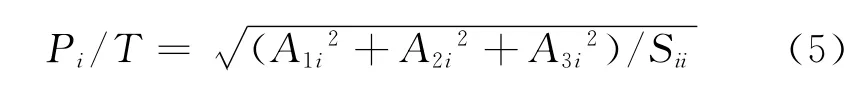
式（5）反映了单颗卫星伪距发生偏差时，检测统计量与定位误差之间成线性关系，而与故障大小无关。若把该量对应于卫星特征性斜率，则能够表征该卫星对故障的反应灵敏度。对于给定的误差，斜率最大的卫星，检测统计量最小，是最难检测的。基于卫星特征性斜率的概念，若最难检测故障的卫星，不能保证系统所要求的漏警概率要求，那么RAIM算法在这种卫星几何分布情况下不可用。可以证明有如下关系成立［3］。

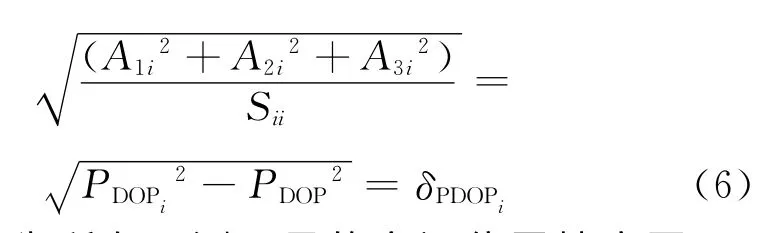
式中：PDOP为所有观测卫星的空间位置精度因子；PDOPi为去掉第i颗卫星后的空间位置精度因子；δPDOPi为第i颗卫星的空间位置精度因子变化，即卫星特征性斜率。

2．2．2 精度因子变化限值

根据数理统计理论，在有故障卫星情况下，检测统计量服从非中心化参数为λ的卡方分布。

式中：SSE为残差平方和；σ0为等效测距误差。

无伪距故障时，如果出现告警，则为误报。因此，给定误报概率PFA，应有如下概率等式［4］。

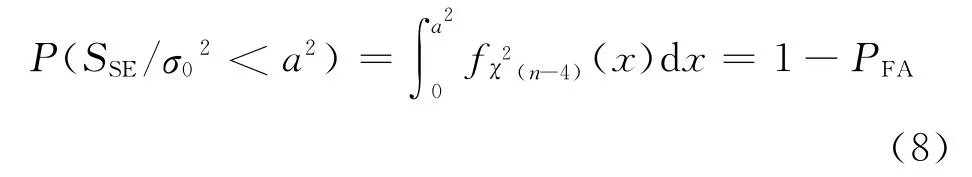
式中：a为检测限值；χ2为卡方分布。

通过式（8），可确定SSE／σ02的检测限值a。卫星存在故障时，检测统计量SSE／σ02应大于a2；若SSE／σ02小于a2，则为漏警。给定漏警概率PMD，应满足式（9）。

由式（9）可得非中心化参数λ。在式（7）中，若Pi以PAL值（表示为PAL，由系统需求给出或用户自己定义）代替，可得空间位置精度因子变化限值为

在故障检测前，实时计算各颗卫星对应的δPDOP值，并取其中的最大值为δPDOPmax，若δPDOPmax＜δPDOPT，表示在一颗卫星出现故障且为最难检测的卫星时，能够保证漏警概率要求，即RAIM 算法可用。

2．3 估计的灵敏度

灵敏度包括内灵敏度和外灵敏度，用来衡量RAIM 算法能够发现单个模型误差的能力，以及不可发现的模型误差对平差结果的影响，体现了RAIM 算法检测和识别粗差的能力，另外，外灵敏度体现了RAIM 算法对定位结果的保护程度。

2．3．1 内灵敏度

从第2．1节的分析得出，若给定误报概率和漏警概率，可得非中心化参数λ，然后利用式（7）计算每颗卫星的偏差bi，即

bi的最小值就是内灵敏度，也就是最小可检测粗差。因此，在GPS定位中，给定误报概率和漏警概率，可用式（11）计算出每颗卫星的内灵敏度。内灵敏度由误报概率、漏警概率、卫星的几何条件和等效测距误差决定，会随非中心化参数λ的增大而增大，即提高误报概率和漏警概率，是以降低内灵敏度为代价的。

2．3．2 外灵敏度

如果观测值Li的粗差值小于bi的最小值，在给定的误报概率和漏警概率下，该粗差将不被发现，会对参数解产生影响，即

式中：li为第i颗卫星的影响矩阵，其长度即为外灵敏度的长度；Δxi，Δyi，Δzi分别为测量误差引起的第i颗卫星x轴、y轴和z轴方向上的定位误差；c为光速；Δti为测量误差引起的第i颗卫星定时误差。

将式（12）的结果转到站心坐标系下，即

式中：ΔEi，ΔNi，ΔUi分别为测量误差引起的站心坐标系下东向、北向、天向的定位误差；R为旋转矩阵。

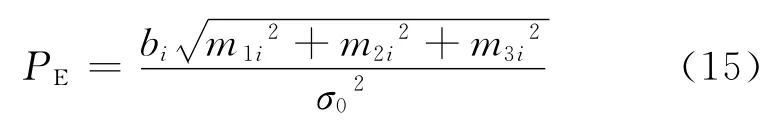
式中：m1i，m2i，m3i分别为矩阵M的第1行、第2行和第3行的第i列元素。

这种不可检测的故障引起的最大定位误差，称为外灵敏度。

2．4 应用的可靠性

可靠性表明算法的可靠程度，它是RAIM 算法应用中的一项基本性能评估指标，即RAIM 算法能够正确检测出故障状态的概率，通常用粗差探测率来表征。粗差探测率定义为观测值中含有粗差并能够被检测出来，即正确探测粗差的历元数与包含粗差的总历元数的比值［5］。由于该性能的评估较简单、直观，因此本文不再作详细介绍。

3 实测数据仿真

3．1 数据特性分析

观测数据采用2012年2月1日某卫星的在轨实测数据，数据提供CA 码及L1载波相位测量值，采样间隔为1s，观测历元取3600s。导航文件采用国际全球卫星导航系统服务（IGS）提供的同一天的广播星历，星历每2h更新一次。以事后处理所得的精密定轨数据作为基准值，各历元的可视卫星数与空间位置精度因子（PDOP）值曲线如图2所示。

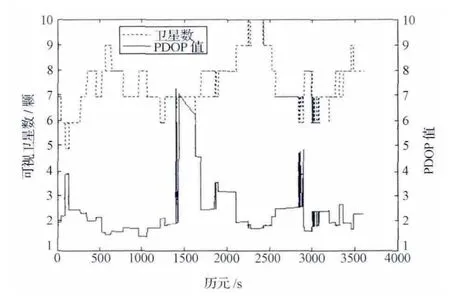
图2 可视卫星数与空间位置精度因子值Fig．2 Visible satellite numbers and PDOP value

从图2可以看出，各历元的可视卫星数在5～10颗之间，均能满足RAIM 算法进行故障检测的可视卫星数要求。

3．2 场景设计

由于RAIM 算法的可用性、灵敏度直接受到卫星的几何条件、误报概率、漏警概率、等效测距误差等多个参数选择的限制，而误报概率、漏警概率及等效测距误差又是要在故障检测之前给出的先验量；因此，这些先验参数的确定至关重要，将直接影响到RAIM 算法的性能。

以下从定位系统和用户两个层面来分析各种测距误差的来源。系统层面主要受制于卫星轨道与钟差产品误差［6］；用户层面受制于用户接收设备和观测环境，观测环境包括大气延迟误差（电离层、对流层误差），不同类型的接收机在不同观测环境下得到的观测值精度不同［7-8］。下面给出2组统计结果作为仿真的参考输入。

1）第1组统计结果

一种接收机典型的伪距测量误差分布，见表1［9］。

表1 接收机的典型伪距测量误差Table 1 Typical pseudorange measurement errors of receiver

表1列出的误差值均为整数，它反映了对真实值的不确定性。在RAIM 算法应用中，用户可以根据自己的实际测量情况，对误差模型作更精确的改进。

2）第2组统计结果

文献［10］中利用单点定位精度影响评估与分析软件，统计得到中国区域在2009年101天的空间信号距离误差（SISRE）、电离层改正误差等测距误差的均值结果，见表2。

表2 中国区域伪距测量精度综合影响分析Table 2 Pseudorange measurement accuracy impact analysis in China area

为了较全面评估卫星的几何条件和等效测距误差对RAIM 算法性能的影响，本节基于表1和表2中对测距误差统计的分析，设计了表3中的2种不同场景，分别评估2种场景下在轨RAIM 算法的可用性、灵敏度和可靠性。其中，误报概率和漏警概率是根据经验值与航空上的参考提出的要求［11］。

表3 RAIM 算法场景设计Table 3 Scene design of RAIM algorithm

3．3 星载RAIM 算法性能及参数影响研究

在2种不同场景下，模拟计算卫星接收机对不同GPS导航卫星的内、外灵敏度，并分别通过设置告警限值、为测量值引入模拟粗差，对RAIM算法的可用性及可靠性进行研究。

图3 为 该 卫 星 在2012年2月1日GPS 时00：00：00时刻场景1和场景2下的灵敏度。其中：PE是内灵敏度对定位结果的影响。

从图3可以看出，此时刻的可见GPS卫星数为7颗。场景1中，误报概率和漏警概率分别为0．05%和0．1%，测距误差为6 m 时，其内灵敏度为26～39m。当观测值中的粗差值小于内灵敏度时，粗差不能被发现，无法检测出的粗差对定位的影响为6．9～37．2m。在降低漏警与误报要求，且提高测距精度后，即在场景2 中，不同卫星的内灵敏度为8～18m，不可检测的粗差对定位结果的影响最大在14．85m。场景2比场景1的检测灵敏度提高，是以牺牲可靠性为代价的。可见，先验概率的选取，将直接影响到RAIM 算法内、外灵敏度。在工程应用中，应根据实际需要，权衡可靠性、可用性与灵敏度的重要性，确定适当的参数。

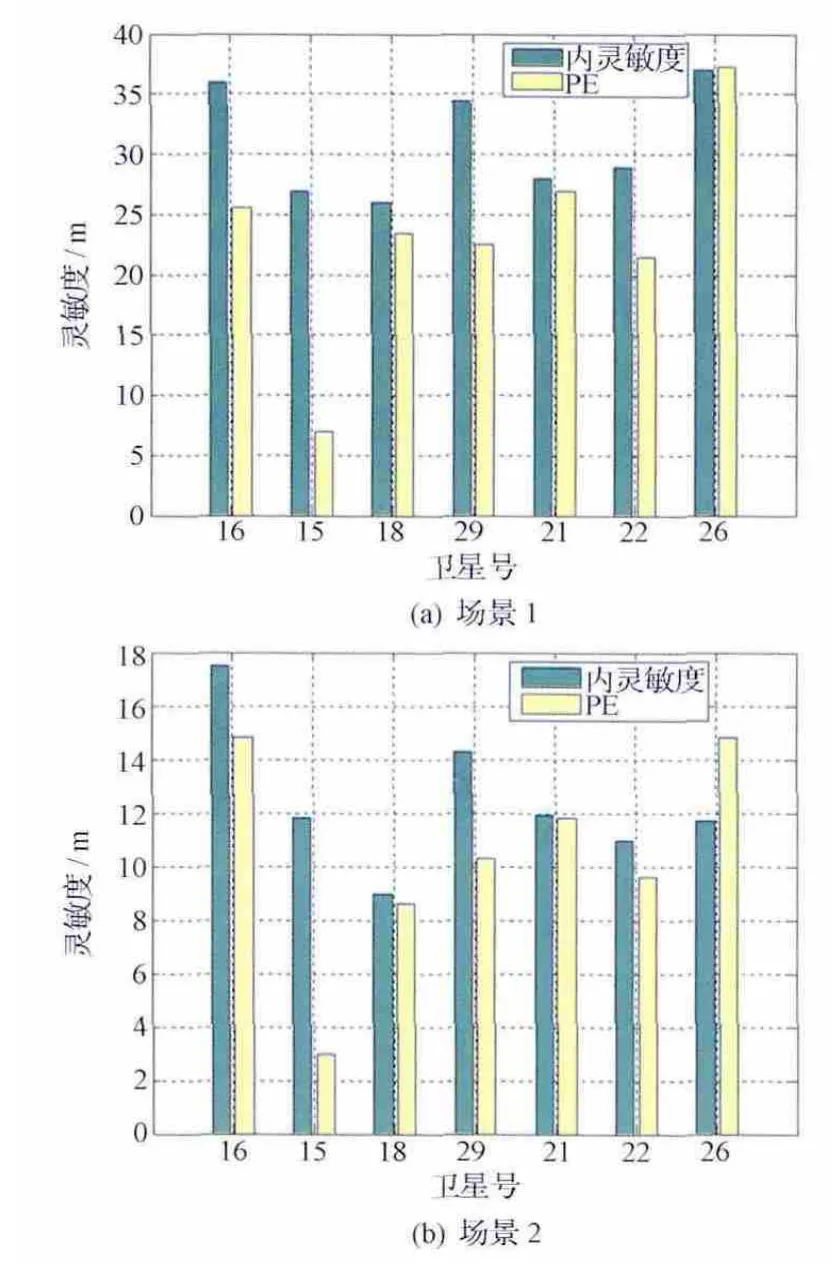
图3 2种场景下的灵敏度Fig．3 Sensitivity in two scenes

表4列出了在2种场景中分别设置不同的PAL值和添加不同的模拟粗差时，RAIM 算法的可用性及故障探测率。

从以上算例可以看出：在2 种场景中，若PAL取300m，可以保证90%的RAIM 算法可用性；在场景1中，由于误报概率和漏警概率要求严格，测距误差定得较高，故障探测率较低；在场景2中，误报概率和漏警概率放宽，对于20m的测量误差，能够保证超过80%的故障探测率。

表4 RAIM 算法可用性及故障探测率Table 4 Availability and fault detection probability of RAIM algorithm %

综上所述，可用性、灵敏度和可靠性是相互制约的，一种性能的提高，往往以另外一种性能的降低为代价。在工程应用中，对于RAIM 算法可用性要求比较严格的场合，为了减小RAIM 算法空洞，应合理降低对漏警概率的要求，并且提高观测数据的精度。为了保证98%的可用性，漏警概率指标不得低于0．010 0，观测数据精度也应控制在3m 以内。对于故障检测可靠性要求严格的场合，应提高测距精度，同时合理降低对内灵敏度的要求。为保证85%的故障检测可靠性，内灵敏度一般不超过25 m，并且观测数据精度应控制在6m 以内。

4 结束语

本文针对星载GPS接收机RAIM 算法的性能及参数的影响、选取进行了分析。RAIM 算法的可用性、灵敏度与可靠性，均受到先验误报概率和漏警概率要求的制约，灵敏度的提高要以可靠性的降低为代价，而可用性则受到定位告警限取值的限制，提高算法的可用性要以降低定位精度要求为代价。本文设计了2种适合于高动态在轨应用环境的参数场景，试验结果表明，在不同场景下，RAIM 算法具有相应不同的性能。因此，在工程应用中，应根据用户／系统提出的具体性能指标要求，选择合理的先验参数。在后续的研究中，要建立仿真验证系统，对多星故障进行分析。同时，探索星座完好性算法，为进一步提高中国卫星导航系统的性能积累经验。

（References）

［1］陈小平，滕云龙．接收机自主完好性监测算法研究［J］．电子科技大学学报，2008，37（2）：218-220

Chen Xiaoping，Teng Yunlong．Study of receiver autonomous integrity monitoring algorithm［J］．Journal of University of Electronic Science and Technology of China，2008，37（2）：218-220（in Chinese）

［2］党亚民，秘金钟，成英燕．全球导航卫星系统原理与应用［M］．北京：测绘出版社，2007

Dang Yamin，Mi Jinzhong，Cheng Yingyan．Principles and applications of global navigation satellite system［M］．Beijing：Surveying and Mapping Press，2007（in Chinese）

［3］郭睿，郑勇，杜兰．GPS和Galileo系统下RAIM 算法可用性分析［J］．测绘科学技术学报，2006，23（6）：448-453

Guo Rui，Zheng Yong，Du Lan．Analysis on RAIM availability of different navigation systems［J］．Journal of Geomatics Science and Technology，2006，23（6）：448-453（in Chinese）

［4］刘准，陈哲．GPS自主式完整性检测技术研究［J］．北京航空航天大学学报，2003，29（8）：673-676 Liu Zhun，Chen Zhe．Study on GPS receiver autonomous integrity monitoring［J］．Journal of Beijing University of Aeronautics and Astronautics，2003，29（8）：673-676（in Chinese）

［5］丁克良，欧吉坤．基于拟准检定法的GPS接收机完备性检验算法［C］／／第三届中国国际数字城市建设技术研讨会．北京：中国建筑学会，2007：316-319

Ding Keliang，Ou Jikun．A new algorithm for GPS receiver autonomous integrity monitoring based on quasiaccurate detection of gross errors［C］／／Proceedings of the 3rd China International Digital Technology Symposium on Urban Construction．Beijing：Architectural Society of China，2007：316-319（in Chinese）

［6］Wang J．Stochastic modeling for real-time kinematic GPS／GLONASS positioning［J］．Journal of the Institute of Navigation，1999，46（4）：297-305

［7］Kenselaar T F．Estimation of the stochastic model for GPS code and phase observables［J］．Survey Review，2000，35（2）：441-454

［8］Gerdan G P．A comparison of four methods of weighting double-difference pseudorange measurements［J］．Trans Tasman Surveyor，1995，1（1）：60-66

［9］罗鸣，曹冲，肖雄兵．全球定位系统——信号、测量与性能［M］．北京：电子工业出版社，2008

Luo Ming，Cao Chong，Xiao Xiongbing．Global Positioning System-signals，measurements，and performance［M］．Beijing：Publishing House of Electronics Industry，2008（in Chinese）

［10］叶世榕．GPS非差相位精密单点定位理论与实现［D］．武汉：武汉大学，2002

Ye Shirong．Theory and implementation of GPS precise point positioning using undifferenced phase［D］．Wuhan：Wuhan University，2002（in Chinese）

［11］International Civil Aviation Organization（ICAO）．The Chicago convention on international civil aviation［S］．Montreal，Canada：ICAO，2001