巴东县人工针叶同龄混交林直径分布拟合研究

张 峰，石军南，张丹华，吴 疆

（中南林业科技大学，湖南 长沙 410004）

巴东县人工针叶同龄混交林直径分布拟合研究

张 峰，石军南，张丹华，吴 疆

（中南林业科技大学，湖南 长沙 410004）

基于巴东县国有林场人工针叶同龄混交林标准地的调查数据，采用三参数威布尔分布函数（Weibull）、正态分布函数、伽玛分布函数及对数正态分布函数拟合林分的直径分布，并结合卡方（λ2）检验，试图建立能够准确描述人工针叶同龄林林分直径分布规律的函数和参数，再通过建立的分布函数预测和分析林分径阶株数分布。结果表明：4种分布函数拟合林分直径分布的拟合效果Weibull分布明显优于其余3种分布函数，用Weibull分布拟合效果最好，精度高，能很好地描述针叶同龄混交林直径分布规律；研究发现Weibull分布函数参数a=5.0、b=12.132 3、c=1.821 3时，可以较准确地预测人工针叶同龄混交林林木株数；经过对林分直径株数分布预测结果分析，证明了函数的准确性和适用性较好。根据Weibull分布函数调整林分株数分布，对于提高林分质量、增强林地生产力具有一定的参考价值。

针叶混交林；同龄混交林； 分布函数；直径分布；拟合效果

林分直径分布是林分内各种大小直径林木按径阶的分布状态[1]，是林分调查和开展森林经营活动最基础的信息。长期研究证明，不论是天然林还是人工林，在未遭受破坏的情况下，林分内部都存在一些比较稳定的结构规律，比如直径分布规律。对于人工针叶混交林，各林木之间由于立地条件不同，使得它们在大小、形状等各方面都必然会产生某些差异，而这些差异在正常情况下会相当稳定地遵循一定的规律[2]。对于这些规律的研究目的，即在于预见和控制[3]。无论在理论上还是在实践上，林分直径分布是最重要、最基本的林分结构。林分直径分布情况对森林经营活动起着指导性作用，通过观测林分直径分布的变化可以确定森林抚育方式[4]。本研究通过标准地调查数据，利用分布函数对人工针叶同龄混交林林分直径结构进行拟合分析，为合理调整巴东县人工针叶同龄混交林林分结构、提高其经济及生态效益提供依据[5]。

1 研究区概况

研究区设在湖北省巴东县巴山林场。巴山林场位于东经 110°04′～ 110°32′，北纬 30°13′～ 31°28′。林场面积 4 660.6 hm2，活立木蓄积302 303万m3，海拔175～1 942 m，年平均气温9～10 ℃，年降水量1 800～2 100 mm，无霜期205 d。土壤为鄂西南山地黄棕壤，平均厚度60 cm。巴东林场主要树种有巴山松Pinus henryi、杉木Cunninghamia lanceolata、柏木Cupressus funebris、日本落叶松Larix kaempferi、柳杉Cryptomeria japonica及其少量漆树Toxicodendron vernicifluum 和硬、软阔树种，以人工中龄林为主。林场属于以保护为主的生态公益型林场，境内森林资源丰富，森林覆盖率为77.02%。

2 材料与方法

2.1 样地数据获取

在研究区选取20年生人工针叶混交林为研究对象，在林区内采用典型抽样技术设置面积为0.2～0.3 hm2的标准地，根据不同地理位置及针叶树种混交类型选取10块标准地，其中8块标准地用来确定分布函数参数，2块标准地用来检验得出的分布函数参数的准确性。地理位置选择方面，考虑到试验区林分相对集中，因此标准地设置为立地条件比较相近的小班。针叶树种类型选择方面，考虑到林场主要以针叶混交林分为主，因此标准地设置在至少有2种针叶混交而且是人工同龄的小班内。标准地林分年龄采用主要树种的年龄，选取主要树种为20年生的人工针叶林的小班设置标准地。标准地调查要素为立地条件和林分特征，主要包括地形地貌、坡度、坡向、土壤、植被及每木检尺，对样地内胸径≥5.0 cm的所有林木分树种实测其胸径等各项因子。

2.2 研究方法

选择合适的概率密度函数，对直径分布模型的建立和使用起着至关重要的作用。本研究选用Weibull分布函数、正态分布函数、伽玛分布函数及对数正态分布函数分别描述人工同龄针叶混交林直径分布规律，并运用λ2检验法对直径分布拟合进行检验。通过检验得出最适合描述人工针叶同龄混交林直径分布的分布函数，并计算其参数值。

2.2.1 威布尔分布函数

Weibull分布是由瑞典物理学家W.Weibull提出，现已成为林分结构模型研究中一种重要的分布，它对直径分布能进行很好的拟合[6]。三参数威布尔分布的概率密度函数为：

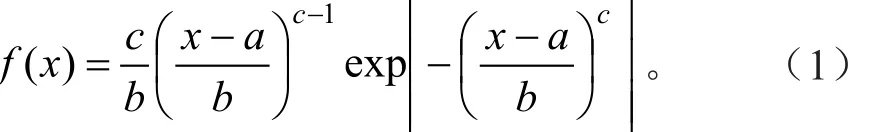
式中：参数a为位置参数，在研究林木直径分布时一般取最小径阶的下限；参数c是Weibull分布中具有实质意义的参数。当c＜1时，为反J型分布函数；当1＜c＜3.6时，为单峰左偏山状分布；当c=1时，为指数分布；当c=2时，为λ2分布；当c=3.6时，为近正态分布；当c→∞时，变为单点分布[5]。

参数经计算后，各径阶理论株数计算公式为：

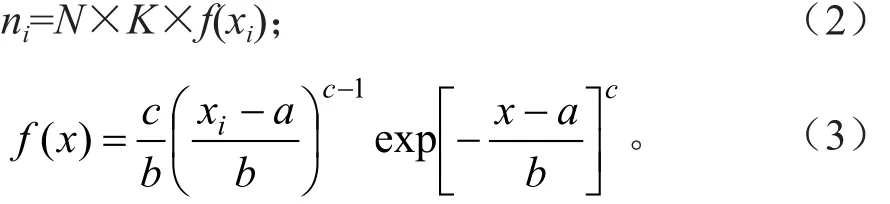
式中：xi为径阶；N为样地总株数；K为径阶距；ni为理论株数。

2.2.2 正态分布函数

正态分布函数的概率密度函数为：

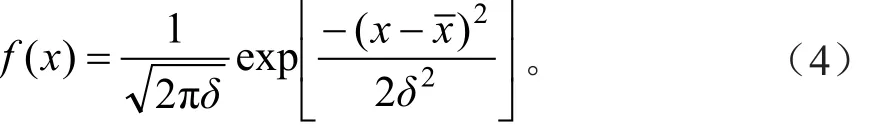
式中：x为随机变量x的数学期望；σ为随机变量x 的标准差[7-8]。

2.2.3 伽玛分布（Gamma）函数

伽玛分布函数的概率密度函数为：

式中：a为最小值；b为尺度参数；c为形状参数。

2.2.4 对数正态分布

对数正态分布的概率密度函数为：

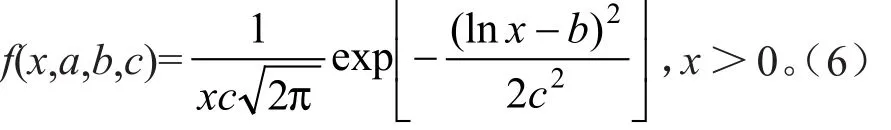
式中：b为log（x）的平均数；c为log（x）的标准差。

2.2.5 分布检验

将4种分布函数进行实际拟合，并对它们各自的理论株数与实际株数在α=0.05的显著水平下作λ2检验，即：

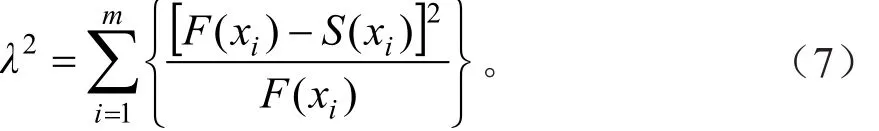
式中：F（xi）表示第i径阶的理论株数；S（xi）表示第i径阶的实际株数；m表示径阶数[9]。

3 结果与分析

3.1 巴山林场人工针叶同龄混交林林分径阶结构特征

根据标准地调查，巴山林场人工针叶同龄混交林林分平均胸径为15.3 cm，变动范围为5.0～36.0 cm；平均树高为10.5 m，变动范围为3.0～18.0 m。不同标准地各径阶株数分布见图1。其直径结构相对简单，基本规律都是6径阶到20径阶的林木株数在林分中所占比重最大；径阶分布的离散程度大，虽然林木多数集中分布在小径阶，但较大径阶仍有林木分布，只是株数很少。从林木株数分布看，人工针叶同龄混交林林木株数分布与人工同龄纯林林木株数分布类似，小径阶林木株数在整个林分内所占比重最大。巴山林场人工针叶同龄混交林都处于中林龄阶段，中间径阶的林木株数在整个林分内最多。综上所述，在调查的10块标准地内，林木株数分布不尽合理，小径阶和被压木数量所占比重较大，这与森林缺乏适当的抚育措施有关，因此在未来的森林经营中，应采用合适的森林抚育措施，合理调整林分密度。

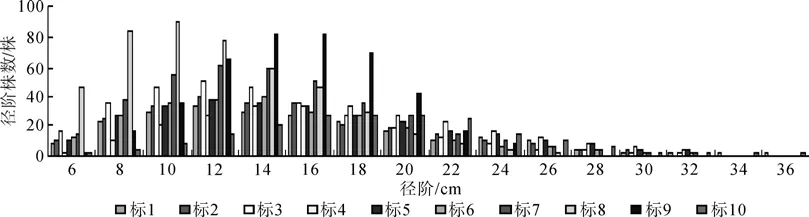
图1 各标准地林木各径阶株数分布Fig. 1 Tree number distribution of diameter class of standard plots

3.2 林分直径分布拟合与检验

3.2.1 参数估计及检验

研究直径分布时一般将Weibull分布函数和伽玛分布函数中参数a定为林分直径最小径阶的下限值，对于其它参数的求解用最大似然法求解[10-13]。参数检验采用卡方（λ2）检验。

各分布函数参数估计及其检验结果见表1。由表1可知，从λ2检验的结果来看，4种分布函数拟合直径分布的拟合效果依次为Weibull分布＞伽玛分布＞对数正态分布＞正态分布，说明Weibull分布可以很好地拟合人工针叶同龄混交林直径分布。从表1可以看出，Weibull分布函数形状参数c变化范围为1.685 2～2.284 8，说明分布函数形状为单峰山状曲线，这与实际中是相符的。分析计算所得的威布尔分布函数参数值，并结合标准地计算数据比较可知，标准地5每公顷株数接近8个标准地的平均值，每公顷蓄积量为8个标准地中最大。从表1可以看出，标准地5 Weibull分布函数参数c=1.8213，b=12.132 3，接近所有参数的平均水平；函数偏度值为0.569 3，亦接近分布函数偏度的平均值。通过以上分析可以得出一个参数确定的威布尔分布函数，运用这一分布函数去拟合其它标准地，考查这一参数是否适合于其它标准地。

3.2.2 Weibull分布函数拟合及其检验

用已经确定好参数的Weibull分布函数分别拟合8个标准地的直径分布，拟合结果见表2。

由表2可知，按照标准地计算的Weibull分布函数参数来拟合其它标准地，拟合精度平均为90%以上，卡方检验值都小于水平在0.05的卡方值，说明用标准地5得出的威布尔分布函数参数值能够很好地拟合其它标准地直径分布情况，拟合精度相对较高；标准差处于5.6至6.1之间，说明分布函数拟合的直径分布情况与实际直径分布情况接近，可以用来预测林分直径株数。

3.2.3 标准地林分株数预测

用得出的具体Weibull分布函数计算标准地9和10的林木株数，得出理论株数和实际株数分布的情况。从图2中可以看出，用Weibull分布函数拟合的标准地9和10林木理论株数与实际株数很接近，实际株数与理论株数相差不明显，说明对于人工针叶同龄混交林可以用尺度参数为12.132 3、形状参数为1.821 3的Weibull分布函数来预测林木株数，其预测精度高，实际森林经营中可以用来调整林木株数密度，为合理调整林分结构提供理论基础 。

表1 直径分布函数参数估计及检验值Table 1 Parameter estimation and test values of diameter distribution functions

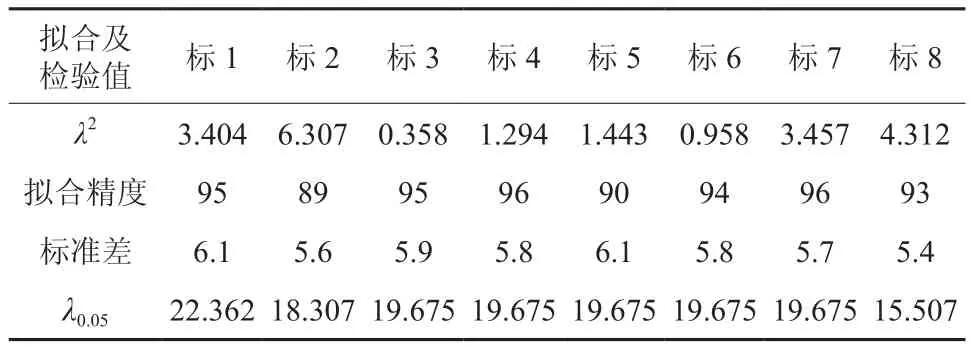
表2 威布尔分布拟合精度及其检验值Table 2 Fitting accuracy and test values of Weibull distribution

图2 标准地9和10实际株数与理论株数比较Fig.2 Comparison of actual and theory number of standard plot 9 and 10

综上所述，用尺度参数为12.132 3、形状参数为1.821 3的Weibull分布函数拟合人工针叶同龄混交林直径分布可以取得很好的结果，其混交林林木理论株数与实际株数很接近，可以用这一固定参数的威布尔分布函数来预测巴东针叶混交林林木株数及分布，为合理经营森林提供理论依据。

4 结 论

（1）巴山林场人工针叶同龄混交林直径分布服从Weibull分布。

（2）当Weibull分布函数参数尺度参数为12.132 3，形状参数为1.821 3时，可以运用这一固定参数值的Weibull分布函数预测针叶同龄混交林林木株数。

（3）通过对林分直径株数分布预测结果分析，证明了该函数的准确性和适用性，可以为当地森林经营时合理调整林分株数提供理论依据。

[1] 孟宪宇.测树学[M]．北京：中国林业出版社,1996:50-100．

[2] 马友平,冯仲科,刘永清.日本落叶松人工林直径分布规律的研究[J].林业资源管理,2006,5:40-42,70.

[3] 曾思齐,张 敏,肖化顺，等.青石冈林场木荷杉木混交林更新演替研究[J].中南林业科技大学学报,2013,33(1):1-6.

[4] 赵朝辉,方 晰，田大伦,等. 间伐对杉木林林下地被物生物量及土壤理化性质的影响[J].中南林业科技大学学报,2012,32(5): 102-107.

[5] 王春香,张秋良,春 兰，等.大青山落叶松人工林直径分布规律的研究[J].山东农业大学学报,2011, 42(3):349-355.

[6] 张惠光.杉木人工林直径分布模型[J].福建林学院学报,2004,24(4): 335-339.

[7] 孟宪宇.使用Weibull函数对树高分布和直径分布的研究[J].北京林业大学学报,1988,10(1):40-48.

[8] 吕 勇.树木树高曲线模型研究[J].中南林学院学报,1997,17(4):86-89.

[9] 王益和.马尾松人工林相对树高曲线模型及其应用研究[J].福建林业科技,2000,27(1):36-39.

[10] 龚直文,亢新刚,杨 华,等.长白山杨桦次生林直径结构研究[J].西北林学院学报,2009,24(3):1-6.

[11] 黄庆丰.马尾松林分直径结构规律的研究[J].安徽农业大学学报,1998,25(1):23-25.

[12] 惠刚盈,盛炜彤.林分直径结构模型的研究[J].林业科学研究,1995,8(2):127-131.

[13] 段爱国,张建国,童书振,等.杉木人工林林分直径结构动态变化及其密度效应的研究[J].林业科学研究, 2004,17(2):178-184.

Fitting of diameter distribution of even-aged mixed conifers plantation in Badong County

ZHANG Feng, SHI Jun-nan, ZHANG Dan-hua, WU Jiang
(Central South University of Forestry & Technology, Changsha 410004, Hunan, China)

Based on the standard survey data of even-aged artificial needle mixed forests in Badong County, and by adopting three parameters Weibull distribution function, normal distribution function, gamma distribution function and the logarithmic normal distribution function, the plantation’s diameter distribution were fitted. By combining with 2 testing method, the function that can accurately describe the artificial coniferous plantation diameter distribution law and its parameters were set up, and then through the established distribution function, the stand’s diameter class and plant number distribution can be predicted and analyzed. The results show that of the four distribution functions fitting stand diameter distribution, Weibull distribution is obviously significantly better than the remaining 3 kinds of distribution functions, the Weibull distribution had best fitting effect and high precision, and can describe the even-aged needle mixed diameter distribution very good. Given Weibull distribution function parameters a = 5.0, b = 12.132 3, c =1.821 3, the tree number of the plantation can accurately predicted, and the prediction results showed that the function’s accuracy and suitability were very good. The adjustments of stand’s plant number distribution by using the Weibull distribution function have some reference values in improve the quality of forest stands and enhance forest land productivity.

coniferous mixed forest; even-aged mixed conifers plantation; distribution function; diameter distribution; fitting effect

S758.5+5

A

1673-923X(2013)09-0038-04

2013-02-10

林业公益性行业科研专项“林业资源多层次信息服务技术研究” （201304215）

张 峰（1987-），男，甘肃天水人，硕士研究生，主要从事森林可持续经营及林分生长模拟研究；

E-mail：893112258@foxmail.com

石军南（1957-），男，湖南长沙人，教授，博士，硕士生导师，主要从事森林资源监测及数字林业教学与科研工作；E-mail：junnan000@163.com

[本文编校：谢荣秀]