游客教育人群生态动力学模型
2013-12-28文首文魏东平
文首文,徐 勇 ,魏东平
(1.深圳职业技术学院 管理学院,广东 深圳 518055;2.中南大学 数学科学与计算技术学院,湖南 长沙410075;3.上海大学 管理学院,上海200444)
游客教育人群生态动力学模型
文首文1,徐 勇2,魏东平3
(1.深圳职业技术学院 管理学院,广东 深圳 518055;2.中南大学 数学科学与计算技术学院,湖南 长沙410075;3.上海大学 管理学院,上海200444)
假设旅游地各类利益相关者的内禀增长率α受到游客教育活动的随机干扰,参照Logistic模型,构建了游客教育活动持续作用下多利益相关者的增长模型,获得了在游客教育这种外力干预影响下,旅游地人类生态系统存在性以及可持续发展的条件。其主要步骤和方法是:先把游客教育归化为一个数学上反映其基本现象的微分动力模型,然后用数学的解析方法得到足够精度的近似解,再以求得的结果为依据,从生态学、社会学、教育学、数学、物理学等多角度来分析其动态规律。分析发现,旅游地利益相关者内禀增长率随机化后,随机项能压制解的增长,且内禀增长率的确定项系数和随机项系数满足一定条件后,旅游地人类生态系统会得以安全发展,所以运用游客教育干预手段来调节旅游地利益相关者内禀增长率,从而促进旅游地社会生态系统和自然生态系统的和谐稳定是可行的。
游客教育;干预;随机项;内禀增长;旅游生态系统;人群生态动力学
现代人类生态系统是由人口、生产、消费、资源、环境所构成的多要素复合系统[1],人在这个系统中表现为一种群体结构[2],既是生产者,又是消费者;既是经济主体,又是生态主体。1798 年,英国科学家T.R.Malthus提出用一个指数增长模型来描述人类这个特殊的种群动力系统,并对1700~1961年的世界人口数目进行了较好地拟合[3]。1838 年,荷兰生物学家P.F.Verhulst对Malthus模型进行了改进,提出了生态学领域熟知的Logistic人口增长模型,但由于没有很好地考虑到资源及空间的局限、生产力与文化水平以及传统观念等因素,200多年来,许多学者不断对Logistic模型进行了修正[4-5],并广泛应用于自然生态系统和社会生态系统的种群预测与动力学机制研究中[6-7]。
游客教育是旅游地人类生态学研究的一个新兴方向。自20世纪60年代开始,一些国家和地区采用生态系统理论分析和解决旅游所带来的生态安全问题[8],并通过教育干预的手段对游客行为进行隐性管理(如美国实施的“不留痕迹教育项目”)[9]。许多实验证明[10-11],通过游客教育这种行为调节,可以规范游客的生态意识和行为,促进旅游资源供应在旅游生态系统内部得到合理分配,甚至把个别个体从群体中排挤出去(比如,美国阿拉斯加德纳里国家公园对进入偏远地区开展徒步旅行和野营项目的游客进行入园考试,只有全部回答正确才会获得入园许可;在世界遗产厄瓜多尔加拉帕哥斯群岛,如果游客不按规定行事,导游有权在剩余的行程中将游客限制在所乘游艇上),最终基于统一的价值观形成一致的行为规范,共同参与生态保护,使利益相关者密度控制在合理范围内,达到维持生态系统平衡的目的。由于游客教育活动涉及“自然—社会—经济复合生态系统”的复杂性和非线性动力学模拟与预测问题,目前国内外很少开展与之相关的生态动力学机制研究,因此,本文亦属于国际资源-生态领域刚刚起步的有关生态复杂性预测的前沿问题。
1 模型构建
假设在旅游产业生态系统中有n类利益相关者,在不考虑利益相关者的迁移时,参照Logistic模型,可将其增长模式写为:

式中,N代表利益相关者的产出水平,r是产出增长率,t代表时间,e为利益相关者消亡(倒闭)率,K为所有利益相关者在旅游地自然环境资源条件允许下产出增长达到的最大值;(K-N)/K代表环境阻力。它是理想环境和实际条件下旅游产出增长率之差,也就是妨碍利益相关者旅游生产能力实现的环境限制因子的总和。
考虑利益相关者的迁移后,用c表示迁移繁殖率,将(1)式的两边同除以K,并用p=N/K表示某时刻利益相关者对旅游生产总值的贡献度,则(1)式可改写为:

由式(2)可以看出,方程右边不显含时间变量,属于自治动力系统。由于游客教育活动是持续作用于旅游自然环境与所有利益相关者的,对旅游产业生态系统的影响是持续的,客观上存在着不同尺度的周期性,所以,游客教育活动效应该是时间的函数。设游客教育活动对旅游产业生态系统的影响效为D(t),那么在游客教育活动效应的影响下,旅游产业生态系统的剩余容纳量为(1-D(t)),这样就可以将游客教育活动效应下不显含时间的自治动力模型扩展为非自治的多时间尺度的动态模式:

式(3)里的D随着时间的推移而发生动态的变化,在不同的时段具有不同的值,既可以是时间的线性函数,也可以是各种周期和非线性函数。其表示如下:

式中,a代表游客教育的强度,a越大,游客教育活动效应越大;T表示游客教育周期性活动的周期,即不同的时间尺度。这样(3)可以改写为:游客教育活动效应下的单类利益相关者的增长模型:
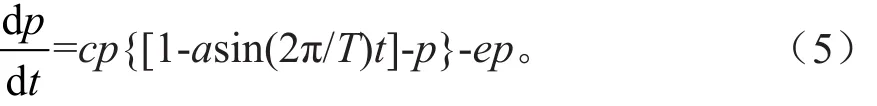
游客教育的目的就是通过改变或影响游客的知识和态度,规范和引导旅游地其他利益相关者的行为,促进旅游地人类生态系统的平衡。但游客教育是一个复杂的非线性动力学过程,游客教育系统分析更是一个重要而困难的理论课题。相比一般的随机动力系统,游客教育系统中的随机性可能来自初始条件的不确定性,也可能包括外部激励和系统参数的变异性。由于游客教育过程中出现的各种随机性,系统的响应和性态将是随机变量、随机过程或随机场,因而,要从样本轨道的角度对系统进行精确的把握,往往是困难甚至是不可能的[12]。所以,方程(5)里用一个常数α来描述游客教育强度就过于简单,本文假设α受到随机干扰,于是有其中,wt为Brown运动。于是方程(5)可转化为随机微分方程:


2 模型分析
易知方程的平衡点为X= Kα, 旅游地人群生态系统的可持续发展研究是一个非常重要的研究,下面我们将从随机动力学机制分析旅游地人群生态系统可持续发展系统存在及其条件。通过研究,我们发现对于非随机系统可能存在爆破的状态,但加入游客教育干预的随机项后,只要随机项前的系数满足很简单的条件就能抑制解的爆破,使得旅游地人群生态系统能可持续的发展。首先我们将证明随机旅游地人群生态系统可持续发展系统存在性,即方程(6)的正整体解的存在唯一性。
定理1:定理1:若β≠0,则方程(6)存在唯一正整体解.
证明:因为方程(6)的系数满足局部Lipschitz条件,对任意初始值p0∈R+,则存在唯一局部解 p(t),t∈ [0,τe],其中 τe是解的爆破点。为了证明这个解p(t),t∈[0,τe]是全局的,只需证明τe=∞ a.s.。设正整数k0>0充分大,使得初始值对任意正整数k≥k0,定义停时
τk=inf{t∈ [0,τe): p ( t ) ∉ ( 1/k,k)},
其中,假设infΦ=∞,Φ代表空集。显然τk是随 着k递 增的。设,则 τ∞≤ τe, a.s.。如果能证明 τ∞=∞, a.s.,则 τe=∞, a.s.,即对任意t≥0都有p(t)>0。为了证明这个结论,我们定义一个C2函数V∶R+→R+
V(x)=x-1-0.5log x
显见上述V函数是非负的:即x-1-0.5log x≥ 0,x> 0。由 Itoˆ公式可知:


因此

显见上式只要β≠0是上有界的,不妨记其上界为K>0,因此我们有

对上式左右两边取期望可得
EV[p(t)] ≤ EV(p0)+Kt=Kt。
让 t=τk∧ T,可得 EV[p(τk∧ T)]≤ KT由 τk的定义可知,p(τ)=k或者,所以有
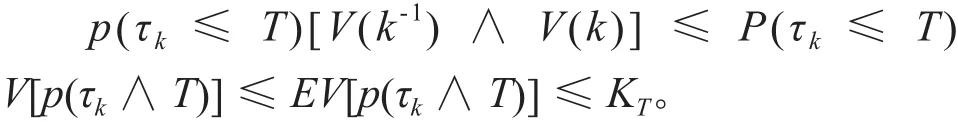
定理1说明在旅游地人群生态系统可持续发展系统中,游客教育干预随机项起着决定性作用,它完全能控制系统解的存在唯一性。讨论了随机旅游地人群生态系统可持续发展系统解的存在唯一性后,接下来研究系统的可持续发展条件,即方程(6)正整体解持久性条件,这意味着方程(6)能持续发展下去。首先给出方程(6)解的持久性定义。
定义1:对于任意初始值X0>0,如果方程(6)的解X(t;X0)都满足如下性质

则称方程(6)的解X(t;X0)以概率1具有持久性。
定理2:若方程(6)的系数满足如下两个不等式
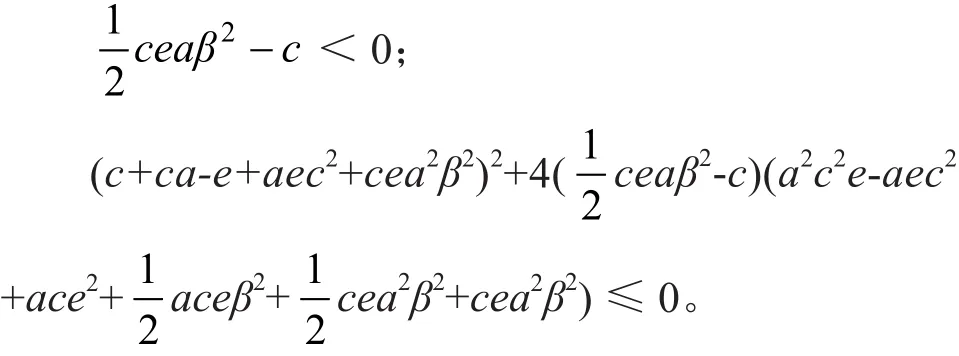
则方程(6)的解p(t;p0)以概率1具有持久性。并且对任意初值p0>0,方程(6)的解p(t;p0)都满足如下性质

证明:定义一个C2函数V(x)=ace[(x/ace)-1-log(x/ace)],容易知道函数V(x)具有非负性。根据Ito公式可知

因此可以得到
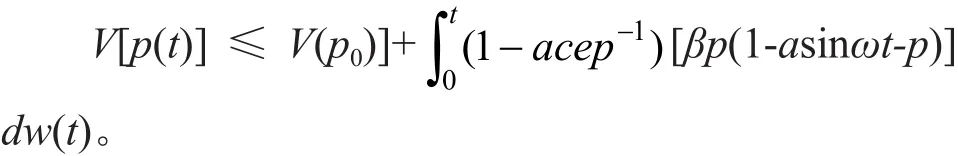
由于V[p(t)]的非负性

由非负半鞅收敛定理知

因此,必有

从定理2可以看出方程(6)在一定条件下,对任意初值,解p(t;p0)会一个区间内持续运行下去,这意味着旅游地人群生态系统在一定条件下是可持续增长的。
3 结 论
(1)研究表明,游客对生态系统的认知直接影响其旅游行为是否“绿色”、环保,而人们往往习惯用自己已经具有的图式去认知事物,如果一个事物不能纳入已有的图式,这就要调整改造已有的图式,即必须进行干预和调节。本研究试图通过随机动力学模型解释游客教育随机项对利益相关者可持续增长的干预与调节作用,分析结果发现,旅游地利益相关者内禀增长率随机化后,随机项能压制解的增长,且内禀增长率的确定项系数和随机项系数满足一定条件后,旅游地人类生态系统会得以安全发展,所以运用游客教育干预手段来调节旅游地人群生态系统内禀增长率,从而促进旅游地社会生态系统和自然生态系统的和谐稳定是可行的。
(2)从生态学的观点来说,游客教育是一个相当复杂的现象,本文设计的随机干扰项就是一个研究这种复杂现象的简单、有效的路径。它的主要方法是:先把游客教育归化为一个数学上反映其基本现象的微分方程模型,然后用数学的解析方法得到足够精度的近似解,再以求得的结果为依据,从生态学、社会学、教育学、数学、物理学等多角度来分析其动态规律。
(3)从数学理论观点来看,尽管微分方程(1)的解是不可持续的,本文通过增加适当的随机项,控制了确定性方程解在有限时间的爆破,从而证明了随机微分方程(6)(即游客教育活动持续作用下的人群生态动力学模型)解的存在性和持有性。这也反映出随机项在人们印象中并不都是起“坏”的干扰作用,正如本研究中的随机项在整个方程中就是正面的因素,保证了系统解的存在性和持久性。这无疑从理论上证明了游客教育随机项在人群生态动力学中的控制作用。另外,要进一步得到方程的解,还可以采用数值方法模拟方程的近似解,而这种近似解求解方法目前已有广泛应用[13]。
[1] 文启胜.人类生态系统中的资源、环境转化机制[J].生态经济,1990,6(5):3-6.
[2] 南忠仁,赵传燕.人类生态系统组成、结构与功能研究[J].西北师范大学学报:自然科学版,1991,27(3):75-80.
[3] 江 南.基于浙江省的人口模型的研究[D].杭州:浙江大学,2006:1-5.
[4] 孙仁斌,胡军浩.受扩散与时滞及食物限制影响的人口模型[J].数学的实践与认识,2006,36(5):137-141.
[5] 王文娟,冯晓梅,龚固斌. 单种群时滞反馈控制生态系统的全局稳定性[J].中南林业科技大学学报,2011,31(4):210-213.
[6] 李晓月,范 猛,王 克.具反馈控制和无穷时滞单种群模型周期正解[J].高校应用数学学报(A辑),2002,17(1):13-21.
[7] Keitt T H, Lewis M A, Holt R D. Allee effect, Invasion Pinning, and species’ borders[J].The American Naturalist.2001,157(2):203-216.
[8] 王 辉,姜 斌.沿海城市生态环境与旅游经济协调发展定量研究[J].干旱区资源与环境,2006,20(5): 115-119.
[9] 文首文,徐洁华.游客教育的概念、体系与意义刍议[J].中南林业科技大学学报:社会科学版,2009,3(1):93-95.
[10] Hart Paul. New backcountry ethic: Leave no trace[J]. American Forest,1980,86(8):51-54.
[11] 文首文,吴章文.生态教育对游憩冲击的影响[J].生态学报,2009,29(2):768-775.
[12] Mao X R. Stochastic differential equations and applications[M].West Sussex:Horwood Publishing Limited,2007:62-135.
[13] Mao X R. Exponential Stability of Stochastic Differential Equations[M]. New York: Marcel Dekker,1994:28-89.
Biological dynamic model for tourist education human groups
WEN Shou-wen1, XU Yong2, WEI Dong-ping3
(1.Department of Management, Shenzhen Polytechnic, Shenzhen 518055, Guangdong, China; 2.School of Mathematical Sciences and Computing Technology, Central South University, Changsha 410075, Hunan, China; 3.School of Management, Shanghai University,Shanghai 200444, China)
The increase model of multi-stakeholders that the tourist education activity acts uninterruptedly on, were set up by consulting Logistic model, base of the hypothesis that the intrinsic rate of increase (α) of multi-stakeholders in the sightseeing district affected the random disturbance of the tourist education activity. The existence of the sightseeing district and conditions for sustainable development were studied with the outside interference of tourist education. The modeling method and procedures were as followings: firstly, the tourist education activity was naturalized as a differential dynamic model which can reflect the basic phenomena of the sightseeing district; then through mathematical analysis method, the approximate solutions with sufficient accuracy were obtained; finally according to the solutions, from the multi-angles of ecology, sociology, pedagogics, mathematics, physics etc., the dynamic laws of tourist education Groups of the sightseeing district were analyzed. The analysis results show that after the intrinsic rate of increase (α) of multistakeholders in the sightseeing district was randomized, the random entry could suppressed the increase of the solutions, and after the intrinsic increase rate’s uncertain term coefficients and random term coefficients had been satisfied the controlled conditions, the human ecology system in the tourism destination could safely develop. So, it is feasible that using tourist education interventions regulate the intrinsic rate of increase (α) of multi-stakeholders in the sightseeing district, and further promote social harmonious stability in ecological systems and natural ecosystems in the sightseeing district.
tourist education; educational intervention; stochastic component; intrinsic rate of increase; ecological tourism system;Biological dynamic model of human groups
S788.2
A
1673-923X(2013)09-0126-05
2013-02-01
国家社会科学基金项目(11BGL053);国家自然科学基金项目(11101434)
文首文(1976- ),男,湖南沅江人,副研究员,博士,研究方向为生态旅游与生态教育;E-mail:82104829@163.com
[本文编校:吴 毅]
