降雨再分配的回归模型差异性分析——以黄土高原半干旱区油松人工林为例

赵明扬，孙长忠，康 磊

（中国林业科学研究院 华北林业实验中心，北京 102300）

降雨再分配的回归模型差异性分析
——以黄土高原半干旱区油松人工林为例

赵明扬，孙长忠，康 磊

（中国林业科学研究院 华北林业实验中心，北京 102300）

根据2008年6月至2011年11月黄土高原半干旱区油松人工林林内降雨定位观测数据，就该地区油松林内降雨再分配规律进行研究，并对不同立地条件下回归模型的结果进行分析。结果表明：穿透雨量、树干茎流量、林冠截留量与降水量均呈极显著的线性关系（P＜0.01），穿透雨率和树干茎流率与降雨的关系可用非线性曲线表示；林冠截留率随降雨量的增加呈双曲线下降，林冠截留率受降雨量、降雨持续时间等因子的影响；从拟合回归的参数值来看，不同年份、不同林冠下的降雨特征存在差异，回归模型参数呈现不稳定性。

油松人工林；差异性分析；降雨再分配；穿透雨；树干茎流；林冠截留

在黄土高原半干旱区，水分是林分生产力及稳定性的限制因子，而降雨几乎是林地水分的唯一来源。林冠对降雨的再分配作用直接影响着林分涵蓄降水能力的大小和产生地表径流的能力，是森林生态效益研究的重要内容之一[1-6]。降雨发生后首先在植物的表面产生第一次分配并产生相应的林冠截留[7]，通过植被层的作用，降雨被重新分配为穿透雨、树干茎流和林冠截留。目前国内外对降雨再分配的规律均做了大量研究[8-12]，如在国外对奥克兰3种林地的林冠截留进行了研究[13]，李淑春等[14]对冀北山地不同林分类型林冠层的降雨再分配进行了研究，陈书军等[15]对秦岭天然次生油松林的林冠层降雨再分配进行了研究，在黄土高原这一降雨稀少的特殊区域，更有其特殊的意义。本研究通过对林内降雨再分配回归结果的对比分析，研究其再分配规律，旨在揭示不同条件下降雨再分配的差异性，为森林水文效应研究提供理论参考。

1 研究地区概况与研究方法

1.1 自然概况

试验于2008年6月起在山西省偏关县陈家营观测站进行。该研究区地处晋西北的晋蒙交界处， 位 于 东 经 111°22′～ 11°01′、 北 纬 39°12′～39°40′之间，海拔1 377 m，大陆性气候，年平均气温3～8 ℃，年平均降水量为425.3 mm，7～9月份的降雨占全年的60%以上，植被以人工乔木林和灌丛为主，主要造林树种有：油松Pinus tabulaeformis、侧柏Patycladus rientalis和樟子松Pinus sylvestnis var. monglica Litv.等。土壤为沙质黄绵土，供观测的人工油松纯林为28年生，平均树高4.3～5.2 m，平均胸径9.4～11.9 cm，郁闭度 0.67～ 0.85。

1.2 研究方法

采用设置长期固定标准地的方式进行林地内外气象因子的定位观测，采用回归分析方法进行观测数据的分析。

1.2.1 样地的设置

在具有代表性的油松林内设置3个固定样地，具体规格见表1。在林外附近空旷地设置气象站一个。

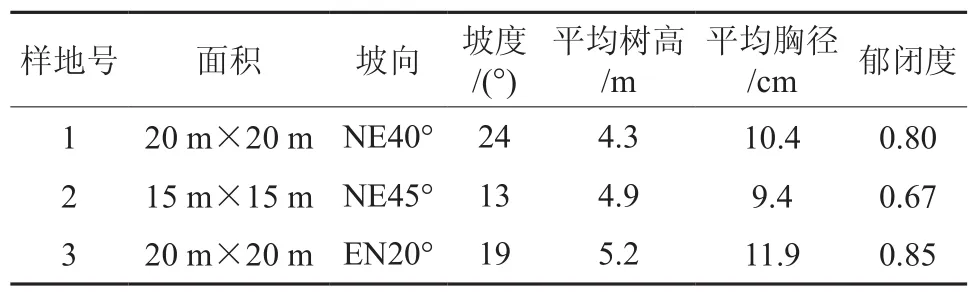
表1 油松试验林基本情况（2008年）Table 1 Fundamental circumstances of P. tabuliformis experimental forest

1.2.2 林外降雨及气象因子的测定

在林外设置的气象站内安置百叶箱、雨量筒及蒸发皿等气象仪器，每日的8:00、14:00和20:00进行以下主要指标的观测：降水量(mm)、气温(ºC)、空气相对湿度(%)和风速(m·s-1)等。

1.2.3 林冠截留量的测定

林冠截留的降雨主要消耗于蒸发，减少了地面的实际雨量和林地土壤水分的有效补充，是雨水资源的无效消耗。林冠截留包括树叶、树枝及树干截留的降雨，其计算公式为：

I=P-（TF+SF）。

式中：I为林冠截留量(mm)； P为降水量(mm)，即林外降雨量；TF和SF分别为林内穿透雨量(mm)和树干茎流量(mm)。

1.2.4 林内穿透雨的测定

林内穿透雨是直接穿过林冠到达林地的那部分降雨。在每个实验样地随机布设7个雨量筒，每次降雨后测定其穿透雨量（mm），取其平均值作为林内穿透雨量（TF），并计算穿透雨率(TR)，公式如下：

TF=TF/P×100%。

1.2.5 树干茎流的测定

在每个样地（经抚育的人工同龄林，林相整齐，单株差异较小）内选择具有代表性的3株标准木，在距离树干基部1.3 m处，将直径10 cm的聚乙烯塑料管刨开后围绕树干2周，铁钉固定，用玻璃胶将塑料软管与树干的接缝处封严，在软管下端用塑料桶接水，每次降雨后用量筒量测桶内的水量(mL)，并将其换算为树干茎流量（mm）。具体的林地树干径流量（SF）计算公式如下：

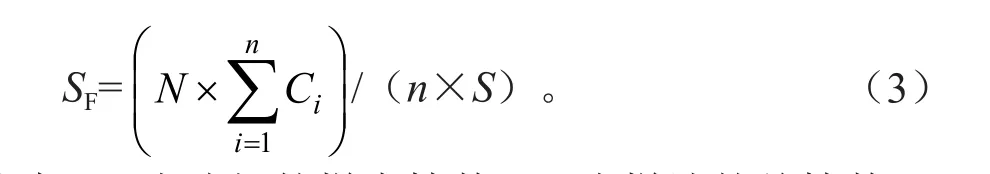
式中：n为选择的样木株数；N为样地的总株数；Ci为第i个样木的树干茎流体积；S为样地的面积。

树干径流率(SR)的计算公式如下：

SR=SF/P×100%。 （4）

1.3 数据处理

采用开源软件R2.15.1对数据进行处理和分析[16]。

2 结果与分析

2.1 林外降雨量的特征分析

根据2008年6月至2011年11月的观测资料，最大值通常出现在8～9月份，最大月降雨量可达到156.87 mm，次降雨量的最大值为64.7 mm，最小值为0.7 mm，平均次降雨量为12.0 mm。

2.2 穿透雨与降雨量的关系

研究期间，2008年到达样地内的穿透雨总量为：样地（1） 370.6 mm，样地（2） 350.5 mm，样地（3） 329.1 mm，分别占同期林外降雨量的76.39%、71.91%和62.74%；2009年3个样地分别为319.9、322.1和319.9 mm，分别占同期林外降雨量的70.64%、71.29%和70.64%；2010年为352.1、343.0和344.7 mm，分别占同期林外降雨量的75.80%、76.91%和74.97%；2011年为233.5、233.0和232.1 mm，分别占同期林外降雨量的72.88%、73.02%和72.11%。

根据观测数据就穿透雨—林外降雨与穿透雨率—林外降雨关系作图（以2008年1号样地数据为例），结果见图1。从图1中可以看出，穿透雨量与林外降雨量之间的线性关系明显，可用方程（5）进行拟合研究。

TF=aP-b。 （5）

穿透雨率与林外降雨呈曲线关系，可用方程

（6）进行拟合研究。

TR=a+bP/(c+P)。 （6）

经用其它年份和样地的数据进行相应的分析验证，其结果与其近似，故选取上述2个拟合方程进行回归分析。

根据研究期内不同年份观测数据对上述2个拟合方程进行回归分析，结果见表2。

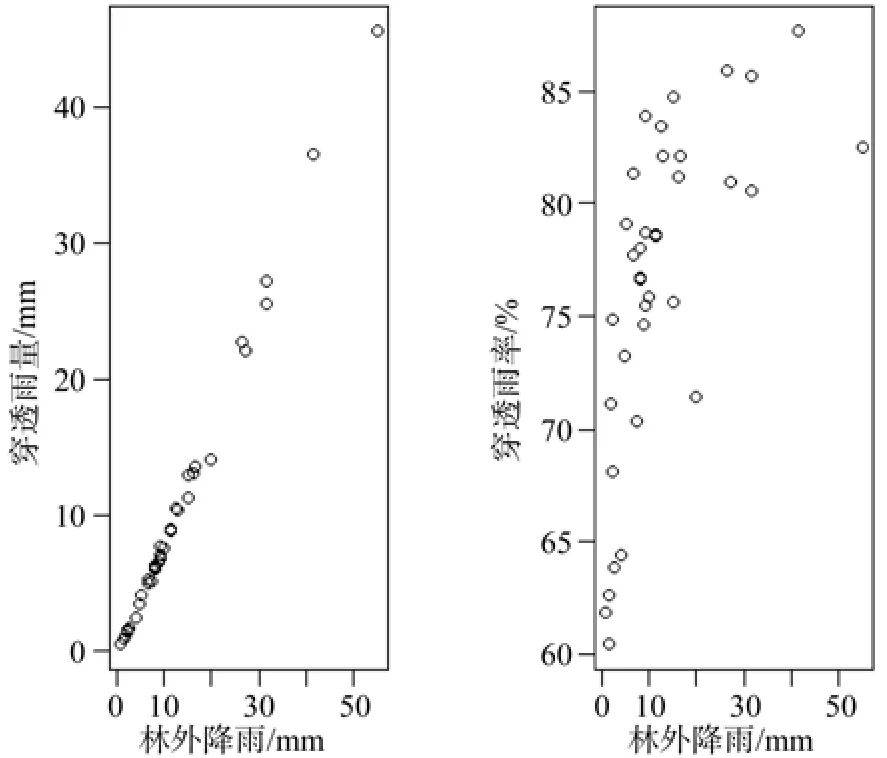
图1 穿透雨量-林外降雨量与穿透雨率-林外降雨量关系Fig.1 Relation between through-fall and rainfall and relation between through-fall ratio and rainfall

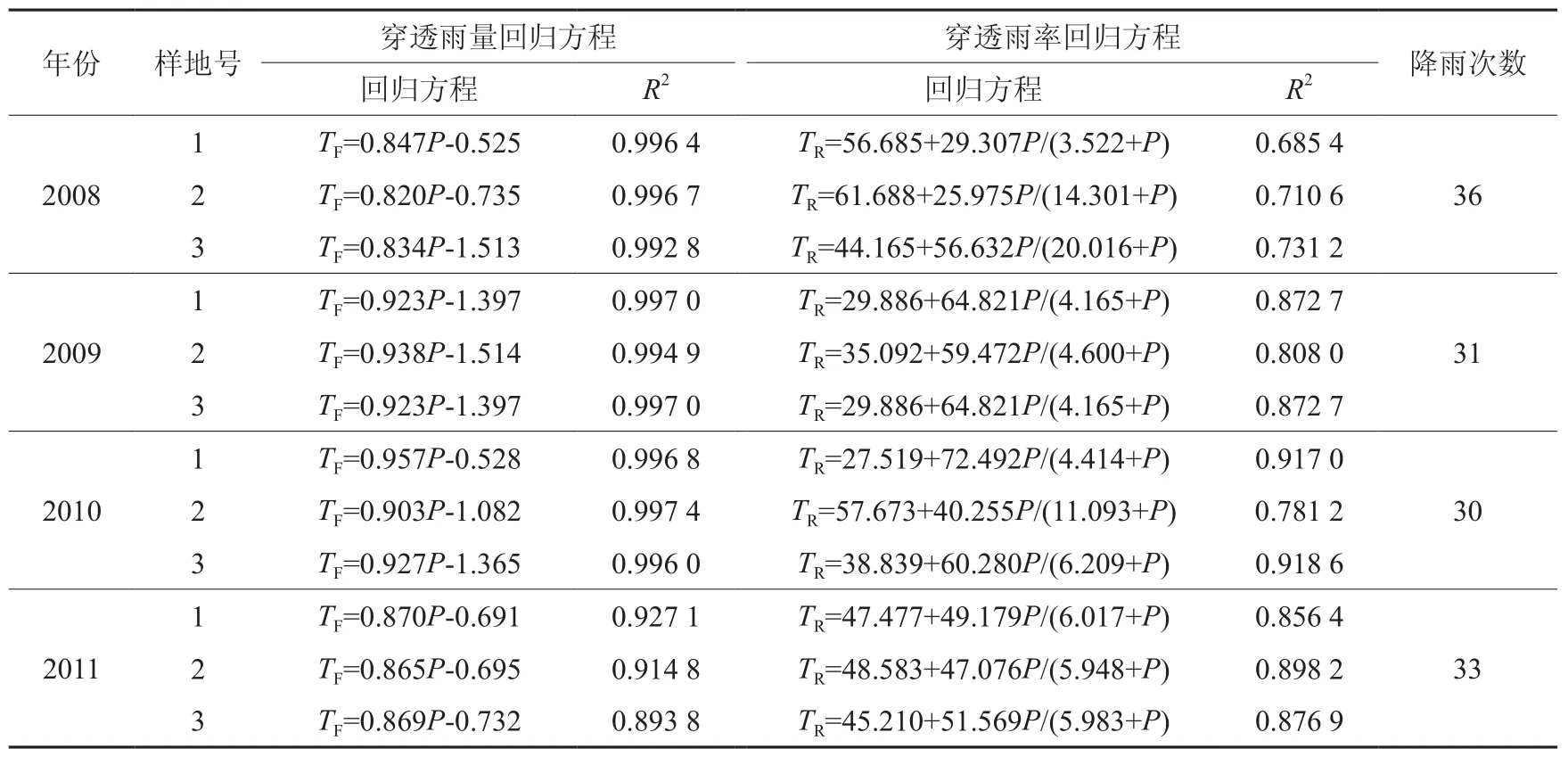
表2 2008～2011年3个样地的穿透雨回归模型Table 2 Regression models of through-fall about 3 test plots from 2008 to 2011

由表2可知，研究区林内穿透雨量随降雨量的增加而增加，两者的线性关系极显著（P＜0.01）。而林内穿透雨率的变化幅度较大，在一定降雨量范围内随着降雨量的增加，穿透雨率先急剧增加，而后随着降雨量的增加，穿透雨率变化幅度不大。从同一年份的不同样地来看，系数之间的变动幅度较大，如2010年拟合系数a值的变动幅度从27.519到57.673，b值的变动幅度从40.255到72.492，c值的变动幅度为4.165到11.093，其它年份不同样地之间也表现出了类似的系数不稳定性。而从同一样地的不同年份来看，其变动幅度较大，如1号样地的回归系数中，a值的变动幅度为29.886到56.685，b值的变动幅度为29.307到72.492，c值的变动幅度为3.522到6.017，其它样地尽管变动幅度相对较小，但均表现出了不稳定性。

2.3 树干茎流与降水量的关系

树干径流量是降雨在林内再分配的重要分量，也是林地水量平衡研究不可忽视的重要内容。研究期间，2008年3个样地树干茎流总量分别为：样地（1） 6.0 mm，样地（2） 6.6 mm，样地（3）8.1 mm，分别占同期林外降雨量的0.83%、0.95%和1.17%；2009年分别为9.6、8.4 和7.2 mm ，分别占同期林外降雨量的1.79%、1.40%和1.17%；2010年分别为11.4、8.4 和11.4 mm ，分别占同期林外降雨量的1.82%、1.44%和1.70%；2011年分别为5.8、6.7 和6.8 mm ，分别占同期林外降雨量的1.43%、1.60%和1.77%。

利用2008年1号样地的观测数据绘制树干茎流量—林外降雨与树干茎流率—林外降雨关系直观图（见图2）。从图2可见，树干茎流与林外降雨的关系与穿透雨呈现出相似的规律，所以仍采用回归方程（5）和（6）对其进行回归分析，回归分析结果见表3。

图2 树干茎流量-林外降雨量与树干茎流率-林外降雨量关系Fig.2 Relation between stem-fall and rainfall and relation between stem-fall ratio and rainfall

从表3可见，树干茎流量和降雨之间呈极显著的线性关系（P＜0.01），而树干茎流率与降雨量的关系同穿透雨率表现出一样的规律[9-10]。从同一年份不同样地的树干茎流率的拟合参数来看，参数估计值之间存在较大差异，如2010年的估计参数b的变动范围为3.016到18.492，参数c的变动范围为15.276到105.404。从同一样地的不同年份来看，也呈现出不稳定性，如3号样地中参数c的变动幅度从8.287到105.404。

2.4 林冠截留与降水量的关系

研究期间，2008年3个样地林冠截留总量分别为：样地（1） 83.39 mm，样地（2） 102.9 mm，样地（3）122.7 mm，分别占同期林外降雨量的22.78%、27.15%和36.09%；2009年分别为55.2、63.0和66.4 mm，分别占同期林外降雨量的19.07%、27.32%和28.20%；2010年分别为52.2、64.3和63.2 mm，分别占同期林外降雨量的22.36%、21.65%和23.26%；2011年分别为55.4、54.9和55.67 mm，分别占同期林外降雨量的25.69%、25.34%和26.12%。

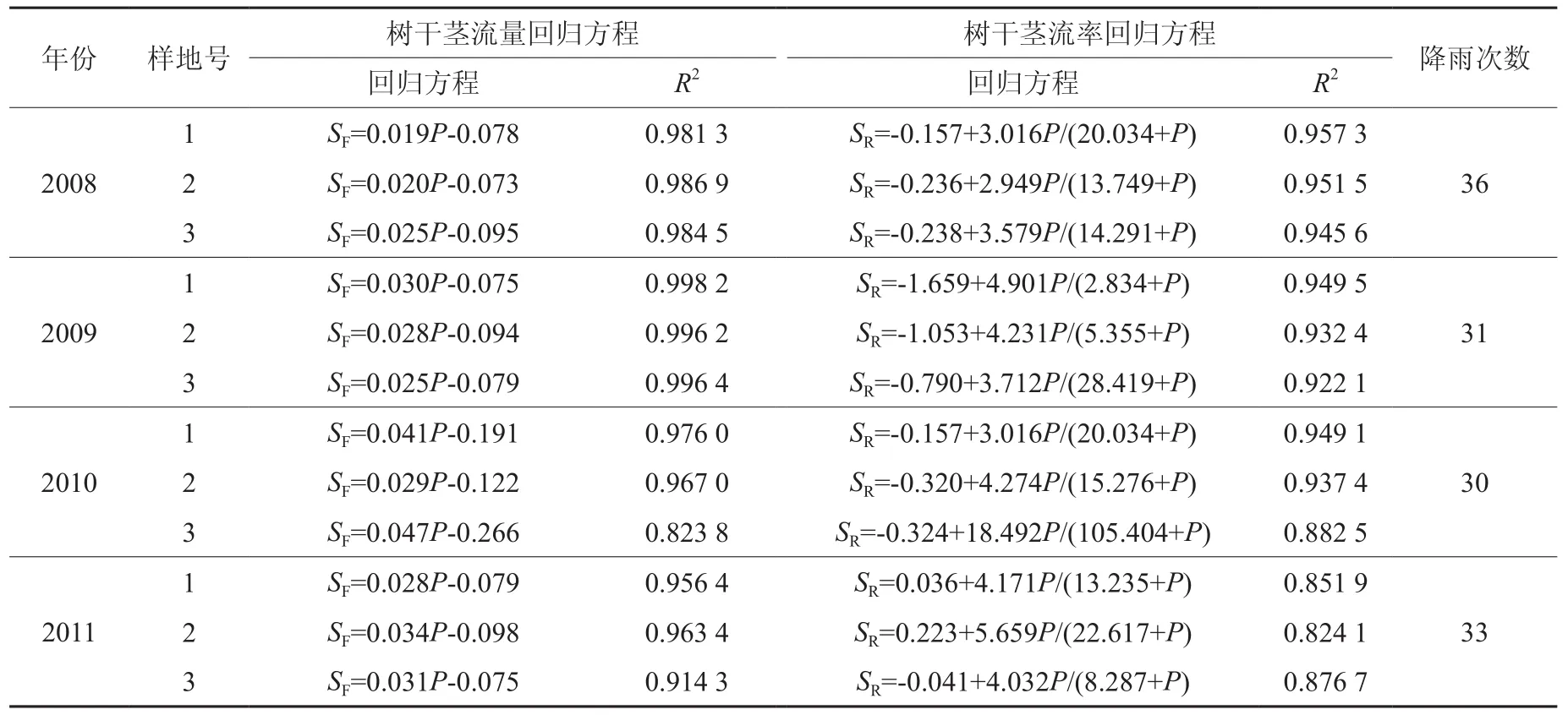
表3 2008～2011年3个样地的树干茎流回归模型Table 3 Regression models of stem-fall about 3 test plots from 2008 to 2011

利用2008年1号样地的数据绘制林冠截留量—林外降雨量与林冠截留率—林外降雨关系直观图（见图3）。

由图3可见，林冠截留量与林外降雨间的线性关系明显，故选取式（5）作为回归分析方程。而林冠截留率与林外降雨量之间的关系与曲线的变动趋势比较一致，故选取式（7）作为拟合方程。

IR=a+b/(c+P)。 （7）

根据4年3个样地观测数据进行回归分析，其结果见表4。

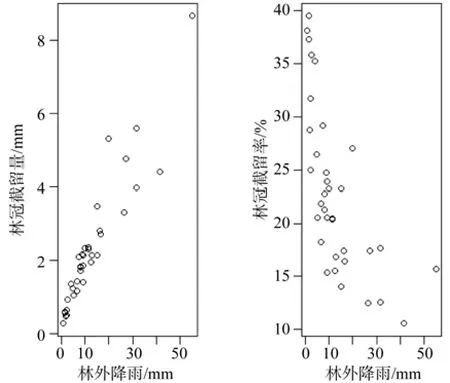
图3 林冠截留量-林外降雨量与林冠截留率-林外降雨量关系Fig. 3 Relation between canopy interception and rainfall and relation between canopy interception and rainfall

表4 2008年-2011年3个样地的林冠截留回归模型Table 4 Regression models of canopy interception about 3 test plots from 2008 to 2011

从表4各回归方程可知，研究区林内林冠截留量随降雨量的增加而增加，各实验样地均呈现显著的线性关系（P＜0.01）。林冠截留率的大小随着降雨的增加而呈双曲线下降，并最终趋向平稳，而且从不同的年份以及不同的样地分析发现在参数估计值方面均呈现较大的差异，如2008年3块样地的系数中，参数b的变动幅度从129.466变化到1 176.200，对于3号样地在不同年份的估计参数看，参数b亦呈现出了较大的波动，如从294.762变动到1 176.200，而其它的估计参数其变动幅度相对较小。

在表4林冠截留率与林外降雨关系的分析结果中，各年份各样地的估计参数呈现出了较大的变化，这种现象可能与气象因子有关。为了验证各种气象因子对参数估计的影响，用林冠截留率与降雨特性、降雨时各气象因子数据进行偏相关分析，其结果如表5所示。

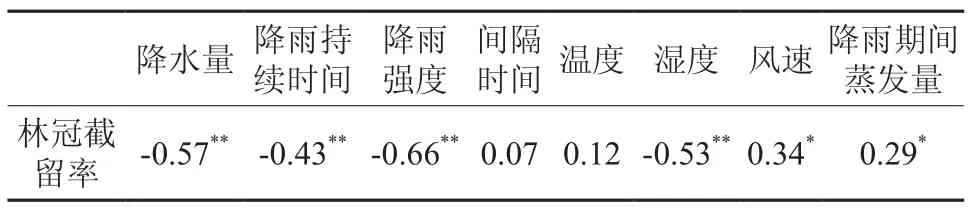
表5 林冠截留率与降雨特征及降雨时各气象因子的偏相关分析†Table 5 Partial correlation analysis between canopy interception ratio and rainfall characteristics with different climatic factors

从表5可以看出，降水量、降雨持续时间、降雨强度、湿度、风速和降雨期间蒸发量与林冠截留之间关系密切。单独考虑林冠截留率与降水量的关系，尽管在数据拟合上表现出较好的效果，但却会因为其它因子的影响对估计参数在时空上造成较大的波动，呈现出一定程度的不稳定性，从而导致回归模型的规律性不强。由于林冠截留量是根据式（1）计算获得，故这些因素也在一定程度上影响着穿透雨与树干茎流的估计。

3 结 论

（1）半干旱区人工油松林的林内穿透雨量、树干茎流量及林冠截留量随同期林外降雨量的增加而增加，二者的线性关系显著（P＜0.01），可用线性模型y=ax+b进行回归分析，且回归参数具有较好的稳定性。

（2）穿透雨率、树干茎流率与林外降雨量之间为非线性函数y=ax+bx/(c+x)关系，林冠截留率与林外降雨量为函数y=ax+b/(c+x)关系，但穿透雨率、树干茎流率和树冠截留率与林外降雨之间不同样地和不同年份的参数估计值均呈现出较大的差异而表现出不稳定性。

（3）半干旱区降雨总量小、多阵雨、气候干燥、空气湿度低的特殊气候特点与降雨特征，直接影响着林内降雨的再分配过程与规律。研究其森林水文作用规律，应充分考虑其气候特点和林分条件。同时，对林内降雨分配各分量进行定位测定时，应考虑观测仪器设备的安放数量与位置，尽可能减小观测误差，以提高估测模型精度与稳定性。

[1] 常志勇, 包维楷, 何丙辉, 等. 岷江上游油松与华山松人工林混交林对降雨的截留分配效应[J]. 水土保持学报, 2006,20(6):37-40.

[2] Gomez J A, Vanderlinden K, Giraldez J V, et a1. Rainfall concentration under olive trees[J]. Agricultural water Management, 2002, 55:53-70.

[3] Crockford R H, Richardson D P. Partitioning of rainfall into throughfall, stemflow and interception: effect of forest type,ground cover and climate[J]. Hydrological Processes, 2000,l4:2903-2920.

[4] 刘世荣, 温光远, 王 兵, 等. 中国森林生态系统水文生态功能规律[M]. 北京:中国林业出版社, 1996.

[5] 时忠杰, 王彦辉, 于澎涛, 等. 宁夏六盘山林区几种主要森林植被生态水文功能研究[J]. 水土保持学报, 2005, 19(3):134-138.

[6] 石培礼, 李文华. 森林植被变化对水文过程和径流的影响效应[J]. 自然资源学报, 2001, 16(5):481-487.

[7] 中野秀章. 森林水文学[M]. 北京:中国林业出版社, 1993.

[8] 何常清, 薛建辉, 吴永波, 等. 岷江上游亚高山川滇高山栎林的降雨再分配[J]. 应用生态学报, 2008, 19(9):1871-1876.

[9] Herbst M, Roberts J M, Rosier P T W. Measuring and modelling the rainfall interception loss by hedgerows in southern England[J].Agricultural and Forest Meteorology, 2006, 141:244-256.

[10] 苏开君, 王 光, 马红岩, 等. 流溪河小流域针阔混交林林冠降雨截留模型研究[J]. 中南林业科技大学学报, 2007, 27(1):60-65.

[11] 王珍珍, 文仕知, 杨丽丽. 长沙市郊枫香人工林降水再分配及养分动态[J]. 中南林业科技大学学报, 2008, 28(2):54-57.

[12] 吕 磊, 文仕知, 胡孔飞. 长沙市郊枫香人工林水文生态效应的研究[J]. 中南林业科技大学学报, 2010, 30(4):21-25.

[13] xiao Q F, McPherson E G. Rainfall interception of three trees in Oakland, California[J]. URBAN ECOSYSTEMS, 2011,14(4):755-769.

[14] 李淑春, 张 伟, 姚卫星. 冀北山地不同林分类型林冠层降水分配研究[J]. 水土保持研究, 2011, 18(5):124-127.

[15] 陈书军, 陈存根, 邹伯才, 等. 秦岭天然次生油松林冠层降雨再分配特征及延滞效应[J]. 生态学报, 2012, 32(4):1142-1150.

[16] 薛 毅, 陈立萍. 统计建模与R软件[M]. 北京：清华大学出版社, 2007.

Difference analysis of rainfall redistribution of Pinus tabulaeformis artif i cial forests in Loess Plateau

ZHAO Ming-yang, SUN Chang-zhong, KANG Lei
(Forestry Experiment Center of North China, Chinese Academy of Forestry, Beijing 102300, China)

Based on the observed data of rainfall in the Pinus tabulaeformis forests within the semi-arid areas of the Loess Plateau from June 2008 to November 2011, the rainfall redistribution lows were investigated and their results of regression models were analyzed under different conditions. The results show that the through-fall , stem-f l ow and canopy interception had signif i cant linear relationships with rainfall (P＜0.01), and the relationships of through-fall ratio and stem-f l ow ratio with rainfall could be described with non-linear curves. The canopy interception rate decreased hyperbolically with the increase of rainfall, being signif i cantly correlated with the rainfall amount, duration, and etc. By viewing from the fi tted regression parameter values, there were differences in rainfall characteristics under different years and different canopy, and the regression model parameters presented instability.

Pinus tabulaeformis artif i cial forests; difference analysis; rainfall redistribution; through-fall; stem-f l ow; canopy interception

S715.2；S791.254

A

1673-923X(2013)05-0079-06

2012-11-12

国家自然科学基金项目（30170769）：华林中心科学试验示范林功能恢复与提升研究(CAFYBB2012004)

赵明扬（1990-），男，河南漯河人，硕士研究生，研究方向：森林水文的数学模拟；E-mail: zmyedu@163.com

孙长忠（1957-），男，北京人，研究员，博士，研究方向：森林培育、森林生态等方面研究；E-mail: Sun61@163.com

[本文编校：谢荣秀]