竹环蜂窝托盘设计及理论研究

庞 燕，尹千才，曾 光

（中南林业科技大学 交通运输与物流学院，湖南 长沙 410004）

竹环蜂窝托盘设计及理论研究

庞 燕，尹千才，曾 光

（中南林业科技大学 交通运输与物流学院，湖南 长沙 410004）

竹环蜂窝板托盘是一种新兴的复合结构托盘，它把竹材的优势与蜂窝结构的优点完美地结合在一起，是一种很有应用潜力的托盘，但是关于竹环蜂窝托盘的设计理论研究还很少。运用夹层梁理论，结合实验对竹环蜂窝板的设计理论进行了研究，构建了关于蜂窝板承载力与结构尺寸关系的设计模型，为蜂窝板托盘实现产业化奠定理论基础。

竹环蜂窝板托盘；设计理论；力学性能分析；承载力； 结构尺寸

木质托盘对我国本来就短缺的森林资源造成大量损耗，寻求优质的代木托盘成为必然。竹质材料具有质地坚硬、成材期短、力学性能优良等特点，而且价格低廉；窝蜂结构相对质量轻，抗压、抗震性能好，竹环还可以完全循环使用，竹环蜂窝板托盘必然成为一种理想的代木托盘。20世纪20年代针对夹层结构就有学者开始研究，但把夹层理论应用于竹质蜂窝板力学性能的研究却非常少见，因此，本文的研究具有非常重要的意义。

1 夹层梁理论研究现状

窝蜂结构最早起于仿生学，以其优良的结构性能较早地应用于航空航天领域[1]。1938 年，夹层结构开始应用于德国制造的四引擎 Havilland Albatross飞机以及后来的蚊式轰炸机中的圆形机身外壳[2]。从 20世纪50 年代开始蜂窝夹层结构普遍应用于航空航天领域，对航空航天工业的发展起到了极大的贡献[3]。1969年， H.G.Allen 提出了一种简化模型[4]并得到广泛的应用。该模型假定夹芯极软，仅能抵抗横向切应力，忽略其面内弯曲刚度。这种模型的优点是将上、下蒙皮与夹芯的作用单独区分开来，在较大程度上简化了分析，但夹芯相对于蒙皮而言具有较大的厚度，忽略了其面内刚度和弯曲刚度，在一定条件下会导致较大误差。1988年， Gibson提出了胞元材料理论[5]，该理论是对蜂窝夹心面内的等效参数进行大量的研究后得出的，分析时将蜂窝夹层板简化为线弹性 Bernoulli-Euler 梁，并忽略胞壁在 x方向和y 向厚度的不一致性，然后采用材料力学的有关公式推导出解析式，结果会给蜂窝夹层板的理论研究带来一定误差。20世纪90年代，基于胞元材料理论，国内的一些学者提出了一些考虑夹芯面内刚度的蜂窝夹层板壳结构分析模型[6-7]，这些模型的共同特点是将夹芯视为服从剪切变形理论的正交各向异性层，确定了蜂窝夹芯面内等效材料参数后，再进行求解。进入21世纪，随着计算水平的提高，国内的部分学者利用3D有限元数值模拟技术， 提出了等效弹性参数的计算公式和一种循环优化设计蜂窝夹芯板厚度的新思想[8]。

2 竹环蜂窝板简介

竹环蜂窝板的结构见图1，蜂窝板总体是一个矩形结构，长和宽的长度根据上面板和下面板将竹环夹在中间，四周由封板封合[9]。上面板由竹胶板剪裁出来，四周的封板可用竹胶板或者木制材料，竹环由竹子直接切割成等高度的环即可，用胶粘剂将它们组合起来并适当加压固定后即可投入使用。整个加工过程非常简单，竹胶板直接到专业的生产商采购回来剪裁即可，竹环不需要经过特别的处理，因为竹环从它受力的贡献上讲，它只是增加了板的抗弯截面系数以及承载压力，竹环本身抗压能力就特别强，对竹环的直径大小也没有特别的要求，只要基本排满整个夹层以防止竹环脱胶后自由移动。需要注意的地方是，四周的封边一定要与上下两个面的面板胶合牢固，否则封边脱胶可能造成竹环脱离蜂窝板，使其失去承载能力[10]。

图1 竹环蜂窝板结构Fig. 1 Structure of bamboo ring honeycomb plate

3 夹层梁基本计算理论

因为是用夹层梁理论进行竹环蜂窝板受力性能的研究，所以以下将竹环蜂窝板看作蜂窝夹层梁。在进行挠度计算之前，应先计算梁的结构参数。

3.1 抗弯刚度及抗弯截面系数

根据夹层梁的弯曲变形理论，在弯曲载荷下，夹层梁的性能与“工”字梁类似，面板材料承担截面力矩，夹芯材料承担该截面的剪力（见图2）。

宽度为 b的夹层梁的抗弯刚度D由三部分组成，包括面板对截面形心轴的抗弯刚度、面板本身的抗弯刚度和夹层对截面形心轴的抗弯刚度。

图2 简化夹层梁结构Fig. 2 Simplif i ed sandwich beam structure

据此求得：

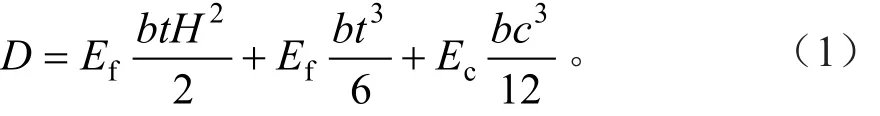
式中：Ef为竹胶板弹性模量；Ec为夹心竹环整体的弹性模量。

第一项代表面板对整个蜂窝板形心轴的抗弯刚度，第二项代表上下面板自身的抗弯刚度之和，第三项代表夹心的抗弯刚度，由于夹心是竹环依次排列后再与竹胶板粘胶在一起而构成，竹环之间并没有形成整体，因此夹心层基本不具备弹性，其弹性模量相对竹胶板的弹性模量，可以忽略，因此可将竹环蜂窝板的抗弯刚度简化为：

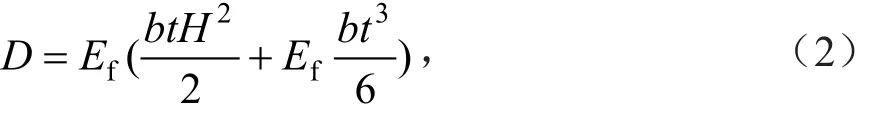
进而可得蜂窝梁的抗弯截面系数：

3.2 挠度计算

竹环蜂窝板受力后会产生变形，蜂窝板变形产生的挠度应由两部分组成，一部分是面板的弯曲挠度，另一部分是蜂窝夹芯由于剪切力产生的剪切变形而形成的剪切挠度。

（1）面板的弯曲挠度

根据材料力学弯曲挠度计算理论，对于弯曲挠度vb有：

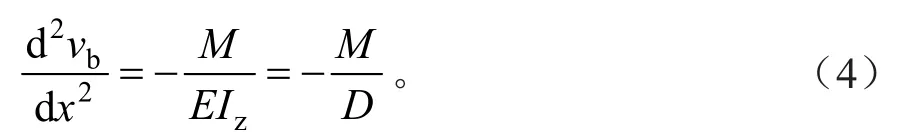
（2）剪切挠度

根据铁摩辛柯提出的剪切梁理论[11]，在蜂窝夹层板弯曲中，剪切作用产生的梁的挠度曲线的斜度近似等于中性轴的剪切应变，若用vs表示剪切单独作用产生的挠度，剪切引起的斜度为：

式中：αc为剪切系数，夹层梁中假设剪应力沿夹层均匀分布，取值为1；Q为蜂窝夹层板所受剪力；G为截面剪切模量；A为截面面积（b×h）。当梁上作用有均布载荷q时，其剪力Q是连续函数，可对x进行微分，且于是可得到：

式中：B为蜂窝梁的抗剪刚度。故竹环蜂窝梁的总挠度为：

负值表示挠度的方向向下，经过积分可以求解出蜂窝梁的总挠度，其中的积分常数需要通过蜂窝梁的支撑条件和边界条件来确定。

剪切挠度的引进能够增加计算挠度的精确性，但会使挠度的计算过程变得非常繁琐，所以在后面的挠度计算中，忽略剪切挠度，而在最后以一修正系数对只按弯曲变形计算的挠度进行修正。

4 蜂窝梁在各工况下的受力分析

4.1 在地面堆码工况下的受力分析

当蜂窝托盘放置在地面上进行堆码[12]时，根据梁式蜂窝托盘承受均布载荷时的特点，可将其简化为三点简支的梁（如图3所示）。

图3 堆码工况下的受力模型Fig. 3 Strained model under stacking conditions

忽略剪切变形的影响，根据中点挠度为0的变形协调条件，建立解一次超静定梁的方程组：

得梁的弯矩方程[13]为：

弯矩图如图4所示。

图4 梁在均布载荷下的弯矩Fig. 4 Bending moment with uniform loads

梁在x=l处有最大弯矩1ql2/8，但基于此处有支撑梁，且支撑梁具有一定宽度，蜂窝铺板此处的上表面的拉应力会比理论计算值小，最大的拉应力发生在x=3l/8和x=13l/8处的下面板上，其弯矩M=9ql2/128，则下面板内的最大拉应力为：

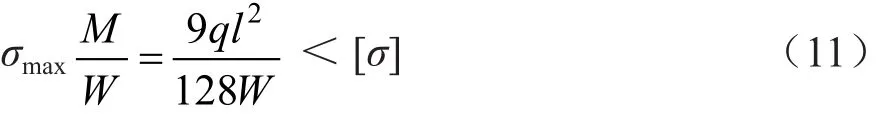
式中，[σ]为竹胶板的许用拉应力。

由图4可知，最大挠度发生在x=l/2和x=3l/2处，当0≤x≤l时，对于挠度有方程：

当x=0时，δ=0；当x=l/2时，δ′=0。代入（11），求得：

将式（12）代入式（11），得x=l/2处的挠度为：由于省略了剪切变形的影响，对此处的挠度结果加以修正，引入修正系数k1，则x=l/2处的挠度为：

式中[δ]为托盘最大许可挠度。

4.2 在叉举工况下的受力分析

叉车叉举托盘时，蜂窝梁的受力简图见图5。

可知，叉车的货叉对梁的支撑力为：

其弯矩方程为：

整个蜂窝梁的弯矩如图6所示。

图6 叉举时蜂窝梁承受的弯矩Fig. 6 Bending moment in fork lift conditions

弯矩最大值在l/2处，且Mmax=ql2/8，梁的上面板受拉，应有最大拉应力，为：

对于l/2≤x≤3l/2时，只考虑弯曲挠度，有：

当x=l/2时，δ=0；当x=l时，δ′=0，代入（15）式，得到：

将式（16）代入式（15），可得叉举时蜂窝托盘中点的挠度为：

在货叉处的斜度为：

该斜度引起的蜂窝梁外伸端部的挠度为：

蜂窝托盘梁外伸端部的总挠度为：

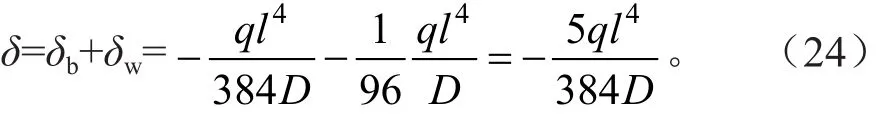
式中：δb为蜂窝外伸梁在均布载荷q下的挠度。

对比式（17）和（20），可知叉举时蜂窝托盘梁的两端部挠度比托盘中点挠度大，因此进行挠度校核时，应以端部挠度作为比较量。引进修正系数k2对端部挠度进行修正，即：

式中，k2通过实验获取。

5 有效设计方程的提取

根据以上的分析，提取式（11）、（15）、（18）、（25），可以得到如下方程组：

对比方程①和方程③，可知若方程③成立，方程①必然也成立，所以方程③是有效式；一般由剪切产生的挠度很小，理论上修正系数k1、k2相差不会很大，方程②的有效性高于方程④的有效性，但为保证理论的严谨性，对方程②和方程④在修正系数未知前，不作取舍。所以方程组（26）中有效的方程是②、③、④。

若通过试验和理论对比后，获得了修正系数k1、k2，并测出竹胶板的弹性模量，由于蜂窝板的长、宽、承受载荷和最大许可应力、最大许可挠度是按设计要求给定的，因此根据式（26）可以获得理论上的蜂窝板的最低厚度。

6 结 语

本论文探讨的是承受均布载荷作用下的竹环蜂窝托盘的设计理论，该理论最终得到了一个有效的不等式方程组，通过对该方程组的求解可以获得要求载荷下蜂窝板的最低厚度。本论文的设计理论是基于实验的基础上的，如果考虑剪切变形产生的挠度，将使设计理论变得十分复杂，降低了该理论的可读性和实用性，因此本设计理论引进了修正系数，通过实验的方式对仅依据弯曲变形计算出的挠度进行了修正，提高了理论的可信度和权威性。遗憾之处是条件所限，实验暂未能实行，期待进一步的研究。

[1] Robinson M J.运载火箭用的先进复合材料结构[J].国外导弹与航天运载器，1992,17(6)：45-49.

[2] Allen H G. Sandwich Constructions Today and Tomorrow[J].Sandwich Construction,1988,27(6)：12-18.

[3] 赵金森. 铝蜂窝夹层板的力学性能等效模型研究[D].南京：南京航空航天大学，2006.

[4] Allen H G. Analysis and Design of Structural Panels[M]. Oxford,Pergamon Press, 1969.

[5] Gibson L J A, Shby M F. Cellular Solids, Structure and Properties[M]. Oxford： Pergamon Press,1988.

[6] 富明慧，尹久仁.蜂窝芯层的等效力学参数[J].力学学报，1999，31(1)：23-29.

[7] 王颖坚.蜂窝结构在面内剪切作用下的变形模式[J].北京大学学报，1991，27(4)：56-59.

[8] 梁 森. 蜂窝夹芯结构面内等效弹性参数的分析研究[J].航空材料学报，2004，24(3)：38-43.

[9] 铁摩辛柯 S，盖尔 J.材料力学[M].北京：科学出版社，1978.

[10] 田 莉,袁茂强,马庆勇,等.南方高杆芦苇收割装备的适应性设计与探讨[J].中南林业科技大学学报，2011,31(11)： 159-162.

[11] 刘 旭,钟红燕,袁茂强,等.糟渣类高湿物料干制工艺和设备的研究[J].中南林业科技大学学报，2009,29(2)：128-132.

[12] 朱永辉.蜂窝纸基托盘静载特性研究[D].无锡：江南大学，2009.

[13] 刘鸿文.材料力学[M].北京：高等教育出版社，2003.

Study on design theory of bamboo ring honeycomb plate tray

PANG Yan, YIN Qian-cai, ZENG Guang
(School of Transportation and Logistics, Central South University of Forestry & Technology, Changsha 410004, Hunan, China)

Bamboo ring honeycomb plate tray is a new type of composite structure pallet, and a kind of very potential application tray because it perfectly merges the advantages of bamboo with honeycomb structure advantages together. However, there is few design theory research about bamboo ring honeycomb tray. The design theory of bamboo ring honeycomb plate was studied through the experiments and by using sandwich beam theory, and the design model about the relationship of the tray bearing capacity and tray structure size were built. Thus laying a theoretical basis for realizing honeycomb plate tray industrialization.

bamboo ring honeycomb plate tray; design theory; mechanical performance analysis; bearing capacity; physical dimension

S781.69

A

1673-923X(2013)03-0103-04

2012-10-10

湖南省自然科学基金项目“新型竹质通用平托盘力学性能研究”（11JJ2017）

庞 燕（1965-），女，湖南湘潭人，教授，博士，主要研究方向：物流工程与管理

[本文编校：谢荣秀]