基于到达时间差的两步最小二乘定位算法

谢胜东 胡爱群 黄 毅 姜 禹

(1东南大学信息科学与工程学院, 南京 210096)

(2南京信息工程大学计算机与软件学院, 南京 210044)

自1996年美国联邦通信委员会要求无线蜂窝系统必须能够对发出紧急呼叫的移动用户实现定位后,定位技术便吸引了众多学者的关注,并得到了迅速发展．现有定位技术可以分为基于信号强度(RSS)的定位[1]、基于信号到达时间(TOA)[2]或时间差(TDOA)的定位[3],以及基于信号到达角度(DOA)的定位[4]．由于TOA或TDOA能以稍微复杂的硬件电路来换取较高的定位精度,具有RSS和DOA两者的优点,因此被广泛应用于GSM，LTE等系统中．

TDOA定位主要采用约束线性最小二乘(CLS)算法,此类算法经历了3个发展阶段.第1阶段为非全局最优阶段,即无法获得目标函数的全局最优值．例如,Schau等[5]提出的球面相交法(SX)获得了CLS退化问题的一个全局最优解,然而该全局解并不是原始CLS的最优解．Chan等[6]提出的二次纠正最小二乘法(QCLS)通过第1次丢弃约束条件以及第2次将严格约束条件松弛为最小二乘意义上的约束条件来估计目标节点的位置,由于采用了加权,使得其性能优于SX．第2阶段为全局最优阶段,在该阶段中,算法能够获得目标函数的全局最优解．例如,Huang等[7]基于拉格朗日乘子法提出的线性纠正最小二乘法(LCLS)以及Amir等[8]利用广义信任域法(GTRS)分别获得了CLS的全局最优解．第3阶段为总体最小非全局最优阶段．事实上,由于基于最小二乘TDOA定位算法中不相容矩阵的元素存在误差,因此这类算法不再属于CLS问题,而是一个约束总体最小二乘(TLS)问题,上述所有算法的解都不再是TLS问题的最优解．为此,Weng等[9]在丢弃约束条件的基础上,给出了TLS问题的封闭解;Yang等[10]提出了基于牛顿迭代法的约束总体最小二乘定位算法(CTLS),从而获得了目标节点的位置估计值的局部最优解;Cao等[11]在CTLS算法的基础上引入了权重因子,提出了加权约束总体最小二乘定位法(WCTLS),进一步提高了CTLS算法的估计性能．

然而,在目标节点到达不同基站的距离差上,CTLS与WCTLS均使用测量值来代替实际值,当测量误差较大时,会对定位效果产生严重的影响．为解决上述问题,本文提出了一种两步最小二乘定位算法(TSLS),即首先利用LCLS算法对目标位置进行初次估计,从而计算出目标节点到达不同基站的距离差,并用该距离差来近似实际距离差,最后利用CTLS算法来对目标位置再次进行估计．

1 系统模型

本文以二维空间中的目标为定位对象．假设在二维空间中,存在N+1个基站,第0个基站为参考基站,其坐标为(x0,y0),其余基站的坐标记为(xi,yi),i=1,2,…,N;同时存在一个位置未知的目标节点,其坐标记为(x,y)．尽管本文研究的是二维空间中的定位方法,但该方法很容易扩展到三维空间．

通过TDOA测量,可以得到目标节点到达基站i与基站0之间的时间差ti,0,该时间差乘以信号的传播速度,即可获得目标节点到达基站i与基站0之间的距离差ri,0．由于信号传播速度固定,因此下文用距离差来代替时间差．距离差ri,0的表达式为

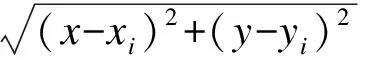
(1)

式中,ri表示目标节点到达基站i的距离．

将式(1)中r0移到等号左边,并对等号两侧进行平方运算后可得

(2)

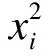
(3)

写成矩阵形式为

Aθ=b

(4)

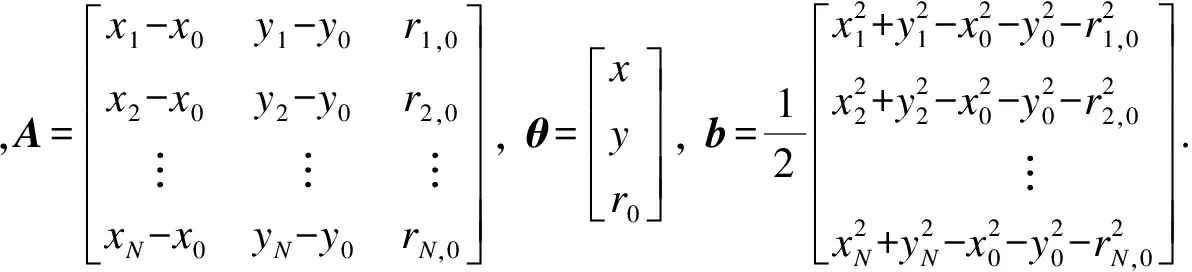
2 两步最小二乘定位算法

对式(4)进行观察不难发现:由于矩阵A和向量b中均存在需要通过测量才能得到其值的元素ri,0,i=1,2,…,N,因此矩阵A和向量b中均存在误差,于是对式(4)的求解将不再是一个普通的约束最小二乘问题,而属于总体最小二乘问题．

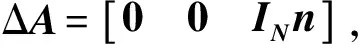
(5)

当n的每个元素均远小于其对应的距离差时,则可忽略n的二次方所带来的影响,故式(5)可近似写成

(6)

令G=r1IN+diag([r1,0r2,0…rN,0]),基于约束完全最小二乘的相关理论[12],目标节点的位置则为如下问题的解:

(7)

然而,矩阵G和向量Aθ-b均含有元素ri,0,式(7)中的约束条件本质上同样具备总体最小二乘的形式．如果直接采用CTLS算法[10],即将约束条件看成普通最小二乘形式,忽略矩阵G中的误差,而令n=G†(Aθ-b),其中“†”表示伪逆,那么将降低位置估计的精度．

显然,减少矩阵G中的元素误差必然可以提高CTLS算法的估计精度．为了减少该误差,须尽可能准确地获得目标节点到达不同基站的距离差．为此,本文提出采用计算距离差来代替测量距离差．如果计算距离差的精度大于测量距离差,那么必然能够减少矩阵G中的误差,从而提高CTLS算法的估计精度．为此,需要尽可能准确地估计出目标节点的位置．

考虑到LCLS算法[7]能够获得普通约束最小二乘模型中目标函数的最优解,因此,本文采用LCLS算法来对目标节点的位置进行初步估计．根据LCLS算法,目标节点的位置可以通过最小化拉格朗日函数L(θ,λ)得到,即

L(θ,λ)=(Aθ-b)T(Aθ-b)+λθTΣθ

(8)

其中,Σ=diag(1,1,-1)．将L对θ以及λ求导,并令求导结果为0,通过求解方程组,可获得有限个满足条件的θ和λ的值,将这些值代入到式(8)中,使得拉格朗日函数最小的θ中的前2个元素即为目标节点位置的估计值．

在获得目标节点位置的估计值后,可利用式(1)计算出目标节点到达不同基站的距离差．将该距离差代入到矩阵G中,同时将式(7)中的约束条件看成普通最小二乘形式,令n=G†(Aθ-b),从而目标节点的位置为式(9)的解[10],即

F(ϑ)=(A1ϑ+A2(ϑTϑ)1/2-b)T(GGT)-1·
(A1ϑ+A2(ϑTϑ)1/2-b)

(9)

式中,ϑ={x,y}T;A1为A的前2列;A2为A的第3列．式(9)是一个非线性最优化问题,由于前面已经利用LCLS算法对目标节点位置进行了估计,因此可将该估计值作为式(9)的初始点,利用牛顿迭代法即可获得式(9)的局部最优解,从而获得目标节点的位置．

从过程上看,本文的两步最小二乘定位算法首先利用LCLS算法来初次对目标节点的位置进行估计,从而计算出目标节点到达不同基站的距离差;接着再利用CTLS算法来对目标节点的位置进行二次估计．但从本质上讲,TSLS是通过减少CTLS中矩阵G的误差来提高其位置估计精度,因此可以看成是一种增强型CTLS算法．

3 性能分析

本文的仿真环境参考文献[10]．在一个100m×100m的二维矩形区域中,存在一个目标节点,其坐标为(42,12)m,同时存在10个基站,其坐标分别为(0,0)、(16,42)、(34,52)、(58,30)、(78,18)、(66,48)、(30,-12)、(22,12)、(57,-3)、(12,-28)m．在仿真中,基站按照上述顺序,从4个逐渐增加到10个．TDOA测量噪声服从0均值,方差为δ2的高斯分布．

在仿真图中,测量噪声方差为10lgδ2．用定位误差e来衡量算法的性能,其计算公式为

(10)

图1是基站数目分别为5,7,9,TDOA测量噪声方差从0dB变化到20dB时3种算法的定位误差．从图中可以看到，TSLS算法的性能始终优于CTLS算法，这主要是因为在上述情况下,通过LCLS算法获得的计算距离差的精度高于测量值.但当测量噪声大于18dB时,TSLS的性能存在下降的趋势．这是因为在式(6)中,CTLS算法忽略了测量误差的二次项,当测量误差变大时,忽略该二次项而带来的影响也会逐渐增加,从而导致CTLS算法不适合高测量误差的情况,进而引起TSLS算法性能的下降．尽管如此,TSLS算法的性能始终优于CTLS算法．

图2是在TDOA测量噪声方差分别为5,10,15dB,基站数目从4个逐渐增加到10个时不同算法的定位误差．从图中可以看到:① 当基站数目为4时,TSLS算法的性能逊于CTLS算法,而其余情况下TSLS算法的性能都优于CTLS算法．这是因为在基站个数较少的情况下,LCLS算法的定位误差较大,从而导致计算距离差的精度小于测量值,使得式(7)矩阵G中的误差增加,导致TSLS算法的性能下降．但随着基站数的增加,LCLS算法定位精度也随之增加,因此减少了矩阵G中的误差,从而使得TSLS算法的性能得到迅速提高.② 当基站数为6时,TSLS算法的性能逊于LCLS算法,而其余情况下TSLS算法的性能都优于LCLS算法．这是因为基站的分布会对CTLS算法忽略式(6)中测量误差二次项后的性能产生影响[13],但这种影响并不显著,从图中可以看到TSLS算法的性能只是略逊于LCLS算法．总体而言,TSLS算法的性能要优于LCLS和CTLS算法．

图1 不同TDOA测量噪声方差下的定位误差

图2 不同基站数下的定位误差

4 结语

为了提高CTLS算法的性能,本文提出了TSLS算法．该算法首先通过LCLS算法对目标节点的位置进行估计,进而利用估计值来计算目标节点到达不同基站的距离差,并将该计算值来代替测量值,最后通过CTLS算法再次估计目标节点的位置．本质上讲,由于TSLS算法减少了CTLS算法中矩阵的误差,从而提高了其性能,因此是一种增强型CTLS算法．仿真结果表明,当TDOA测量噪声小于18dB时,TSLS算法总体上的性能要优于CTLS算法和LCLS算法．

)

[1] Liu C, Fang D Y, Yang Z, et al. RDL: a novel approach for passive object localization in WSN based on RSSI [C]//IEEE2012InternationalConferenceonCommunications. Ottawa, Canada, 2012: 586-590.

[2] Ma Z H, Ho K C. TOA localization in the presence of random sensor position errors [C]//Proceedingsofthe2011IEEEInternationalConferenceonAcoustics,Speech,andSignalProcessing. Prague, Czech Republic, 2011: 2468-2471.

[3] Qu X M, Xie L H. Source localization by TDOA with random sensor position errors—part Ⅱ: mobile sensors [C]//15thInternationalConferenceonInformationFusion. Singapore, 2012: 54-59.

[4] Jonathan B, Anne F, Pascal L. A space time array processing for passive geolocalization of radio transmitters [C]//Proceedingsofthe2011IEEEInternationalConferenceonAcoustics,Speech,andSignalProcessing. Prague, Czech Republic, 2011: 2596-2599.

[5] Schau H C, Bobinson A Z. Passive source localization employing intersecting spherical surfaces from time of arrival differences [J].IEEETransactionsonAcousticsSpeechandSignalProcessing, 1987,35(8): 1223-1225.

[6] Chan Y T, Ho K C. A simple and efficient estimator for hyperbolic location [J].IEEETransactionsonSignalProcessing, 1994,42(8): 1905-1915.

[7] Huang Y, Elko G W, Mersereau R M. Real time passive source localization: a practical linear correction least squares approach [J].IEEETransactionsonSpeechandAudioProcessing, 2001,9(8): 943-956.

[8] Amir B, Petre S, Li J. Exact and approximate solutions of source localization problems [J].IEEETransactionsonSignalProcessing, 2008,56(5): 1770-1778.

[9] Weng Y, Xiao W D, Xie L H. Total least squares method for robust source localization in sensor networks using TDOA measurements [J].InternationalJournalofDistributedSensorNetworks, 2011,2011: 172902-01-172902-08.

[10] Yang K, An J P, Bu X Y, et al. Constrained total least squares location algorithm using time difference of arrival measurements[J].IEEETransactionsonVehicularTechnology, 2010,59(3): 1558-1562.

[11] Cao J M, Wei H W, Yu J. Weighted constrained total least square algorithm for source localization using TDOA measurements [J].FutureWirelessNetworksandInformationSystems, 2012,143: 739-746.

[12] Golub G H, Loan C F V. An analysis of the total least squares problem [J].SIAMJNumerAnal, 1980,17(6): 883-893.

[13] Xu B, Qi W D, Wei L, et al. Turbo TSWLS: enhanced two-step weighted least squares estimator for TDOA based localization [J].ElectronicsLetters, 2012,48(25): 1597-1598.