六自由度并联机器人结构运动的分析研究
2013-12-23赵良伟王惠源刘鹏展兰晓龙
赵良伟,王惠源,刘鹏展,陆 明,兰晓龙
(中北大学 机电工程学院,山西 太原 030051)
0 引言
机器人的产生主要是为了满足一些高难度的作业要求。机器人有串、并联之分,串联机器人主要包括支架(也就是基座部分)和手臂部分(大臂、小臂),然后采用各种运动副连接而成,其结构形式是串接而成的;并联机器人结构包括动平台、静平台、滑块、立柱以及相应的连接副,主要使用一些万向铰链连接而成。对串联机器人进行位置的求解比较容易,而对并联机器人进行正解是比较困难的,但是,并联机器人也有其自身的优点,那就是很容易进行位置的逆解[1]。当已知机器人从动件的一个位置,反解出机器人原动件也就是控制部分所需要的位移量是很容易的。本文利用UG软件进行了六自由度并联机器人模型的建立,然后以实际模型尺寸为基础进行了位置逆解运算的推导。
1 六自由度并联机器人结构原理
并联机器人的主体部分包括[2]床身部分、连杆部分和活动平台。活动平台与6个连杆用虎克铰联接,6个连杆再与6个滑块采用虎克铰联接(当然也可以采用球铰联接,本模型采用虎克铰),滑块与滚珠丝杠联接,通过电机驱动滚珠丝杠的运动带动滑块沿滚珠丝杠的轴线方向运动,从而改变6个连杆的位置使动平台运动,在动平台上可以安装各种其他的机械,以满足不同的工作要求。直接驱动动平台运动的是6 根连杆,而连杆是由6个步进电机驱动的,由于6个步进电机是独立控制的,因此此机器人可以实现6自由度的运动,在安装形式上采用的是并联[3]形式。
2 六自由度并联机器人结构模型的建立
对于本模型而言,我们采用以下的结构形式[4]:固定支座部分采用3块立板结构,并在立板内部设有导槽,滑块可以在导槽内滑动,6块滑块与6根连杆相联接,6根连杆与活动平台相联接,联接部分采用虎克铰形式,滑块与滚珠丝杠构成滚珠丝杠螺母副,然后通过6个步进电机分别驱动6根滚珠丝杠运动。六自由度并联机器人结构模型如图1所示。并联机器人的总体结构参数如图2所示。

图1 六自由度并联机器人结构模型
3 并联机器人位置运动计算与分析研究
对于此结构,主要是根据某一时刻动平台的位置来确定要达到此位置时各电机输出的参数,即所谓的位置反解。以建立的实体模型尺寸为基础依据,为求滑块位置,首先建立动、静两个坐标系[5],静坐标系原点O′位于上平台所构成的平面中心,动坐标系原点O位于下平台中心,如图3所示。其中,Bi(i=1,2,…,6)为上虎克铰的几何中心,Pi为下虎克铰的几何中心(i=1,2,…,6)。
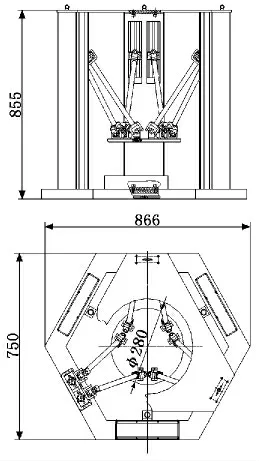
图2 六自由度机器人总体结构尺寸

图3 坐标系示意图
根据建立的实体模型,我们设定上、下虎克铰中心所在平面间的距离为330mm。对上虎克铰中心,有:
∠B1O′B2=30°,∠B3O′B4=30°,∠B5O′B6=30°。
对下虎克铰中心,有:
∠P2OP3=40°,∠P4OP5=40°,∠P6OP1=40°。
上平台虎克铰几何中心所在圆直径为Φ490mm,下平台虎克铰几何中心所在圆直径为Φ200mm。
3.1 初始条件的确立
依据机构的基本尺寸,在所建立的坐标系上,由几何关系可求出上、下平台各个铰点Bi和Pi(i=1,2,…,6)的坐标值。经计算得:
B1=(63.4,236.7,0),
B2=(-63.4,236.7,0),
B3=(-276.3,-63.4,0),
B4=(-173.2,-173.2,0),
B5=(173.2,-173.2,0),
B6=(276.3,-63.4,0),
P1=(64.3,76.6,-330),
P2=(-63.4,76.6,-330),
P3=(-98.5,17.4,0),
P4=(-34.2,-94,-330),
P5=(34.2,-94,-330),
P6=(98.5,17.4,-330)。
3.2 空间变换矩阵的求解
假定动坐标系沿定坐标系的X、Y、Z 轴分别平移XP、YP、ZP后,再在新的坐标系下绕X 轴旋转α,绕Y轴旋转β,绕Z 轴旋转γ,则坐标变换矩阵[6]为:
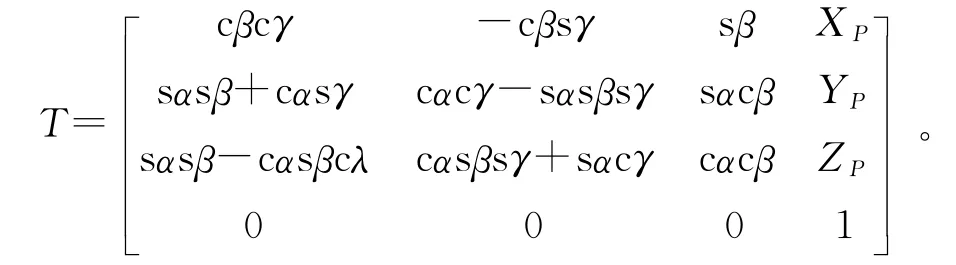
其中:cα=cosα;sα=sinα;其他依此类推。随着滑块的移动,活动平台各铰点Pi也随之到达新的位置,设P′i为Pi到达新位置时的坐标值,则有P′i=TPi。根据此模型技术参数中运动平台的动作范围,不妨假定运动平台处于其中一极限位置时有XP=YP=ZP=100 mm;α=β=γ=15°,于是计算可得:

3.3 新坐标及各轴滑块移动量的计算
3.3.1 计算新坐标

P′1=(55.37,272.92,-195.01)。
同理可得:
P′2=(-64.61,232.41,-172.51),
P′3=(-81.72,167.41,-185.17),
P′4=(6.12,85.62,-213.52),
P′5=(69.94,107.17,-243.49),
P′6=(102.08,229.47,-219.65)。
3.3.2 求P′i到Di的距离SAi和Di到Bi的距离SBi
图4为一条传动链上各点的几何关系图。
在图4中,Bi和Ci分别表示活动平台在初始位置时和到达目标位置时滑块中心停留的位置,BiDi是与Z 轴平行且经过Bi点的直线,P′iDi垂直于BiDi,垂足为Di(i=1,2,…,6),则可构建出一个直角三角形BiP′iDi,由于BiDi平行于静坐标系的Z′轴,因此Di与Bi仅Z 轴 坐 标 不 同,即XDi=XBi,YDi=YBi,Z′Pi=ZDi,根据图4得:

代入相 关 数 据 可 求 得:SA1=37.10 mm,SA2=4.46mm,SA3=278.01mm,SA4=314.87 mm,SA5=298.78mm,SA6=322.33mm。
同理,可 求 得:SB1=195.01 mm,SB2=172.51 mm,SB3=185.17mm,SB4=231.52mm,SB5=243.49 mm,SB6=219.65mm。

图4 几何关系示意图
3.3.3 求Ci到Di的距离SCi
根据图4几何关系示意图可知,P′i到Ci的距离为上、下虎克铰中心的距离,记为S。根据图4得:

3.3.4 求各轴上滑块的移动量ΔSi
ΔSi可表示为:
ΔSi=SCi-SBi。
代入相关数据可求得:
ΔS1=365.43-195.01=170.42mm,
ΔS2=366.78-172.51=194.27mm,
ΔS3=239.28-185.17=54.11mm,
ΔS4=188.15-231.52=-43.37mm,
ΔS5=212.77-243.49=-30.72mm,
ΔS6=175.06-219.65=-44.59mm。
以上计算结果中,“-”值表示沿Z 轴负方向移动;反之则表示沿Z 轴正方向移动。
通过上述计算,我们根据某一时刻动平台的位置,确定了要达到此位置时各点电机的输出参数。
4 结论
本文以实际的六自由度并联机器人模型为研究对象,通过建立起的六自由度并联机器人实体结构模型,确定出了原动件的运动规律,找到一个适合此六自由度并联问题模型的求解方法,有助于控制方案的设计以及实现,也可以在此基础上去设计更加实用的结构,并对以后的应用具有一定的指导意义。
[1] 刘国平,李建武.6PTRT 并联机器人一种逆解算法研究[M].南昌:南昌大学出版社,2009.
[2] 黄真.并联机器人机构学理论及控制[M].北京:机械工业出版社,1997.
[3] 张曙,并联运动机床[M].北京:机械工业出版社,2003.
[4] Wang Yongbo,Pessi Pekka,Wu Huapeng,et al.Accuracy analysis of hybrid parallel robot for the assembling of ITER[J].Fusion Engineering and Design,2009,84:1964-1968.
[5] Lu Yi.Simulation of machining 3Dfree-form surface in normal direction using 6-SSP and 4SPS+UPU parallel machine tools[J].J Adv Manuf Technol,2007,33:1180-1188.
[6] 黄真,赵永生,赵铁石.高等空间机构学[M].北京:高等教育出版社,2006.
