一种单力臂机械系统的鲁棒自适应控制
2013-12-23盛晨函
盛晨函,曾 忠
(上海理工大学 机械工程学院,上海 200093)
0 引言
高精度单机械臂系统是一种典型的伺服系统,在实际应用中该系统的跟踪性能会受到非线性摩擦环节的影响[1]。摩擦现象是一种非线性的、具有不确定性的自然现象。对于高精度机械伺服系统,摩擦环节成为提高系统性能的障碍,主要表现为在低速时出现爬行现象、稳态时有较大的静差或出现极限环振荡[2]。从控制角度来说,为了减轻摩擦环节带来的负面影响,可以采用模型参考自适应控制方法[3]。本文采用基于李雅普诺夫直接法的鲁棒模型参考自适应控制,在具有参数不确定性和未知非线性摩擦特性的情况下,使系统的跟踪误差趋于零,并具有良好的鲁棒性。
1 不确定单力臂机械系统摩擦模型
具有参数不确定性的单力臂机械系统模型为[4]:
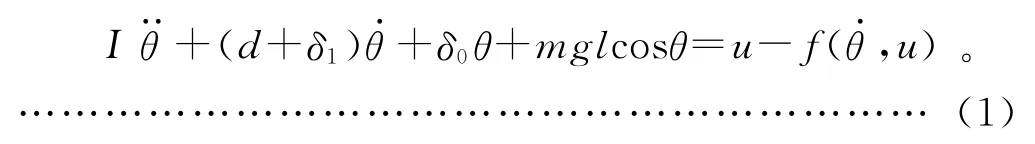

如果机械臂的运动平面与水平面平行,则方程中的重力项可以忽略,式(1)变为:

采用二阶微分方程描述为:


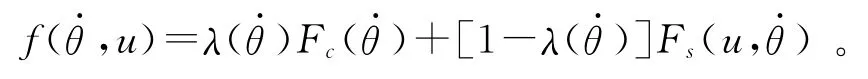

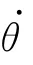

对于式(3)的系统,引入稳定的参考模型为:

其中:θm为模型输出;r为系统指令输入;a1、a0、b均为正实数。定义误差信号为:

则控制的问题在于寻求控制u,使得对于任意初态,跟踪误差e(t)满足:

2 不确定单力臂机械系统鲁棒自适应控制
2.1 控制器设计
结合式(3)和式(8),得被控对象动态方程为:

其关于误差e的动态方程为:



定义辅助信号e^为:

取控制率u为:

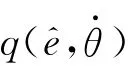
2.2 稳定性分析
根据参考文献[6],有如下定理:针对系统式(13),采用控制律式(16),增益系数自适应律和鲁棒补偿项设计为:
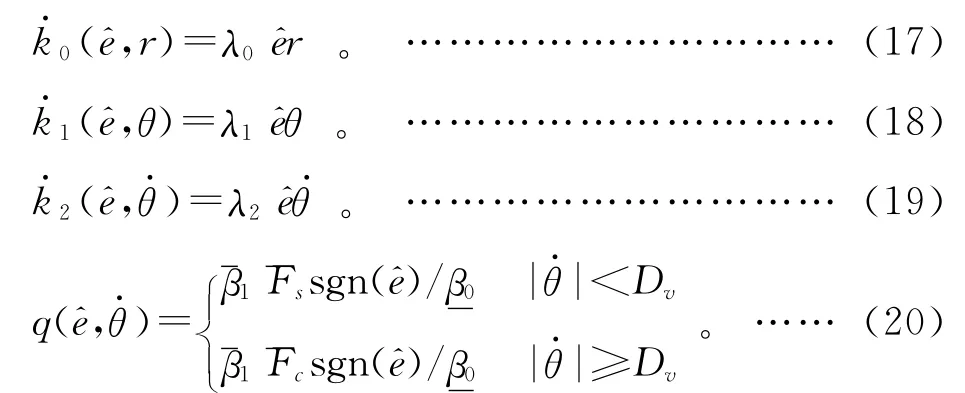
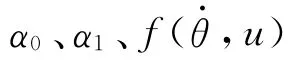
定义李雅普诺夫函数为:

由式(13)和式(14)得:
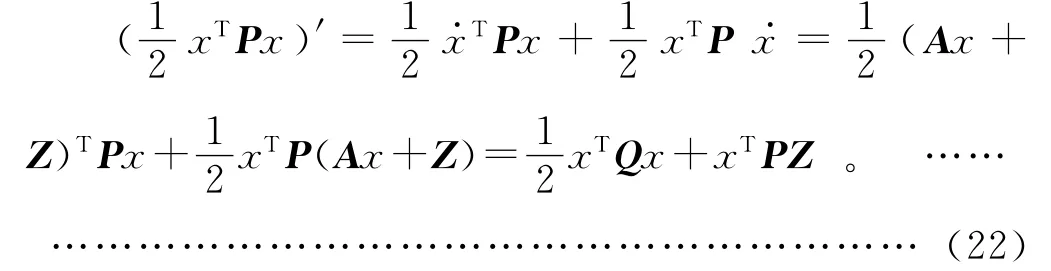
由式(13)知:

对V 取关于时间t的导数:
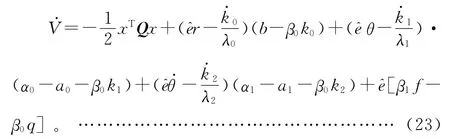
将式(17)~式(19)代入式(23),得:
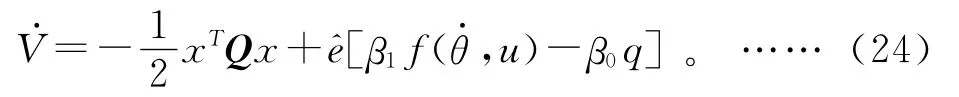

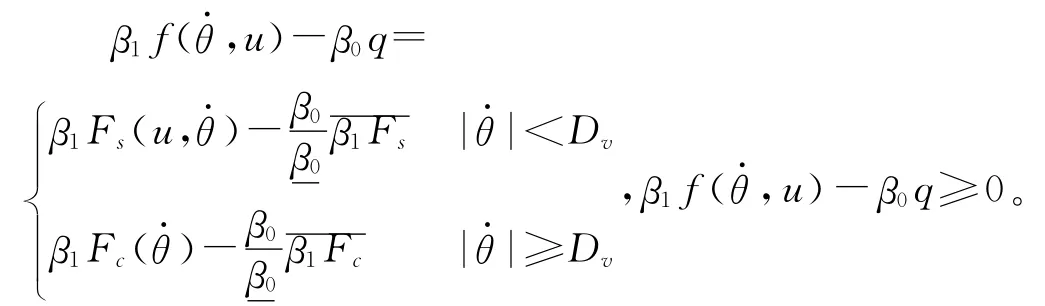
所以:
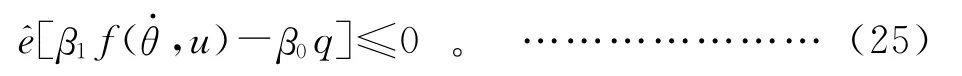
故:

其中:σm(Q)为矩阵Q 的最大值;σM(P)为矩阵P 的最小奇异值;‖·‖为2范数。由式(26)知:
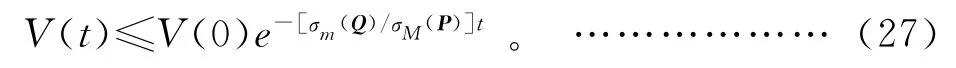
所以:
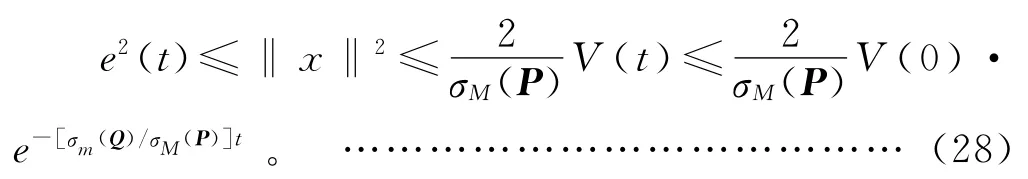
由式(26)和式(28)知,当t≥0时,对于任意的初始条件,误差e(t)是有界的,且渐近稳定。
3 仿真分析
被控对象动态方程为:



式(8)中的模型参数分别取:a1=10,a0=20,b=30,r=sgm(cos(0.05πt)),则参考模型为:


仿真结果如图2所示。结果表明,所采用的鲁棒模型参考自适应控制器适应未知摩擦特性和参数的不确定性,并能保证对象和模型的高精度跟踪位置信号。
4 结论
本文研究了一种基于鲁棒模型参考的自适应控制策略,在具有不确定摩擦特性的情况下,将其应用于不确定性单力臂机械系统的轨迹跟踪控制。无需建立摩擦模型和精确的摩擦参数,而只需要动、静摩擦的上界值。仿真结果表明,该控制器增强了系统的自适应能力,对不确定性单力臂机械系统实现了鲁棒自适应控制。
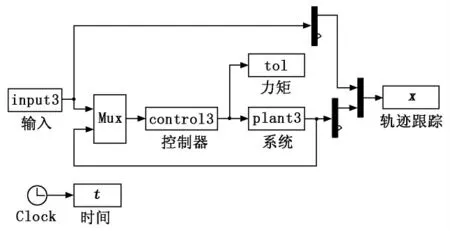
图1 不确定单力臂机械系统鲁棒自适应控制系统框图

图2 关节位置跟踪图
[1] 刘金琨.机器人控制系统的设计与MATLAB仿真[M].北京:清华大学出版社,2008.
[2] 张彦军,于国祥.滑模控制在低速摩擦伺服系统中的应用[J].控制系统,2007,23(34):45-47.
[3] 韩正之,陈彭年,陈树中.自适应控制[M].北京:清华大学出版社,2011.
[4] 申铁龙.机器人鲁棒控制基础[M].北京:清华大学出版社,2000.
[5] Shen T L,Tamura K.Robust nonlinear control of parametric uncertain systems with unknown friction and its application to a pneumatic control valve[J].Journal of Dynamic Systems,Measurement,and Control,2000,122:257-262.
[6] 刘强,扈宏杰,刘金琨.高精度飞行仿真转台的鲁棒自适应控制[J].系统工程与电子技术,2001,23(10):35-38.
