计算天然气偏差因子的DAK方法的修正

胡建国，郭分乔，许进进

(中国石化石油勘探开发研究院，北京100083)

天然气偏差因子是定量描述真实气体(天然气)与理想气体偏差程度大小的系数，是天然气其他物性计算、天然气藏地质储量计算以及管道天然气流量设计的一项相当重要的参数。天然气偏差因子过去基本上是由Standing-Katz 偏差因子图版读值得到。但这样获得天然气偏差因子十分不便，而且精度也难保证。为此，众多研究者提出了多种确定天然气偏差因子的相关经验方法［1-5］。

1959年Gray 和Sims 首先提出了数值计算天然气偏差因子的方法［6］，他们将Standing-Katz 偏差因子的值建立了一个20 ×20 的矩阵，再应用插值的方法确定不同拟对比压力、拟对比温度下的偏差因子值。这种方法受插值方法的限制，精度较差。1964年Leung 提出了应用多项式拟合偏差因子的方法，开创了应用数理统计方法研究天然气偏差因子计算的先例。此后相继出现了多种基于经验统计的偏差因子计算方法［5］。

1969年Hankinson 等人使用BWR (Benedict-Webb-Rubin)状态方程描述偏差因子的值。他们第一次将状态方程引入天然气偏差因子的计算中，应用Standing-Katz 偏差因子数值研究了BWR状态方程的系数，并在拟对比压力pr＜5.0 和pr≥5.0 的区间上分别得到BWR 方程的系数［7］。实践证明，Hankinson 等人提出的方法尽管应用了状态方程计算天然气偏差因子，但计算误差仍很大。1973年Hall 和Yarborough 以不太为人熟悉的Starling-Carnahan 的真实气体偏差因子的状态方程为基础，建立了偏差因子计算方法［8］。该方法尽管偏差因子计算的精度明显优于Hankinson 等人的方法，但在某些范围内计算误差依然很大。1974年Dranchuk 等人应用1 500 个原始的Standing-Katz 偏差因子数据，使SH-BWR(Starling-Han修正的Benedict-Webb-Rubin)状态方程与Z =f(pr，Tr)面相拟合，得到8 个系数的SH-BWR 状态方程计算偏差因子的方法，这一方法明显改善了偏差因子的计算精度［9］。1975年Dranchuk 等人又以Starling 和Carnahan 修正的BWR 状态方程为基础，建立了11 个系数的SC-BWR 状态方程计算偏差因子的方法(以下简称DAK 法)［10］，这一方法较前面任何方法的精度都高［5］。近年来又发表了几种新方法［11～14］。

在国内，李相方等人认为，在高压下天然气偏差因子随拟对比压力呈线性变化。他们基于这一规律建立了适于pr＞8 的天然气偏差因子计算方法［15］。事实上，通过对高压时Standing-Katz 偏差因子图版(pr＞15)［1］的研究(图1)，即使在高压下天然气偏差因子并不是严格随拟对比压力呈线性变化，而存在微小的曲率，因此计算精度很难保证。

图1 高压时天然气偏差因子［1］Fig.1 Z-factor for natural gas under high pressure［1］

为了提高天然气偏差因子的计算精度，不同的作者使用了不同的技巧，形成了多种方法。其中，DAK 法具有最高的计算精度，目前在各类天然气藏得到相当广泛的应用，并已成为天然气偏差因子计算的标准方法。然而，通过对DAK 法研究，当压力和温度均较高时，DAK 法计算结果误差仍较大，依然存在进一步提高计算精度的空间。通过对DAK 方法的参数进行修正，进一步提高了DAK 方法计算天然气偏差因子的精度。并应用二维平面等值线图的方法［12，14，16］，由等压线和等温线构建二维平面，分析计算结果的相对误差。结果表明，DAK 方法经过修正后，明显改善了天然气偏差因子的计算精度。

1 DAK 方法描述

Dranchuk 和Abou-Kassem(DAK)以Starling 和Carnahan 修正的BWR 状态方程为基础，应用1 500个原始的Standing-Katz 偏差因子数据，进行非线性回归分析，建立了11 系数的SC-BWR 状态方程计算偏差因子的方法［11］。由于在拟合偏差因子时有更大的自由度，使计算结果的精度更好。

DAK 模型可描述为:

式中:Tr为天然气拟对比温度;pr为拟对比压力;ρr为天然气拟对比密度;Z 为天然气偏差因子;a1—a11为系数(在原DAK 模型中各值分别为:a1= 0.326 5， a2=－1.070 0， a3=－0.533 9，a4= 0.015 69， a5=－0.051 65， a6= 0.547 5，a7=－0.736 1， a8= 0.184 4， a9= 0.105 6，a10= 0.613 4， a11= 0.721 0)。

由于式(1)所示的DAK 方法是一非线性隐式方程，通常可以应用Newton-Raphson 迭代法求解。求解过程分4 步。

第一步:假定偏差因子Z 的初值Zi，并由式(5)计算ρr。

第二步:分别由式(6)和(7)计算fi及其导数f＇i:

第三步:用Newton-Raphson 迭代公式［式(8)］修正ρr:

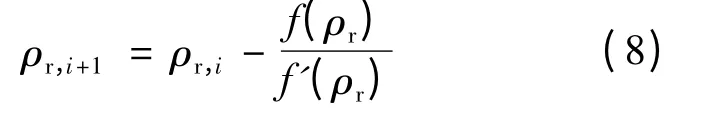
第四步:用修正的ρr重新计算Z，并代替新的Z:

然后再重复第二步直至得到满意的结果。

Newton-Raphson 迭代法求解上述问题，由于收敛很快，一般迭代3～4 次即可达到预定的精度。

2 DAK 方法的修正

为了分析DAK 方法计算天然气偏差因子的误差分布，选用了6 548 组Standing-Katz 图版数据，这些数据取自Katz 和Smith 的著作［1-2］。其中pr≤15.0 的数据取自文献［1］的表A-2 及文献［2］的表A-3，计5 940 组数据。pr＞15.0 的数据直接由图1 读取。该图直接取自Katz 的图书，未经过转载，未出现图形失真、变形，读取的数据应该是可靠的。图中8 条线，每条线上按Δpr=0.2的间隔取值，每条线取值76 个，共计读取608 组数据。这些数据为分析DAK 方法计算天然气偏差因子的误差分布提供了可靠的保证。

图2 原DAK 法计算天然气偏差因子误差分布Fig.2 Error distribution of Z-factor calculated with the original DAK method

应用上述6 548 组数据对DAK 法计算的天然气偏差因子数值的相对误差进行评价(图2)。由图2 可以看出，在常压条件下(pr≤15.0)，相对误差一般在1%以内。但是，当pr＞15.0 以后，近一半的范围相对误差大于1%。通过对相对误差进行分析，DAK 方法仍有进一步提高计算精度的空间。

为了重新确定式(1)中的系数值，所有的样本点对式(6)求解最优化问题，即:

应用6 548 组Standing-Katz 图版数据根据式(10)对式(6)进行最优化分析，得到修正的DAK模型系数为:

3 方法对比

为了说明本文修正的DAK 法计算天然气偏差因子的可靠性，将修正的DAK 法与原DAK 法计算结果的误差分布进行对比。

应用修正的DAK 方法计算天然气偏差因子，并计算对应的相对误差，将得到的相对误差在等压线和等温线构成的二维平面上作出等值线图(图3)。显而易见，修正后的方法与原方法相比，相对误差大于1%的区域(图中阴影部分)明显减小。同时，对6 548 组计算结果的分析可得，原DAK 法相对误差大于10%的数据样本有22 个，分布在1.05≤Tr≤1.10 和1.15≤pr≤1.95 的范围内。而笔者提出方法相对误差大于10%的数据样本仅有13 个，减少接近一半，全部分布在Tr=1.05 时(1.05≤pr≤1.60)和Tr=1.10 时(1.55≤pr≤1.90)的很小范围内，相对误差超高的样本数明显减少。

图3 修正的DAK 法计算天然气偏差因子误差分布Fig.3 Error distribution of Z-factor calculated with the modified DAK method

4 结束语

基于最优化方法对计算天然气偏差因子的DAK 法进行了修正，从而有效改善了天然气偏差因子的计算精度。在所分析的样本数中，相对误差大于1% 的比例由原来的大约10% 减小为3.5%。

［1］Katz D L，Cornell D，Vary J A，et al. Handbook of natural gas engineering［M］. New York:McGraw-Hill Book Company Incorporated，1959 :94-188.

［2］Smith R V.Practical natural gas engineering(Ed.2)［M］. Oklahoma:PennWell Publishing Company，1990:14-20.

［3］Bradley H B.Petroleum engineering handbook［M］.Richardson:Society of Petroleum Engineers，1987.

［4］Lee J，Wattenbarger R A.Gas reservoir engineering［M］.Richardson:Society of Petroleum Engineers，1996:16.

［5］Azizi N，Behbahani R，Isazadeh M A. An efficient correlation for calculating compressibility factor of natural gases［J］.Journal of Natural Gas Chemistry，2010，19(6):642-645.

［6］Gray E H，Sims H L.z-factor determination in a digital computer［J］.Oil and Gas Journal，1959，57(27):80-81.

［7］Hankinson R W，Thomas L K，Phillips K A.Predict natural gas properties［J］. Hydrocarbon Processing，1969，48(4):106-108.

［8］Yarborough L，Hall K R.How to solve equation of state for ZFactors［J］.Oil and Gas Journal，1974，72(7):86-88.

［9］Dranchuk P M，Purvis R A，Robinson D B. Computer calculations of natural gas compressibility factors using the standing and katz correlation［R］. Paper Petsoc 73-112 presented at the Canada Petroleum Society’s 24thAnnual Technical Meeting，Edmonton，1973.

［10］Dranchuk P M，Abou-Kassem J H.Calculations of z factors for natural gases using equations of state［J］.Journal Canadian Petroleum，1975，14(3):34-36.

［11］Alireza B，Saeid M，BrianF T. Rapidly Estimating Natural Gas Compressibility Factor［J］. Journal of Natural Gas Chemistry，2007，16(4):349-353.

［12］Ehsan H，Amir S，Jamshid M.A novel correlation approach for prediction of natural gas compressibility factor［J］. Journal of Natural Gas Chemistry，2010，19(2):189-192.

［13］Hall K R，Iglesias-Silva G A.Improved equations for the standing-Katz tables［J］. Hydrocarbon Processing，2007，86(4):107-110.

［14］Ehsan H，Jamshid M，Masoud R. New correlations to predict natural gas viscosity and compressibility factor［J］. Journal of Petroleum Science and Engineering，2010，73(1):67-72.

［15］李相方，刚涛，庄湘琦，等. 高压天然气偏差系数的高精度解析模型［J］.中国石油大学学报(自然科学版)，2001，25(6):45-46.Li Xiangfang，Gang Tao，Zhuang Xiangqi，et al.A analytic model with high precision for calculating compressibility factor of high pressure gas［J］. Jouranl of China University of Petroleum，2001，25(6):45-46.

［16］张明禄，胡建国，屈雪峰.应用状态方程计算天然气偏差因子的方法评价［J］.天然气工业，2003，23(2):69-71.Zhang Minglu，Hu Jianguo，Qu Xuefeng. Evaluating the methods of calculating gas deviation factor by use of state equation［J］.Natural Gas Industry，2003，23(2):69-71.