基于效率规则的混合作业车间调度算法应用研究
2013-12-23吴正佳祝小琴罗月胜
吴正佳 林 攀 张 成 祝小琴 罗月胜
(三峡大学机械与材料学院,湖北宜昌 443002)
在混合作业车间调度问题中,其中一部分工序是没有严格的先后顺序的;另一部分工序又具有严格的顺序,也就是说会有一些工序具有一个或多个紧前或紧后工序[1].混合作业调度问题具有作业方式多样化、规模庞大、系统复杂等特点.应用传统的函数分析方法,又很难将所研究的问题抽象为相应的数学问题,且计算量极其庞大,步骤过程也较为繁琐,故难以顺利完成[2].
本文设计了基于效率函数初排排序再调节排序的方法,来解决混合作业车间调度,并将该方法应用到具体的实例.结果表明这种基于效率规则的调度方法可以有效地优化混合作业车间最大完工时间,从而可以推广运用到混合车间调度问题的求解.
1 混合作业车间调度问题
1.1 问题描述
假设有m 台机器M1,M2,…,Mm需要加工n 个工件J1,J2,…,Jn.混合作业车间需要解决的两个关键问题:一是如何安排工序的顺序;二是如何确定工序在机器上的加工时间,并保持每个加工工件的工艺约束.和传统的车间作业调度问题相似,对此类混合作业车间调度问题也存在以下假设:1)一个工件同一时间只能在一台机器上加工;2)正在加工的工序不允许中断;3)同一时间一台机器只允许加工一个工件;4)每道工序只允许在一台机器上完成;5)工件在工序间可以等待,工件未到达前机器可以闲置;6)工件与机器的相关参数均一致,包括:工序在机器上的加工时间,工件的工艺路线;7)每个工件的第一道工序开始加工时间大于等于零[3-5].
1.2 问题数学建模

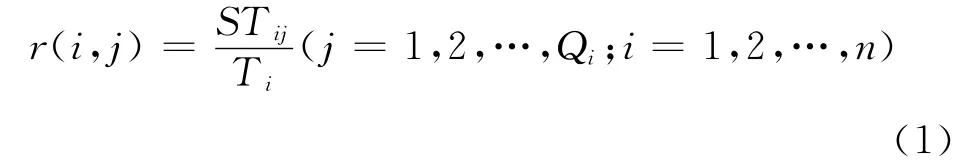
对加工效率r(i,j)作如下解释:假设r(i′,j′)是工件Ji′在加工工序Ji′i′时的加工“效率”,r(i″,j″)是工件Ji″在加工工序Ji″,i″时的加工“效率”,(1<i′,i′<n;1<j′<Q1,1<j″<Q2).若r(i′,j′)<r(i″,j″),则表明工件Ji′在加工工序Ji′i′时,其“效率”比工件Ji″在加工工序Ji″i″的“效率”低.

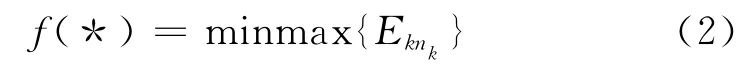
2 基于效率规则的混合作业调度算法设计
2.1 建立队列
对混合作业调度建立了3个队列:
工件队列.按其次序约束,出现多道紧前工序时,任意初始顺序,将每个工件的加工工序排列成队列LJi(i=1,2,…,n)[6].在此队列中,每个工序的加工时间不能重叠,即工件的前一道工序加工完成后才能进行后一道工序的加工.
机器队列.按实际加工顺序,将每台机器上加工的工件排列成队列LMk(k=1,2,…,m).在此队列中,每个工序的加工时间互不重叠,即工件在同一台机器上,当一个加工任务完成之后才能开始另一个加工任务[7].
工序多道紧前和紧后工序队列.建立工件每道工序的紧前队列LJibs(s=Ok,b=Qi,i=1,2,…,n),b代表某个工件的第几道工序,s表示工序b 的紧前工序的个数[8].因此,计算各工序的实际开工时间与完工时间时,必须保证3个队列的完整性.即调度问题就变成如何根据队列LJibs和LJi来确定工件队列的最终顺序,然后把LJi中的各工序如何插入到LMk中,并且保证目标函数值最优或近似最优.
2.2 初始化
1)工件队列:按照工件的每一道工序的次序约束,出现多道紧前工序时,初始顺序任意,建立各个工件的一个工件队列LJi(i=1,2,…,n).
2)根据式(1)计算每道工序的r(i,j),则对于各个工件Ji(i=1,2,…,n)满足max(1-r(i,j))的工序必在队首,出现多道紧前工序时都按照先加工计算效率.
3)机器队列:初始时各机器都未被分配,即每个机器队列LMk(k=1,2,…,m)均置空Null,而且每个机器Mk加工的工件数nk均置0,Mk0也置0.
4)建立多道紧前工序队列:依据各个工件的每道工序的紧前工序个数,建立各个工件的一个紧前工序队列LJibs(s=Ok,b=Qi,i=1,2,…,n)[9-10].
2.3 初排算法的设计
混合作业车间初排算法流程如下:
Step1:nk=0(k=1,2,…,m),W ={Jij|j=1,2,…,Qi;k=1,2,…,i=1,2,…,n};

Step3:在各个工序中选择满足加工效率值为max(1-r(i,j))(j=1,2,…,Qi;i=1,2,…,n)的工序Jij.如果不唯一,则取满足max{Ti-TSie}的工序Jij.然后循环到下一道工序Jij+1;
Step4:如果Pij=Mk,则将工序Jij插入到机器列队LMk的队尾;
Step5:分别依据式(3)、(4)和(5)计算工序Jij的开始时间STij、结束时间FTij和等待时间WTij;
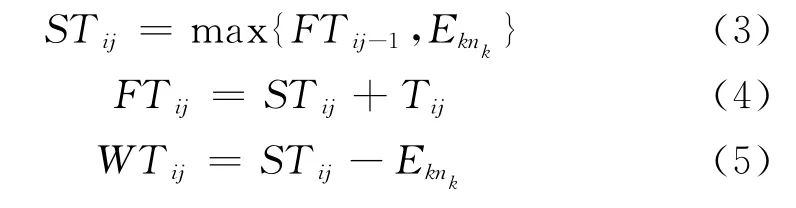
Step6:更新nk=nk+1,并Eknk=FTij;
Step7:判断工件队列LJi(i=1,2,…,n)是否遍历完毕,是则跳转Step8,否则,跳转Step3;

Step9:判断紧前工序队列数值是否全部为1,是则算法结束,否则,跳转Step2.
2.4 调节算法的设计
设Wkl为第K 台机器完成第L-1次加工Jij后要进行第l 次加工Ji′j′的等待时间,即:Wkl=WTi′j′(k=1,2,…,n;l=1,2,…nk),则
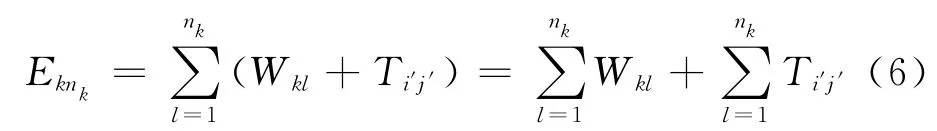

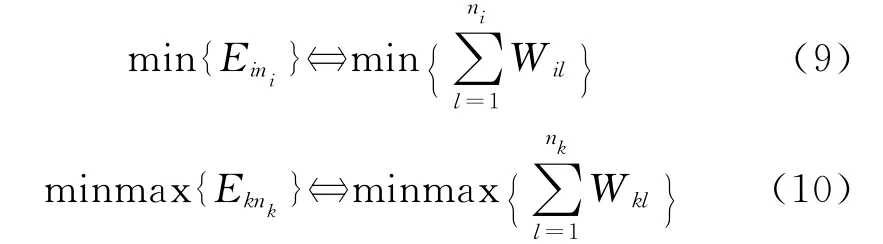
调节算法的目标为

具体调节算法流程为:
Step1:计算Wkl(k=1,2,…,m;l=1,2,…,nk);
Step3:遍历机器队列中LMk(k=1,2,…,m)对任意一个i,若Wil=0(l=1,2,…,ni)则排序结果最优,不需调节.此时,关键路径上的各个工序均无等待时间,排序结果最优,跳转Step9;
Step4:求wij={Wij},但wil≠0的工序Jpq;
Step5:设计器Mi上第j 次加工的工序为Jpq,j+1次加工的工序为Jp′q′,如果工序Jp′q′的前一道工序Jp′q′-1的结间束时FTp′q′-1<STpq,则交换Jp′q′和Jpq在机器Mi上的加工顺序;

Step9:算法结束.
3 实例计算与分析
某车间有4个工件在4台机床上加工,每个工件有4道工序,假定每个工件在每台机床上各加工一次,并且每道工序的加工时间和每个工件的加工路线已知,详细数据见以下3个矩阵:

运用上文中效率规则算法,对实例问题进行计算求解,并在开发的调度系统中以甘特图的形式进行调度结果输出,初排算法计算后输出结果和调节算法输出结果分别如图1~2 所示.图中,纵轴表示机器编号,横轴表示时间.

图1 初排结果输出界面

图2 调节结果输出界面
通过以上调度甘特图可以看出,进行初排算法计算后最长时间为17个工作时,再采用调节算法计算最终的调度结果为16个工作时.通过初排算法计算再调节计算后,整批工件的排产时间得到了很好的优化.证明了这种基于效率规则的调度算法可以很好地解决混合作业车间的调度问题,可以很好地应用于混合作业车间调度.
4 结 语
基于效率规则的混合车间调度算法,基本思想是在工件效率函数的基础上,设计初排排序再调节排序,最终得出调度结果.这种算法在混合作业车间调度问题中研究得比较少,可能还存在进一步的改进可能,但可以作为混合作业车间调度问题的一个新的研究方向,开展相应有意义的研究工作.
[1] Amit Kumar Gupta,Appa Iyer Sivakulllar.Job Shop Scheduling Techniques in Semiconductor Manufacturing[J].Int J Adv Manuf Technol,2006,27:1163-1169.
[2] 胡雅丽,杨建军.基于约束规则的作业车间调度研究[J].工业控制计算机,2012,48(5):43-46.
[3] Ling Wang,Da-Zhong Zheng.A Modified Evolutionary Programming for Row Shop Scheduling[J].Int J Adv Manuf Technol,2003,22:522-527.
[4] 曾利军,易理威,刘玲华,等.求解车间调度问题的离散粒子群优化算法[J].电脑知识与技术,2012,38(28):6787-6789.
[5] Tai,Tsu Ta,Boucher,Thomas O.An Architecture for Scheduling and Control in Flexible Manufacturing Systems Using Distributed Objects[J].IEEE Transactions on Robotics and Automation,2002,18(4):45-49.
[6] 王 冰,李巧云,羊晓飞.模糊车间作业调度的三点满意度模型[J].控制与决策,2012,27(7):1082-1086.
[8] 张 博.流水车间成组作业调度的仿真研究[D].天津:天津工业大学,2008.
[9] 崔雪丽.基于混合遗传算法的车间生产计划调度[J].计算机工程与设计,2011,36(7):25-29.
[10]Laguna M,Barnes J W,Glover F W.Intelligent Scheduling with Tabu Search:an Application to Jobs With Linear Delay Penalties and Sequence-dePendent Set up Cost and Times[J].Applied Intelligence,2003,56(3):159.
