基于灰色-模糊马尔可夫链模型的滑坡变形预测
2013-12-23朱惠群陈洪凯
朱惠群 陈洪凯
(重庆交通大学岩土工程研究所,重庆 400074)
滑坡的演变对人类的生活生产活动有着巨大的影响,准确地预报滑坡系统的演变具有重要的现实意义.而滑坡系统是一个受地质条件、地下水以及人类工程活动等多种因素影响的非线性动力系统,其演变规律极为复杂,表现出的力学参数及力学现象带有明显的不确定性和随机性.滑坡位移变形的分析也成了工程技术难题之一[1-3].
灰色理论由邓聚龙教授[4]提出,常见的GM(1,1)模型被广泛地应用到社会、工业、地质等众多学科.但是单一的GM(1,1)模型对于滑坡位移预测具有较大的误差,无法达到预测精度要求.各方学者也曾提出许多修正方法[5-7].本文在误差修正方面运用模糊数学思维,提出采用GM(1,1)-Fuzzy-Markov模型对相对误差进行二次预测,相比单一GM(1,1)模型预测的精度得到提升,效果显著.
1 GM(1,1)-fuzzy-Markov模型
1.1 滑坡变形的GM(1,1)预测


其中
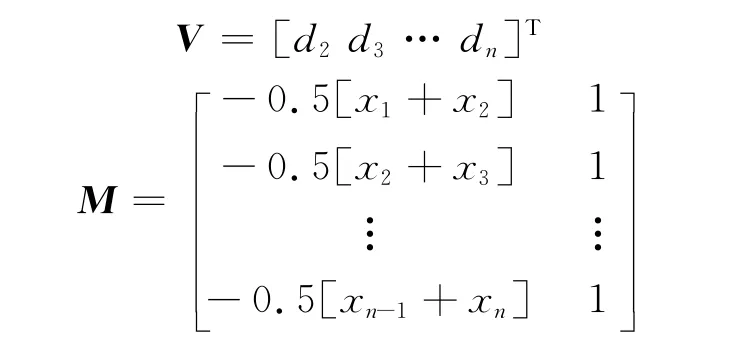


经过累减还原得到{dt}的预测模型
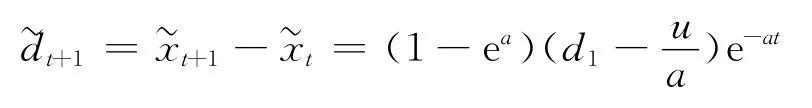
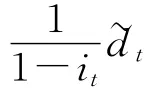
1.2 相对误差的Fuzzy-Markov模型
传统的Markov模型[8-10]只能将元素划分入明确的子集合,而这对于边界不明确的相对误差it过于绝对化,运用模糊理论将元素和集合之间用隶属度的方式拓广到[0,1][11-13].根据这个思想首先对相对误差k进行模糊状态的划分.划分出的k 个模糊状态E1,E2,…,Ek其隶属函数需要满足:
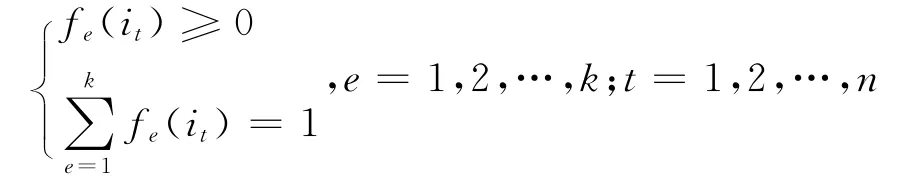
由此得到模糊状态矩阵E

设系统经过了m 步状态转移,则转移概率可作如下定义:

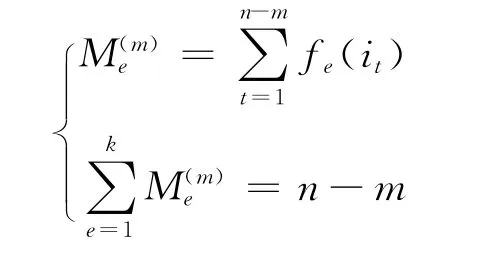
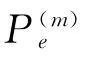

由状态Me经m 步转移到状态Mj的转移频数为

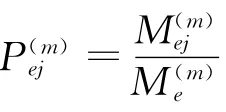
设第t个时间的状态向量为It
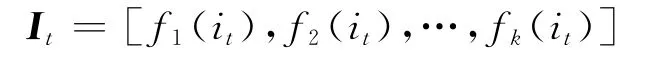
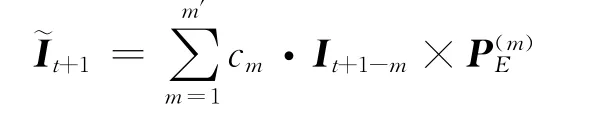
其中m′为采用几步转移步数累加预测,一般取5,cm为第m 步的转移权重.cm可由各阶自相关系数rm规范化得到,即

2 实例分析
本文以重庆云阳凉水井滑坡监测为例,进行短期预报分析.凉水井滑坡为推移式的深层大型、复活型土质老滑坡,位于云阳县水让村8组长江右岸斜坡地带,滑坡整体平面形态呈“U”形,后部地形呈近似圈椅状,南高北低,中后部地形较陡,前部地形较缓,自然坡度30~35°.凉水井滑坡滑体(Q4del)为滑坡堆积,主要由含角砾粉质粘土、人工填土、含碎石、块石粘土以及砂、泥岩块石组成;滑床为侏罗纪中统沙溪庙组(J2s)互层砂岩、泥岩;滑动带为滑坡堆积与下伏基岩接触带,滑动方向与现坡向基本一致.
图1为一监测点2009年4月6日~2009年5月8日的监测数据,共33组数据.假设最后4组数据未知,使用前29组数据计算GM(1,1)模型,得到GM(1,1)预测公式:


图1 凉水井滑坡一监测点实测曲线
根据上述的GM(1,1)预测公式,可以得到33组预测位移~dt+1,t=1,2,…,33,由于灰色预测头部具有较大的波动略去前4组数据,并计算从第5组开始到第33组的相对误差序列it,t=5,6,…,33.运用it的前25组数据进行Markov和fuzzy-Markov对最后4组数据进行滚动预测.
对it,t=5,6,…,29进行模糊状态划分,介于it多数元素取值区间为(-10%,10%),选取-10%,-5%,0,5%,10%这5个边界点,构造如下隶属函数:


隶属函数分布如图2所示.
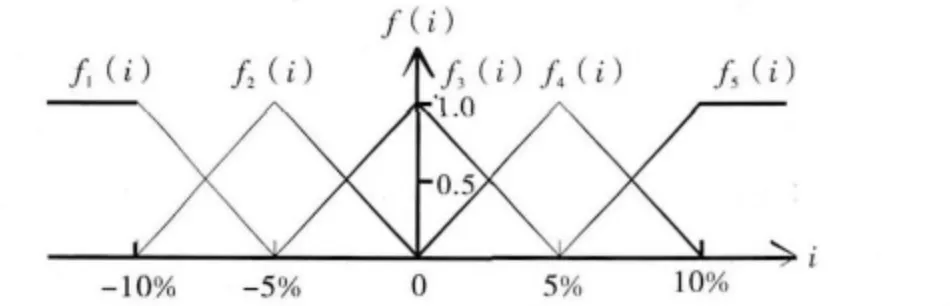
图2 模糊隶属函数分布图
取m′=5计算P(m)E,通过累积加权概率分别得到第30~33组的状态预测向量~It+1,选取最大可能性区间的中值作为i值的修正值.对i值修正后与单一的GM(1,1)模型进行对比,观察误差是否得到缩小及精度提高效果.
运用GM(1,1)-Markov模型计算出的修正后i值一同列入表1中进行对比.在对比关于i的Markov模型状态等分4 组与等分5 组后,表中给出结果相对要好的等分5 组预测后的修正i值参与对比.fuzzy-Markov预测结果均属于第二状态与实际相符,根据E2的上限和下限分别为0和-10%,给出了经过预测中值-5%修正后的相对误差,其相对单一的GM(1,1)模型有较大的精度提升,得到令人满意的预测效果,比传统Markov预测效果更好.
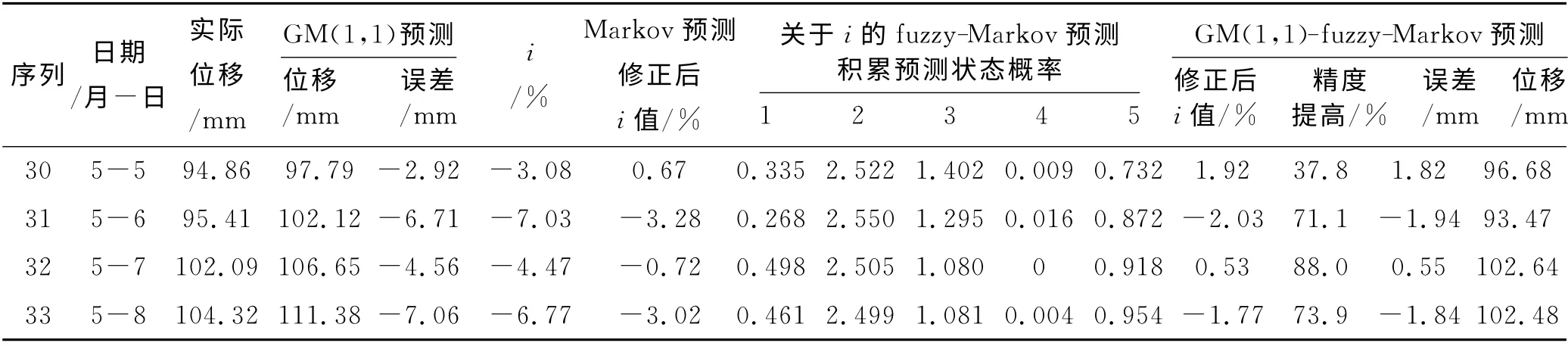
表1 位移预测对比成果表
3 结 论
1)本文提出滑坡变形的GM(1,1)-fuzzy-Markov模型,并通过实际算例验证了该模型在滑坡变形预测方面的可行性与适用性,为滑坡变形预测问题的解决提供了有益的思考与探索.
2)通过引入fuzzy-Markov理论,在一定程度上避免单一GM(1,1)理论无法预测波动性的局限,实现较好的预测,同时提高了预测精度.
3)与GM(1,1)-Markov模型对比说明了,在模糊状态划分下的Markov模型能更好地利用数据信息,避免硬划分造成的信息丢失,带来更佳的预测效果.
[1] 杨永波,刘明贵.滑坡预测预报的研究现状与发展[J].土工基础,2005,19(2):61-65.
[2] 王念秦,王永锋,罗东海,等.中国滑坡预测预报研究综述[J].地质论评,2008,54(3):355-361.
[3] 佘小年,傅鹤林,罗强等.公路滑坡崩塌地质灾害预测与控制技术[M].北京:人民交通出版社,2010.
[4] 邓聚龙.灰色系统理论教程[M].武汉:华中理工大学出版社,1992.
[5] 吴益平,滕伟福,李亚伟.灰色-神经网络模型在滑坡变形预测中的应用[J].岩石力学与工程学报,2007,26(3):632-636.
[6] 刘造保,石 雄.基于修正GM(1,1)模型的岩体边坡预测分析[J].三峡大学学报:自然科学版,2008,30(5):33-36.
[7] 王朝阳,许 强,范宣梅,等.灰色新陈代谢GM(1,1)模型在滑坡变形预测中的应用[J].水文地质工程地质,2009(2):108-111.
[8] 胡迪鹤.随机环境中马尔可夫过程[M].北京:高等教育出社,2011.
[9] 张 超,贾凤亭.Markov链的组合预测及其应用[J].辽宁工程技术大学学报:自然科学版,2011,30(6):963-966.
[10]徐 飞,徐卫亚.基于支持向量机-马尔可夫链的位移时间预测[J].岩土力学,2010,31(3):944-948.
[11]梁桂兰,徐卫亚.模糊马尔科夫链状模型在斜坡稳定性预测中的应用[J].中国地质灾害与防治学报,2006,17(4):64-67.
[12]刘 晓,唐辉明,刘 瑜.基于集对分析和模糊马尔可夫链的滑坡变形预测新方法研究[J].岩土力学,2009,30(11):3399-3405.
[13]赵琳琳,夏乐天.模糊加权马尔可夫链模型及其应用[J].江西农业学报,2007,19(1):151-153.
