流域分布式水文模拟中的模型网格尺度效应

罗智锋 王 文 陈 喜

（1.河海大学水文水资源与水利工程科学国家重点实验室，南京 210098；2.河海大学水文水资源学院，南京 210098）

水文尺度问题自20世纪90年代初被正式提出后，就受到广泛关注和重视.水文科学的理论研究与实践证明，不同尺度的水文循环机理有很大差异，如何考虑流域水文过程的时空不均匀性是尺度问题的关键［1］.从空间上来说，影响这种不均匀性的主要因素有流域地形、土壤、植被等数据质量.不同来源、不同网格分辨率的数据对流域特征描述的不一致，直接影响着模型的模拟精度.以往的研究表明，植被土壤数据的分辨率选择对水文模拟影响较小［2］，多数研究集中于分析DEM 网格水平分辨率的影响.DEM 是描述地表形状的连续变化的数据源，用于提取坡度、坡向、汇流路径长、集水面积、流域边界等流域特征.DEM 网格分辨率深深影响着以地形为基础的分布式水文模型.一些研究利用不同水平分辨率的DEM 提取地形特征，发现低分辨率导致平均坡度减小，流域面积和地形指数增加［3－4］.不少研究者分析了Topmodel的尺度效应，发现其对网格分辨率变化非常敏感［4－5］，网格大小的增大，导致平均地形指数相应增大，地下水埋深相应增加，模拟洪峰流量增加.另外一些研究也分析了不同网格尺度下的参数率定问题，如Molnar［6］通过比较分布式水文模型CASC2D 模拟结果对不同DEM 分辨率的敏感性，发现粗网格分辨率也可以进行水文模拟，但是要减小网格大小的影响，需要调整坡地汇流与河道糙率相关的参数.

另一方面，水文模型的结构具有尺度依赖性，随意选择网格大小影响着因模型结构原因带来的计算误差.例如，MIKESHE 和LISEM 模型网格尺度效应研究都发现，模型运动波求解时会产生数值误差，这种误差使洪水波发生扩散作用，且随网格增大而加强，从而导致洪峰模拟随着网格增大而减小［7－8］.

网格尺度从这两方面影响着模拟效果.因此，了解网格尺度变化对水文模拟的影响，对于提高模拟精度具有重要意义.本文通过多尺度试验，分析DHSVM 模型在不同尺度下的不同径流过程的响应特征，寻求合适的模拟尺度，为模型应用提供参考依据.

1 研究区域与数据

选择美国中部的伊利诺伊流域为研究流域，该流域位于阿肯色斯与俄克拉马州的边界（见图1），曾被选为分布式水文模型比较计划（DMIP）流域之一.流域气候为大陆性湿润气候，处于冷暖气流交替出现的地区，年平均最大、最小气温分别为22℃、9℃.多年平均降水为1 200mm，多年平均水面蒸发为1 066 mm，40%的降水发生于3～6月，接下来的夏季为干季，9～11月为湿季，30%的降水发生在此阶段，冬季流域为干旱季节.流域出口为Tahlequah站，实际控制面积为2 483km2，多年平均流量为29m3／s，月平均最高流量发生在3～6月，最低流量发生于7～8月，基流占年平均流量的29.7%～72.5%（1936～2007）.

流域内有6个气象站（如图1所示），提供逐小时气温、长短波辐射、水汽压、风速、降水等气象数据.植被分类数据来自国际地圈生物圈计划（IGBP）的1km分辨率数据库，土壤分类数据来自美国农业部（USDA）全国土壤测量中心的STATSGO 数据库，流域主要的植被类型是落叶阔叶林（91.8%），主要的土壤类型为粉质壤土（46.6%），其次是粉质黏壤土（38.1%）.其他数据包括流域DEM 数据（30m×30m）、植被覆盖度、水面蒸发、流量、河道断面等数据，大部分由NOAA 水文办公室DMIP网站提供.

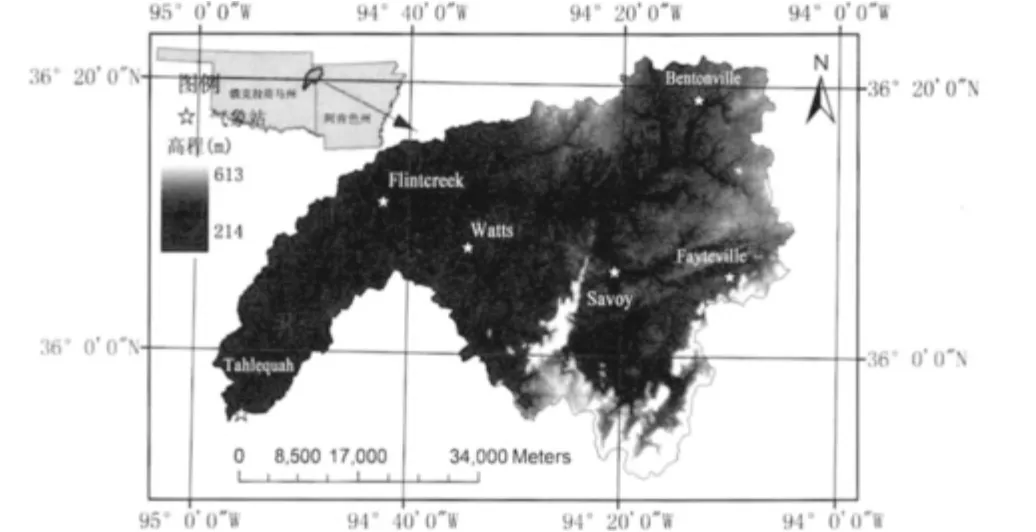
图1 伊利诺伊流域位置图

2 研究方法

2.1 模型简介

DHSVM（Distributed Hydrology Soils and Vegetation Model）模型由Mark Wigmosta于1994年提出［9］，用于模拟中小尺度流域（通常小于10 000km2）内土壤、植被和地形对地表以及地表以下水流运动的影响，目前最新的版本为DHSVM 3.0，为本研究采用版本.模型由7个模块组成：蒸散发、地面降雪和融雪、冠层截雪和积雪融化、不饱和土壤水运动、饱和壤中流、饱和坡面流和河道流量演算.模型采用基于Penman－Monteith公式的双层的树冠计算截留和蒸散发，采用质量、能量平衡模型计算积融雪，水分的垂向运动采用一维的达西流公式，计算经过多层土壤的不饱和壤中流.

DHSVM 采用近似运动波的方法逐网格计算壤中流，网格内水流可以向周围相邻8个方向网格（0～7）流动.网格（i，j）在k 方向上的饱和壤中流的输移率为：

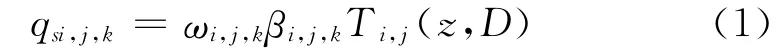
式中，ωi，j，k是k 方向上网格流线密度；βi，j，k是k 方向上地下水位线的坡度；Ti，j（z，D）是网格输移率.式（1）中的输移率的计算公式如下：

式中，Ki，j是网格表层土壤侧向饱和水力传导率；fi，j是垂向衰减系数；Di，j是网格土壤层厚度；zi，j是地下水位埋深；网格单元饱和壤中流的总出流等于式（1）计算的各方向的出流量之和.

模型坡面汇流也采用类似饱和壤中流计算的逐网格方法，并同时考虑了霍顿超渗产流、蓄满产流与回归流3种地面径流.与壤中流计算不同的是坡面汇流中的流速采用的是定值，等于网格大小除以时间步长，意味着一个时间步长内流出此网格的水量等于初始时刻的网格的储水量.

模型河道的流量演算采用相对简单但是很稳健的线性槽蓄法，改进的马斯京根法也可用于河道演算.线性槽蓄法对于大小不一、地形多变的流域，都能得到比较满意的模拟结果，在DHSVM 的应用中，大部分的河道汇流演算均采用此方法.模型更多结构介绍可参考文献［9］.

2.2 模型构建与率定

DHSVM 模型构建需要处理大量数据，除了上述提到的地形、植被、土壤数据，还需要河网和土壤深度数据，可通过自带的处理程序生成.将栅格数据处理成统一的空间步长，时间序列数据处理成统一的时间步长，以此为驱动数据，构建模型.参考Wigmosta应用于一个相似大小流域的模拟效果［9］，并经过初步模拟结果比较，确定空间步长为200m、时间步长为3h以构建模型.选取1994～1997年作为模型的率定期，1998～1999年为验证期，对模型进行手动率定与验证.

参数率定参照Wigmosta应用DHSVM 模型的经验，选择最小植被气孔阻抗、饱和侧向传导系数和侧向传导率垂向递减指数3个最为敏感参数进行调整.其他植被土壤参数分别采用Land Data Assimilation System（LDA）提供的植被分类标准基本参数表与NOAA 水文办公室提供的全球5min土壤参数分类基准参数表设定.率定过程，首先调整对水量平衡影响较大的最小植被气孔阻抗，使总径流偏差最小，然后再调整对洪水峰型影响较大的侧向传导系数与垂向递减指数，使模拟径流过程尽量接近实测径流过程.模拟效果采用确定性系数DC、径流深相对误差BIAS指标进行评价，如下式：

对模型率定期和验证期的逐日平均径流量的实测值和模拟值进行对比验证，结果显示率定期的确定性系数为0.71，总径流偏差为－0.56%；验证期效率系数为0.79，总径流偏差为7.12%，如表1所示.从率定期和验证期的洪水过程线（图2a、2b）可以看出模型对洪峰的模拟不太满意，低估了洪峰值.从总体上来看，模型在该流域具有适用性.率定后的模型参数用于尺度效应研究.

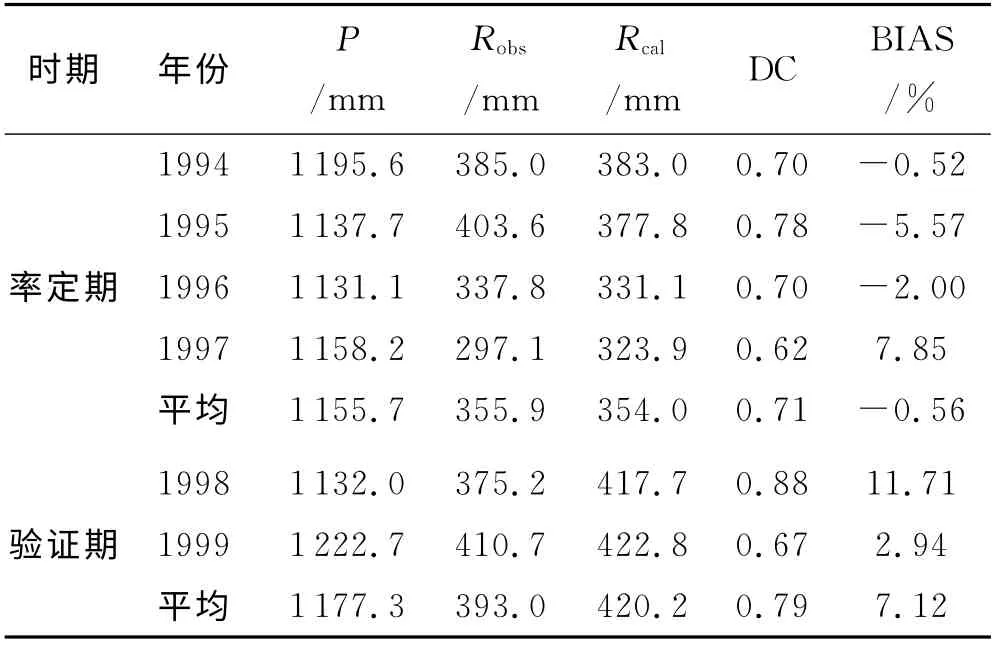
表1 模型率定期与验证期模拟结果

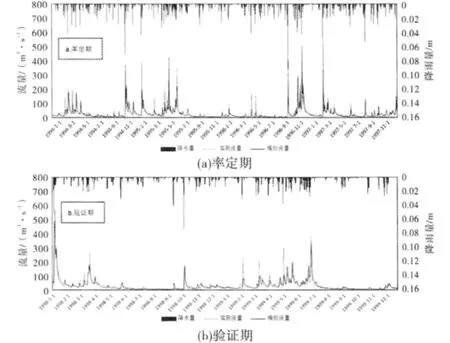
图2 模拟与实测流量比较

2.3 网格尺度效应模拟试验

本文采用两种方法来分析模型的网格尺度效应，一种是静态参数法，即保持率定好的参数不变，利用3种不同网格大小（100m×100m、200m×200m 和500m×500m）的DEM 提取流域特征，分别建立模型，分析空间模拟尺度变化对水文模拟的影响.另一种方法是变化参数法，选取模型最小植被气孔阻抗、侧向传导系数和侧向传导率垂向递减指数3个敏感参数，每次只改变其中一个参数，其他保持不变，分析不同参数对网格大小的敏感性.

3 模拟结果与分析

3.1 网格尺度对提取流域特征的影响

将原始30m×30m 分辨率DEM 通过ARCGIS最邻近插值方法分别重采样到100m、200m、500m，并提取流域特征，统计结果见表2.由表中可见随着网格大小的增加，DEM 高程各项（最大值、最小值、平均值与标准差）基本无变化，而坡度则随着网格大小增加而减小，说明大网格对流域描述会产生地形的坦化现象，地形特征的空间异质性变小.这与部分研究得到的结果相类似［2－4，10］，即不同网格大小的DEM 得出的流域面积、高程大体上一致，但对与流域坡度有关的参数的影响较大.

表2 不同DEM 分辨率提取的地形特征

3.2 网格尺度对流量模拟的影响

静态参数情况下，选取一场洪水（1997 年12 月31日06时～1998年1月16日21时），比较各网格下的模拟径流，发现随着网格的增大，模拟洪峰流量相应增大（如图3所示）.其中500m 分辨率对降水最为敏感，不仅洪峰大，峰现时间也相应提前.而从基流部分的模拟结果来看，随着网格的增大，基流流量呈减小趋势.

图3 不同网格尺度径流模拟结果

为进一步分析引起不同网格大小下模拟径流的差异的原因，将模型1997年12月31日～1998年1月16日降水、蒸发、不同产汇流成分统计见表3.

表3 不同网格尺度的产汇流模拟差异

从表3可见，随着网格大小的变化，降水、蒸发项影响均较小，径流深变化总体不大，但是径流成分有较大变化.网格分辨率越细，壤中流比例越大，其中100m 网格模拟的壤中流比例最大，达到了0.72.由此可知，网格大小影响着汇流过程中不同径流成分.不同网格尺度下汇入到河道的地表径流、壤中流模拟结果如图4所示.

图4 汇入到河道的地表径流、壤中流模拟结果比较

如2.1所述，DHSVM 模型计算坡面汇流采用定流速的计算方法，与平均坡度无关，而与网格大小和河网密度有关.为了消除河网密度对模拟结果的影响，生成河网时，各分辨率已采用相同的阈值，以保证河网密度相同.因此坡面汇流只与网格大小有关，即网格越小，地表径流要经过更多的网格，即更长的时间才能被河网截留.在一场洪水中，大网格由于汇流路径短，而降水往往是发生在有限的几个时间步长，因此有多部分的水量通过地表径流直接汇到河网［10］，引起地表径流增加.而对于壤中流采用的演算方法，每个时间步长流出网格各个方向的水量与局地坡度有关，另外还与侧向传导系数、递减系数有关.当设定同样的模型参数，壤中流汇流只与坡度有关.大网格引起地形坦化，平均坡度减小，壤中流出流缓慢，网格内更容易滞蓄水量.与小网格相比，壤中流出流较小，模拟的平均土壤含水量较大.

图5比较了1998年01月10日12：00（前期有降水，流域湿润）各分辨率下模拟的地下水位埋深空间分布情况.由图可见，随着网格的增大，流域内地下水位埋深普遍变浅，验证了网格大小对流域土壤水分空间分布影响较大.理论上，对于一场洪水的模拟，因为网格增大，导致地表径流增加，壤中流减小，这两种机制呈中和作用，但是从图4可以看出，洪水过程中，大网格的地表径流程陡涨陡落趋势，且占总径流的比例更大，从而容易产生峰现时间提前，峰值提高的洪水.

图5 不同网格模拟地下水埋深空间分布

比较本文与以往Topmodel模型网格尺度影响的研究结果发现，网格大小对两个模型模拟结果有相似的影响.对于Topmodel模型，随着分辨率的降低，流域平均坡度值偏小，计算的地形指数偏大，导致模拟洪峰流量增大，平均地下水埋深变小，地表径流占总径流比例增大［11］.模拟的土壤含水量空间分布也有类似的结果，大网格水量滞蓄导致更大的饱和面积［2］.从两者模型汇流模块的结构分析入手，可以发现其深层原因.DHSVM 模型的壤中流汇流方法又被称为显式汇流方法（Explicit Routing）［12］，与Topmodel采用的基于统计理论的隐式方法（Implicit Routing）在机理上有一定程度的相似性，它们都假设土壤侧向饱和水力传导率随土层深度呈指数递减关系，且基于类似运动波方法计算壤中流输移率.所不同的是Topmodel采用统计－动力方法计算流域土壤水的分布，简化了计算量，使模型运算效率比DHSVM 高，但又不失其物理基础.而DHSVM 模型采用逐网格方法将水流汇至流域出口，充分考虑了单元间的水流累积对径流模拟的影响，物理概念更明确.Tague和Band［12］在一个小流域上比较过两种汇流方法，发现两种方法都能达到较好的径流模拟效果，但隐式方法对土壤含水量的空间分布的模拟不如显式方法精确，而且隐式方法模拟径流量对地形数据的坦化和土壤传导系数的变化更为敏感.因此，两种相似的汇流方法在地形均化影响下，具有一致的网格尺度效应.值得注意的是，两者的地表径流计算方法并不相同，DHSVM 模型地表径流影响直接来源于网格尺度的选择，而Topmodel则来源于地形均化的影响.

3.3 网格大小对参数敏感性影响分析

为了分析网格大小对参数敏感性的影响，选择最小植被气孔阻抗、侧向传导系数和垂向递减指数3个参数，每次只改变一个参数值，其他参数保持前面率定好的不变，并假设改变的参数在空间上均匀分布，运行模型，统计1994～1999年各网格的模拟效果.

由图6可见，各网格大小下的参数敏感性不一致.从确定性系数来看，最小植被阻抗与垂向递减指数的敏感性在100m、200m 网格尺度下比较接近，500m 网格尺度下各参数敏感性比较大，且与其他网格尺度变化规律不一致.侧向传导系数的敏感性随着网格大小的增大而增大，说明网格大小对侧向传导率的敏感性影响较大.由此可见，侧向传导系数是尺度效应较大参数.而从水量误差来看，各网格下的参数敏感性比较接近，网格越大，模拟水量负偏越大.

图6 不同网格下的参数敏感性分析

Topmodel参数尺度效应分析研究发现，产汇流过程中重要的敏感参数饱和导水率T0与网格分辨率有关，网格增大后如要保证模型的精度保持稳定有效，必须给T0赋较大的值［3］.本研究中，500m 的网格尺度下要提高模拟精度，应增加侧向传导率的值.结合前面分析的汇流演算方法，当侧向传导系数增大时，壤中流更容易流出网格，水量滞蓄作用将减弱，一定程度减小了网格增大带来的尺度影响.但此时模型具有物理意义的参数可能会变成有效参数，在一定程度影响了模型的物理基础，故不推荐使用500m 的网格进行建模.

小网格在大流域的应用上受运算效率的限制，本研究流域为中等大小流域，100m 步长将流域划分成了606×840个网格，在一台配置为I3处理器／4G 内存的计算机上，模拟一年平均需要25min，而200m网格步长平均只需要5分钟，小网格明显增加了模型参数率定的难度.模型在200m 网格大小下的模拟效果表明此网格大小分辨率已经满足水文模拟的要求，同时又兼顾了模型运算效率.

4 讨论与结论

4.1 讨论

总而言之，本文揭示的尺度效应源于两方面，一是由于网格增大导致地形数据均化，均化后的坡度、河长等参数，输入到模型中，间接影响了模拟结果.另一方面的原因是模型结构具有尺度依赖性，使网格大小的选择对汇流过程产生直接影响.如前所述，分布式水文模型汇流，有不少采用运动波或扩散波方法的汇流模型，需要利用有限差分求解微分方程，网格离散大小的选择则不可避免地会对求解过程带来误差.DHSVM 模型汇流算法在一定程度避免了差分求解时网格离散带来的尺度效应，但地表径流汇流模块仍面临着尺度问题.已有相关的模型，如改进的TOPKAIPI模型，通过引进控制性方程的空间积分和参数的平均化处理，旨在减轻网格尺度效应的影响，模型在一个流域上应用于从几米到几千米的网格尺度，物理意义和模型的计算精度并未受影响［1］.DHSVM 开发初衷是应用于30～200m 的空间尺度和1～3h的时间尺度上，属于比较精细的分布式水文模型.以往应用中，考虑到模型模拟效果与运行效率，小流域（几十平方千米）一般采用30m 网格尺度，中等流域（几百平方千米至数千平方千米）则可以采用100～200 m 的网格尺度，而大于200m 的网格尺度应用较少［9，13］.在以后的应用研究中，应特别注意网格大小对模拟结果的影响，选择合适的模拟尺度.

4.2 结论

本文利用3种不同网格分辨率的DEM（100m、200m、500m）建模，分别通过静态参数法（即保持200 m 下率定好的参数不变）与等步长变化参数的方法进行多尺度模拟，分析了各个模拟尺度下的水文要素与模型参数的尺度效应，主要结论如下：

1）在静态参数条件下，发现网格大小对模拟蒸发量、总径流量影响较小，而对洪峰和径流过程的模拟影响较大.网格越大，洪峰峰值越大，地表径流占总径流比例越大，网格水量滞蓄作用增大.

2）用变化参数法分析网格大小对参数敏感性的影响，发现侧向传导系数的敏感性随着网格增大而增大，明显具有网格尺度效应.大网格要提高模拟效果，需要增加侧向传导率的值，但要特别注意参数的有效性.

3）水文模型只有应用于一定尺度范围内才会得到预期的模拟效果，本文对DHSVM 模型尺度适用性初步分析可见，模型网格划分时应充分考虑网格选择对不同水文过程内部机理的影响，本研究表明200 m 的分辨率已能达到较满意的模拟效果.

［1］ 徐宗学.水文模型［M］.北京：科学出版社，2009.

［2］ Kuo W L，Steenhuis T S，McCulloch C E，et al.Effect of Grid Size on Runoff and Soil Moisture for a Variable－Source－Area Hydrology Model［J］.Water resources research，1999，35（11）：3419－3428.

［3］ 孙立群，胡成，陈 刚.TOPMODEL 模型中的DEM尺度效应［J］.水科学进展，2008，19（5）：699－706.

［4］ Vieux B E.DEM Aggregation and Smoothing Effects on Surface Runoff Modeling［J］.Journal of Computing in Civil Engineering，1993，7（3）：310－338.

［5］ Zhang W，Montgomery D R.Digital Elevation Model Grid Size，landscape Representation［J］.Water resources research，1994，30（4）：1019－1028.

［6］ Molnar D，Julien P.Grid－size Effects on Surface Runoff Modeling［J］.Journal of Hydrologic Engineering，2000，5（1）：8－16.

［7］ Ali M，R S，Ali R，et al.Simulations of Varying Grid Sizes on Catchment Yield by Using Calibrated and Validated MIKE SHE Models［M］.18th World IMACS／MODSIM Congress.Cairns，Australia.2009.

［8］ Hessel R.Effects of Grid Cell Size and Time Step Length on Simulation Results of the Limburg Soil Erosion Model （LISEM）［J］.Hydrological Processes，2005，19（15）：3037－3049.

［9］ Wigmosta M S，Vail L W，Lettenmaier D P.A Distributed Hydrology－Vegetation Model for Complex Terrain［J］.Water resources research，1994，30（6）：1665－1680.

［10］Dubin A M.Assessing the Influence of Digital Elevation Model Resolution in Hydrologic Modeling［M］.University of Washington，1998.［11］Wolock D M，Price C V.Effects of Digital Elevation Model Map Scale and Data Resolution on a Topography－Based Watershed Model［J］.Water resources research，1994，30（11）：3041－3052.

［12］Tague C，Band L.Evaluating Explicit and Implicit Routing for Watershed Hydro－Ecological Models of Forest Hydrology at the Small Catchment Scale［J］.Hydrological Processes，2001，15（8）：1415－1439.

［13］Vanshaar J R，Haddeland I，Lettenmaier D P.Effects of Land－cover Changes on the Hydrological Response of Interior Columbia River Basin Forested Catchments［J］.Hydrological Processes，2002：2499－2520.