大跨度部分地锚斜拉桥力学分析与参数研究

肖汝诚 卫 璞 孙 斌

(同济大学桥梁工程系,上海200092)

斜拉桥跨径增长受到诸多因素制约,包括抗风稳定性,超长斜拉索的强度、刚度问题以及塔梁交界处过大的主梁轴力等[1].国内外学者针对上述问题提出了诸多解决方案[2-3],其中针对主梁轴力过大问题,Gimsing等[4]提出的部分地锚斜拉桥概念得到广泛的关注.如图1所示,部分地锚斜拉桥的部分锚索锚于锚碇,减小了主梁中的轴压力,并在跨中产生拉力,这一结构体系使主梁内的轴力分布更加均匀,并能提高结构刚度,为增加斜拉桥跨径提供了思路.

近年来,国内外学者对部分地锚斜拉桥进行了大量研究工作[5-10],然而研究手段大多局限于有限元分析方法,解析分析方法研究相对较少.与有限元分析方法相比,解析方法能更直观地反应设计参数对结构受力的影响,使工程师对于结构受力性能有更好的把握,并能在概念设计阶段提供简单有效的分析手段.此外,大跨度部分地锚斜拉桥暂无工程实例可供参考,基于解析公式的参数研究还可以为概念设计时的参数选择提供依据.

本文基于索面膜化假定,推导了部分地锚斜拉桥受力的解析计算公式,与有限元分析结果进行了对比,并以此为基础进行了边中跨比、塔梁高跨比、主梁刚度、索塔刚度和地锚锚索支承刚度等参数的分析研究,为该桥型的概念设计提供理论参考.

1 平衡微分方程及其近似解

1.1 基本假定

本文采用如下分析约定:

1) 现代斜拉桥多采用密索体系,为简化分析,将斜拉索面简化为连续的索膜.

2) 为提高拉索支承效率,斜拉桥以扇形索面居多,本文假定斜拉索锚固于索塔顶端,为理想扇形体系.

4) 主梁采用漂浮体系,纵向无约束.

此时结构位移可按下述位移量表示:主梁竖向位移v(x),梁端纵向位移w,左右索塔塔顶水平位移uL和uR,各位移量以图2中所示方向为正.

图2 部分地锚斜拉桥计算简图

1.2 平衡微分方程

以主梁为研究对象,在活载及索面的连续作用力下,其平衡微分方程为

EIvIV=p-qcV,p

(1)

式中,E,I分别为主梁的弹性模量和抗弯截面惯矩;qcV,p为活载引起的斜拉索竖向力集度.

以索塔为研究对象,左右索塔塔顶水平力平衡条件为

(2)

(3)

以主梁和索面整体作为研究对象,水平方向仅受到地锚索力和塔顶水平力,平衡方程为

fHLe,p+kuL=fHRe,p+kuR

(4)

假设每根斜拉索承担其索距范围内的恒活载,则单位长度上的拉索面积为

(5)

式中,As为斜拉索面积;λ为拉索间距;θ为斜拉索倾角.由式(3)和图3所示的位移变形关系求得单位长度斜拉索索力,并向竖直方向投影后可得

(6)

向水平方向投影后可得

(7)

(8)

式中,Es为斜拉索弹性模量;γ为斜拉索重度;l0为斜拉索的水平投影长度.

图3 位移分量引起的斜拉索变形示意图

令地锚锚索面积为Ase,仅塔顶水平位移引起其变形,假设地锚索锚固位置与梁平齐,由图3位移变形关系求得其索力,并向水平方向投影可得

(9)

(10)

令自锚锚索的面积为Asa,仅塔顶水平位移和主梁水平位移引起其变形,由图3位移变形关系求得其索力,并向水平方向投影可得

(11)

(12)

(13)

(14)

(15)

(16)

(17)

ξ=ξp+ξe

(18)

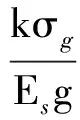
(19)

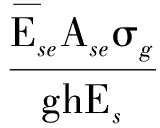
(20)

式中，X在左右扇面内分别为XL和XR.

1.3 平衡微分方程的近似解

微分方程组中,ε表示主梁抗弯刚度与斜拉索轴向刚度之比,对大跨径桥梁,ε为微小量[12],微分方程的近似解由2部分组成[13]:当ε=0时，特解为V0,U0,W0;当ε≠0时，通解为V1,U1,W1.其中,V0,U0,W0为忽略主梁刚度时的结构位移,此时活载全部由斜拉索承担,反应纯缆索体系刚度,其解为

(21)

(22)

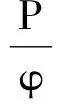
(23)

V1,U1,W1反应主梁抗弯刚度对结构响应的影响,其解为

U1=W1=0

(24)

V1=C1eg(X)sing(X)+C2e-g(X)sing(X)+

C3eg(X)cosg(X)+C4e-g(X)cosg(X)

(25)

(26)

2 关键力学响应计算及验证

2.1 关键力学响应计算公式

通过上述微分方程及其近似解,可计算部分地锚斜拉桥的下述关键力学响应:中跨最大挠度、弯矩;塔顶最大位移;自锚锚索最大应力、应力幅;地锚锚索最大应力、应力幅,对应的活载工况及计算公式如表1所示.

表1 关键力学响应计算公式

2.2 有限元验证

为验证上述计算公式精度,对一座部分地锚斜拉桥方案进行了分析.该桥跨径布置为430 m+1 300 m+430 m.主梁梁高4.5 m,面积A=2.116 m2,竖向抗弯惯矩I=7.396 m4.主塔全高为350 m,塔顶抗推刚度为9 295.9 kN/m.拉索强度设计值为710 MPa.活载按公路Ⅰ级取值.结构立面布置如图4所示.有限元模型采用单鱼骨梁模型,分别进行活载满布中跨、两边跨、半中跨和一边跨4种工况下的荷载效应计算.

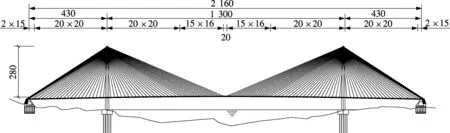
图4 部分地锚斜拉桥方案立面布置(单位：m)

图5为各关键响应计算值的相对误差,从中可以看出,本文计算与有限元计算结果相比,误差均在15%以内.其中跨中位移计算结果误差小于3%.

图5 各关键响应计算值的相对误差

计算误差来源主要包括简化分析中的膜化假设、理想扇形索面假定、未考虑大位移效应、垂度修正仅采用切线模量以及微分方程的解中忽略了ε的高阶项等.

3 参数研究

作为一种新型结构体系,部分地锚斜拉桥的概念设计无工程实例可供参考,其参数取值需要通过分析方法获得.本节对边中跨比、塔梁高跨比、主梁刚度、索塔刚度和地锚锚索支承刚度等参数对关键力学响应的影响进行分析,为该桥型的概念设计提供参考.分析中,活载集度取为50 kN/m,其余参数除待讨论参变量外,均与上节所述桥梁方案相同.

3.1 边中跨比

图6为部分地锚斜拉桥边中跨比对各关键力学响应的影响.可以看出：① 边中跨比对跨中挠度、弯矩、地锚锚索最大应力以及自锚锚索应力幅的影响均呈抛物线形状,在边中跨比接近0.3取得最小值;② 边中跨比增长会减小自锚锚索最大应力，当边中跨比由0.1增加到0.3时,自锚索最大应力降低148.2 MPa,而从0.3变化到0.6时,自锚锚索应力仅减小38.9 MPa;③ 边中跨比增长会导致地锚锚索应力幅增加,当边中跨比由0.1增加到0.3时,地锚锚索应力幅增加仅10.8 MPa,但从0.3增加到0.6时,地锚索应力幅增量达115.3 MPa.

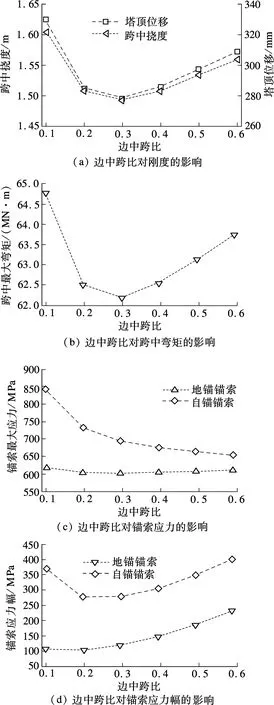
图6 部分地锚斜拉桥边中跨比对各关键力学响应的影响

以上分析可以看出,边中跨比取0.3左右,不仅可以使部分关键力学响应取得最小,而且对自锚锚索应力和地锚锚索应力幅的影响均相对较优.这一结果与文献[7]基于有限元的分析结果一致,其中，文献[7]的试设计边中跨比取值为0.317.

从数值来看,边中跨比对跨中弯矩的影响最小,对跨中挠度、塔顶位移和锚索应力的影响次之,而对锚索应力幅影响较大.这是由于锚索最小应力均对应边跨满载工况(见表1),在主跨一定的情况下,边跨跨度的增加会使最小应力减小,从而导致应力幅增长较快.

3.2 塔梁高跨比

图7为塔梁高跨比(桥面以上索塔高度与主跨跨度的比值)对各关键力学响应的影响.可以看出,除索塔塔顶位移外,塔梁高跨比的增加均可有效减小各力学响应.这是由于塔高增加,可以提高斜拉索的支承效率,但由于同时减小了自身线刚度以及地锚锚索支承刚度,因此增加至一定程度后会使塔顶位移有增加趋势.

图7 塔梁高跨比对各关键力学响应的影响

随着塔高的增加,曲线下降斜率均趋缓,表明塔高对力学响应的减小效果呈递减趋势.例如,当塔梁高跨比由0.1增加至0.2时,跨中弯矩减小27.077 5 MN·m,而从0.5增加至0.6时,弯矩仅减小5.593 5 MN·m.除此之外,塔高增加还会造成上下部结构造价和施工风险的增长.

基于上述分析,部分地锚斜拉桥的塔梁高跨比可按传统斜拉桥取值,其合理范围在1/4～1/7之间[14].

3.3 主梁刚度

图8为主梁刚度对跨中挠度和弯矩的影响.计算时所取主梁刚度为原始数值与图中所示主梁刚度系数的乘积.可以看出,随着主梁刚度的增长,跨中挠度减小而弯矩增加.从数值来看,当主梁刚度系数由0.2增加至2.2时,跨中挠度从1 574.2 mm减少至1 445.4 mm,变化幅度仅为8.18%,而跨中弯矩则由18.607 4 MN·m增加至112.388 6 MN·m,增幅达504%.可见,大跨度部分地锚斜拉桥结构刚度主要由缆索体系提供,主梁自身刚度贡献较小.增加主梁刚度不仅对结构整体刚度影响甚微,而且会急剧增加主梁自身承担弯矩.设计中,当结构强度无法满足要求时,应采用增加钢板厚度的方法进行调整,而避免采用增加梁高的措施.

图8 主梁刚度对跨中挠度和弯矩的影响

3.4 索塔刚度与地锚锚索支承刚度

图9为索塔刚度对跨中挠度和塔顶位移的影响.与自锚斜拉桥不同,地锚锚索对塔顶提供弹性支承,其刚度大小ξe对结构的影响是值得讨论的问题.图10为地锚锚索支承刚度对跨中挠度和塔顶位移的影响,计算时所取索塔和地锚锚索支承刚度为原始数值与图中所示刚度系数的乘积.

图9 索塔刚度的影响

图10 地锚锚索支承刚度的影响

当索塔刚度系数由0.2增加至2.2时,跨中挠度减小5.2%,塔顶位移减小12.7%;而当地锚锚索支承刚度系数由0.2增加至2.2时,跨中挠度减小42.4%,塔顶位移减小73.2%.可见,与传统自锚式斜拉桥不同,索塔刚度对结构整体刚度贡献较小,而地锚索对塔顶的弹性支承刚度对结构整体受力行为影响较大.

从式(20)可以看出,在地锚锚索面积、弹性模量和恒载应力一定的情况下,其支撑刚度主要取决于倾角大小,式(20)中与角度相关的参数为

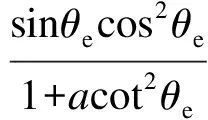
(27)

图11为角度参数与地锚锚索倾角的关系,从图中可以看出,为保证地锚锚索对塔顶的支承效率,其倾角在35°～50°之间最优.

图11 地锚锚索角度参数

4 结论

1) 大跨度部分地锚斜拉桥的边中跨比可取为0.3左右.

2) 塔梁高跨比取值可与传统斜拉桥相近,即取1/4～1/7.

3) 大跨度部分地锚斜拉桥主梁刚度对结构整体刚度影响很小,但对自身弯矩影响较大.

4) 地锚锚索支承刚度对结构整体受力影响远大于索塔自身刚度,为保证支承效率,地锚锚索倾角应在35°～50°范围内.

)

[1] 王伯惠. 斜拉桥的极限跨径 [J]. 公路, 2002 (4): 38-48.

Wang Bohui. Extreme span length of cable-stayed bridge [J].Highway, 2002(4): 38-48.(in Chinese)

[2] 王伯惠. 斜拉桥增大跨径的技术措施 [J]. 公路, 2003(2): 57-65.

Wang Bohui. Technical measures to enlarging span length of cable-stayed bridge [J].Highway, 2003(2): 57-65.(in Chinese)

[3] Starossek U. Cable-stayed bridge concept for longer spans [J].JournalofBridgeEngineering, 1996,1(3): 99-103.

[4] Gimsing N J, Georgakis C T.Cablesupportedbridges:conceptanddesign[M]. Chichester, UK: Wiley, 2012.

[5] Nagai M, Fujino Y, Yamaguchi H, et al. Feasibility of a 1 400 m span steel cable-stayed bridge [J].JournalofBridgeEngineering, 2004,9(5): 444-452.

[6] Won J H, Yoon J H. Structural effects of partially earth-anchored cable system on medium-span cable-stayed bridges [J].InternationalJournalofSteelStructures, 2008,8(3): 225-236.

[7] Sun Bin, Cheng Jin, Xiao Rucheng. Preliminary design and parametric study of a 1400m partially earth-anchored cable-stayed bridge [J].ScienceinChinaSeriesE:TechnologicalSciences, 2010,53(2): 502-511.

[8] Zhang Liwen, Xiao Rucheng, Xia Ruijie. Mechanical analysis and study on structural parameter of partially earth-anchored cable-stayed bridge part Ⅰ: mechanical analysis [J].AppliedMechanicsandMaterials, 2011,44-47: 1898-1905.

[9] Zhang Liwen, Xiao Rucheng, Xia Ruijie. Mechanical analysis and study on structural parameter of partially earth-anchored cable-stayed bridge part Ⅱ: parametric study [J].AppliedMechanicsandMaterials,2011,44-47: 1906-1912.

[10] Kim S H, Won J H, Cho K I, et al. Behavior of partially earth anchored cable-stayed bridge considering construction phase and operational phase [C]//IABSESymposiumReport. Weimar, Germany, 2007:1-8.

[11] 重庆交通科研设计院. JTG/T D65-01—2007公路斜拉桥设计细则 [S]. 北京:人民交通出版社,2007.

[12] Bruno D, Leonardi A. Natural periods of long-span cable-stayed bridges [J].JournalofBridgeEngineering,1997,2(3): 105-115.

[13] Bruno D, Grimaldi A. Nonlinear behavior of long-span cable-stayed bridges [J].Meccanica, 1985,20(4): 303-313.

[14] 邵旭东,胡建华. 桥梁设计百问 [M]. 北京: 人民交通出版社, 2003.