不同预应力度简支梁拉压杆模型
2013-12-23仲济涛
仲济涛 刘 钊
(东南大学混凝土及预应力混凝土结构教育部重点实验室, 南京 210096)
在混凝土梁桥的设计中,D区是指截面应变分布呈现明显非线性的区域.由于D区力流紊乱,平截面假定不再适用.拉压杆模型是D区设计的一种实用的新方法,是由德国Ritter和Mörsch提出的经典桁架模型逐渐演变而来,自20世纪80年代以来,经众多研究者[1-3]的探索,拉压杆模型已被广泛认为是指导配筋设计的有力工具[4-5].
确定拉压杆模型的构形是D区设计的第一步.在构形方法中,除荷载路径法和应力迹线法外,一些研究者提出利用拓扑优化方法进行构形.此方法按基本结构类型可分为2类:以微桁架作为基本结构[6-7]和以连续体作为基本结构[8-11].文献[8]将PBO方法(performance-based optimization)用于钢筋混凝土结构拉压杆模型的自动构形,并以带位移约束条件的结构重量作为结构性能指标.文献[10]研究了预应力混凝土梁拉压杆模型的构形方法,通过把预应力作为外荷载,将预应力混凝土拉压杆模型的构形问题转换为连续结构的拓扑优化问题.文献[12]提出了一种自动搜寻拉压杆模型最优构形的方法.文献[13]基于最小应变能准则提出一种自动构建拉压杆模型的一般化方法.文献[14]利用渐进结构优化(evolutionary structural optimization,ESO)方法构建了钢筋混凝土结构的拉压杆模型,此方法适用于平面应力单元以及与其等效的桁架单元.文献[15]利用拓扑优化和最小应变能准则构建了锚固横隔板的三维拉压杆模型.文献[9,11]借助有限单元库,提出一种基于最小柔度优化的方法构建拉压杆模型,并将此方法的应用扩展到多工况荷载下钢筋混凝土结构的抗震设计.
本文针对不同预应力度λ下的预应力混凝土简支梁,自行编制了单元生死并行的双向渐进结构优化程序,实现了拉压杆模型的自动构形.在此基础上研究了不同预应力度下预应力混凝土简支梁的受力行为,并与Schlaich等[1]构建的拉压杆模型进行了对比分析.
1 双向渐进结构优化方法
1.1 性能指标
根据ESO方法的原理,本文取下式作为结构进化的性能指标:

(1)
式中,E0,V0及Ei,Vi分别表示初始状态下及经过第i次优化后结构的总应变能和总体积.
1.2 应力约束
在结构中,每个单元对结构性能的贡献并不相同,这就需要优化算法对单元进行选择,删除对结构力学性能影响小的单元,保留或增加对力学性能影响大的单元.应力优化是结构优化最初的研究方向.Von Mises应力准则是常用的准则之一,即
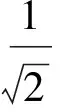
(2)
式中,σVM是单元的Mises应力;σ1,σ2,σ3分别表示第一主应力、第二主应力与第三主应力.
本文拓扑优化的基本思想是在高Mises应力单元周围生成新单元,共同分担应力以降低应力水平,同时删除低Mises应力单元,如图1所示.反复迭代,最终使得结构中的应力分布趋于均匀.为方便描述,作如下定义:
Ti+1=Ti+TiTi+1∈Γ;i=1,2,…,n
(3)
式中,Ti+1为第i+1阶拓扑构形;Ti为结构进化方向;Γ为进化空间;n为迭代次数.其中Ti的确定是优化的关键.本文参考文献[16]关于优化准则的理论,通过应力一致的原则确定Ti.

图1 单元生长与删除
双向渐进结构优化经常存在如下问题:若生长率过大,则会导致单元生长过剩,结构拓扑构形冗余单元较多;若删除率过大,则会导致结构拓扑构形变化较大,求解不易收敛.针对此缺陷,本文引入单元生长和删除加速度因子Fa,Fr,使得在优化初期,结构以生长为主,到达设置的迭代次数后,结构生长减缓,单元删除率逐渐增大,从而增强了双向渐进结构优化程序的稳定性.单元生长与删除的具体规则如下:在每次迭代过程中,若单元Mises应力满足下式:
(4)

(5)
式中,A为生长率基数,本文取0.95;Ia为生长进化速度,本文取0.002;Fa为生长加速度,其表达式为

(6)
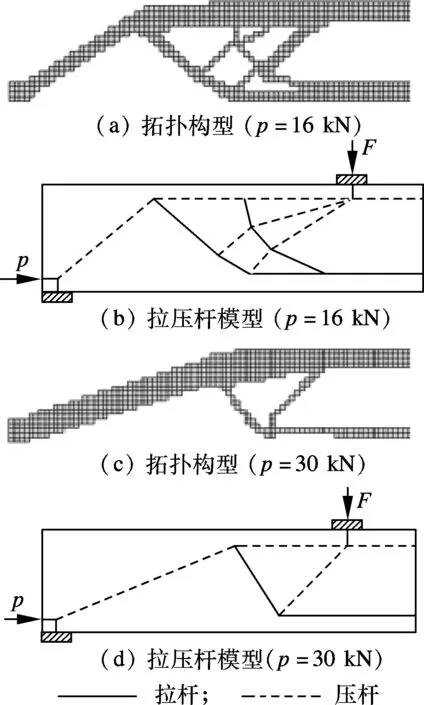
式中,i表示迭代次数;Ca为设置的生长加速点,Ca∈N,且Ca 若单元Mises应力满足下式: (7) Rr=D+(i-1)IrFr (8) 式中,D为删除率基数,本文取0.01;Ir为删除进化速度,本文取0.01;Fr为删除加速度,其表达式为 (9) 式中,Cr为设置的删除加速点,Cr∈N,且Cr 本文以Ansys为开发环境,编制了单元生死并行的双向渐进结构优化程序.双向迭代优化流程如图2所示. 图2 双向拓扑优化流程图 本文通过一个算例来验证程序的可行性.简支梁跨中受集中力作用.优化目标是寻找结构的最优构形,拓扑优化过程如图3所示.新生单元不断出现在高应力区域,没有空间限制,但这并不意味着单元会持续生长.当单元的增加无法有效降低相邻高应力单元的应力水平时,在下一轮的迭代中这些单元则会被删除.从图3中可以看出,最终拓扑构形中的单元绝大多数为新生单元,超出了原结构的范畴.但是此程序同样适用于有边界限制的结构. 图4为一预应力混凝土简支梁,梁长L=8 m,矩形截面,承受2个集中力荷载F=10 kN.混凝土弹性模量Ec=34.5 GPa,泊松比μc=0.3.采用平面实体单元建模.下面按预应力度λ=0,0<λ<1,λ>1三种情况分别进行讨论.3种预应力度下的结构性能指标曲线如图5所示. 图3 简支梁双向优化过程 图4 预应力混凝土梁示意图(单位:m) 图5 结构进化指标 预应力度λ=0,即普通钢筋混凝土梁.由图5可见,随着优化的进行,性能指标Pin由1.0逐渐增大,在第64次迭代时达到峰值1.37.随后,性能指标Pin急剧下降,说明此时单元删除率远大于单元生长率.过多的单元剔除使得结构产生较大的位移.本文提出的算法为启发式算法,Ra与Rr的选取并无严格的数学证明,无法得到精确解.考虑到优化过程中高应力单元生长与低应力单元删除的平衡,Ra与Rr两者之和应接近于1,并且Rr应远小于1.如果两者比例失衡,将会出现单元只增不减或只减不增,甚至是不增不减的无效拓扑. 普通钢筋混凝土梁的拓扑构形如图6(a)所示.考虑到结构的对称性,取结构的一半.根据拓扑构形构建的拉压杆模型如图6(b)所示,由图可以看出,有的钢筋(拉杆)从底部弯起,用以抵抗剪跨内产生的拉应力.力学模型可采用桁架模型.Schlaich等[1]构建的拉压杆模型如图6(c)所示,考虑到实配箍筋情况,文献[1]在剪跨内采用了竖向拉杆以抵抗拉应力. 图6 钢筋混凝土梁 在混凝土梁的两端施加p=5 kN的等效预应力荷载,结构进化曲线如图5所示.性能指标Pin在第90次迭代时达到最大值1.58,为3条进化曲线峰值中的最大值. 比较图6(a)与图7(a)可发现,预应力的施加明显改变了结构的传力路径.从图7(b)可以看出,相对于钢筋混凝土梁,部分预应力混凝土梁拉压杆模型的底部拉杆长度变短,使得传力路径更加直接.同时,部分预应力混凝土梁拉压杆模型中的压杆增多,并有与最外围的“拱形”压杆汇合的趋势,结构受力逐渐由“梁行为”向“拱行为”过度.力学模型可采用桁架-拱叠合模型.Schlaich等[1]构建的拉压杆模型如图7(c)所示,底部拉杆缩短,并与竖向方向的拉杆(箍筋)连接. 图7 部分预应力混凝土梁(p=5 kN) 为进一步考察预应力度为0<λ<1时不同预应力水平引起的传力路径的变化,分别施加p=16,30 kN的等效预应力进行分析.拓扑优化结果以及拉压杆模型构形如图8所示.比较图7(b)、图8(b)与图8(d)可以看出,随着预应力水平的提高,拉压杆模型中的拉杆数量进一步减少.以集中力作用点为顶点,压杆之间的夹角逐渐减小,呈“归并”趋势.由于拓扑结构中杆件的粗细代表杆件受力的相对大小,比较图7(a)、图8(a)与图8(c)可知,随着预应力水平的进一步提高,“拱形”压杆逐渐“变粗”,结构受力的“拱行为”增强;处于拱形压杆下方的其他拉、压杆逐渐变细,结构受力的“梁行为”削弱.当λ>1时,结构呈现为“拱形构形”(见图9(a)). 图8 部分预应力混凝土(p=16,30 kN) 在混凝土梁两端施加p=60 kN的等效预应力,此时控制截面受拉区边缘不出现拉应力.其性能指标曲线如图5所示,在第74次迭代时,性能指标Pin达到最大值1.42,略高于无预应力混凝土.在进化过程中,虽然结构体积整体呈下降趋势,但过大的预应力使得结构应变能减小缓慢,因此进化曲线相对平缓.由图9(b)可以看出,拉压杆模型仅包含压杆,结构受力由“梁行为”转换为“拱行为”.力学模型可采用拱模型.图9(c)为Schlaich等[1]提出的全预应力混凝土梁的拉压杆模型.其力学模型为拱-桁叠合模型. 图9 全预应力混凝土(p=60 kN) 1) 渐进结构拓扑优化是寻找混凝土结构传力路径的一种有效方法.本文在双向渐进拓扑优化算法中,以体积应变能为效率指针,通过引入单元生长与删除加速度因子,消除了无效拓扑的发生,有效增强了双向渐进优化过程的稳定性. 2) 利用自行编制的双向拓扑优化程序,针对2个集中力作用工况,得到了不同预应力度下梁的拓扑构形,揭示了钢筋混凝土、部分预应力混凝土及全预应力混凝土梁的传力路径和合理力学模型:钢筋混凝土梁可采用桁架模型,部分预应力梁可采用桁架-拱叠合模型,全预应力梁可采用拱模型或拱-桁叠合模型.运用本文算法及程序,同样可以得到其他受力工况下的最优拓扑构形. ) [1] Schlaich J, Schafer K, Jennewein M. Toward a consistent design of structural concrete [J].JournalofthePrestressedConcreteInstitute, 1987,32(3): 74-150. [2] Collins M P, Mitchell D. A rational approach for shear design [J].ACIStructuralJournal, 1986,83(6): 925-933. [3] Collins M P, Mitchell D. Shear and torsion design of prestressed and nonprestressed concrete beams [J].PCIJournal, 1980,25(2): 32-100. [4] American Association of State Highway and Transportation Officials. AASHTO LRFD bridge specifications [S]. Washington: John Wiley & Sons, 2007. [5] ACI Committee 318. ACI 318M—08 Building code requirements for structural concrete and commentary [S]. Michigan, USA: American Concrete Institute, 2008. [6] Kumar P. Optimal force transmission in reinforced concrete deep beams [J].Computers&Structures, 1978,8(2): 223-229. [7] Ali M A, White R N. Automatic generation of truss model for optimal design of reinforced concrete structures [J].ACIStructuralJournal, 2001,98(4): 431-442. [8] Liang Q Q. Topology optimization of strut-and-tie models in reinforced concrete structures using an evolutionary procedure [J].ACIStructuralJournal, 2000,97(2): 322-332. [9] Bruggi M. Generating strut-and-tie patterns for reinforced concrete structures using topology optimization [J].Computers&Structures, 2009,87(23/24): 1483-1495. [10] Liang Q Q. Generating optimal strut-and-tie models in prestressed concrete beams by performance-based optimization [J].ACIStructuralJournal, 2001,98(2): 226-232. [11] Bruggi M. On the automatic generation of strut and tie patterns under multiple load cases with application to the aseismic design of concrete structures [J].AdvancesinStructuralEngineering, 2010,13(6): 1167-1181. [12] Biondini F, Bontempi F. Optimal strut-and-tie models in reinforced concrete structures [J].ComputerAssistedMechanicsandEngineeringSciences, 1999,6(3): 279-293. [13] Biondini F, Bontempi F. Stress path adapting strut-and-tie models in cracked and uncracked R.C. elements [J].StructuralEngineeringandMechanics, 2001,12(6): 685-698. [14] Kwak H G, Noh S H. Determination of strut-and-tie models using evolutionary structural optimization [J].EngineeringStructures, 2006,28(10): 1440-1449. [15] He Z Q, Liu Z. Optimal three-dimensional strut-and-tie models for anchorage diaphragms in externally prestressed bridges [J].EngineeringStructures, 2010,32(8): 2057-2064. [16] Tanskanen P. The evolutionary structural optimization method theoretical aspects [J].ComputerMethodsinAppliedMechanicsandEngineering, 2002,191(47/48): 5485-5498.
1.3 双向优化过程
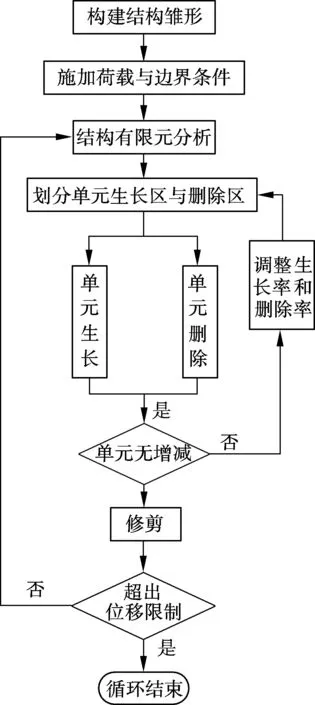
1.4 算例
2 预应力简支梁拉压杆模型

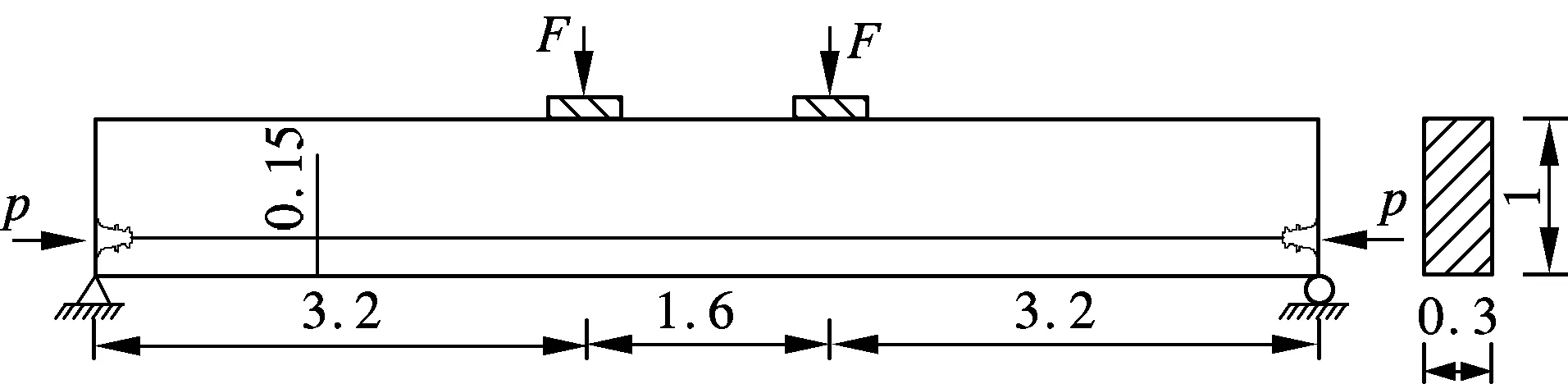

2.1 钢筋混凝土梁(λ=0)
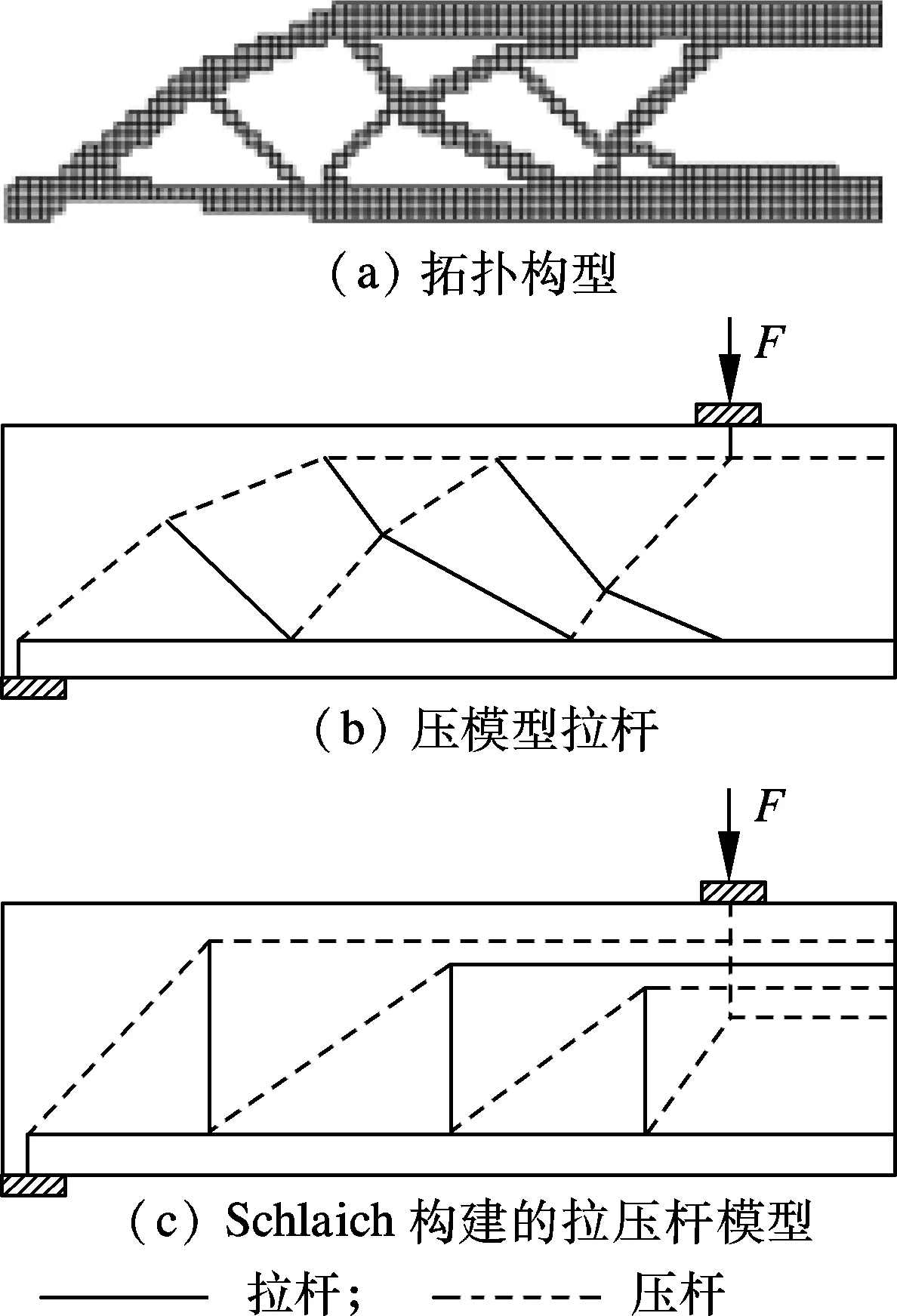
2.2 部分预应力混凝土梁(0<λ<1)

2.3 全预应力混凝土梁(λ>1)

3 结论
