基于ARCH 族模型的超灵便型船运价指数研究

王 铖，林国龙，丁 一

(上海海事大学 物流研究中心，上海201306)

波罗的海干散货运价指数(BDI)是反映世界经济走势的晴雨表，而超灵便型船运价指数(BSI)是BDI 的重要组成部分。超灵便型船既能适应船舶大型化的趋势又有自身的灵便性，可根据航运市场走势调节货源，既可以运输巴拿马型船的煤炭谷物等大宗散货，又可以运输小灵便型船的化肥、水泥等小宗散货。BSI 指数自2005 年7 月正式发布至今，人们对其研究很少，笔者运用ARCH 族模型分析BSI 日收益率序列的条件异方差性和非对称性，并结合实际分析了特殊时期的波动特性，对把握超灵便型船运市场的动态有重要意义。

不少学者对波罗的海干散货运价指数进行了研究，JANE 等［1］通过建立AR－GARCH 模型和GMM 回归分析得出了船队规模增长与干散货市场上运价波动的关系。OKAN［2］运用多变量模糊逻辑预测模型(M－FILF)和模糊时间序列相关理论对干散货市场的波动性进行研究并做出短期预测。陆从克等［3］使用GARCH 模型分析了BDI 收益率序列的波动集聚效应并结合实际分析了特别波动的原因。杨华龙等［4］对4 种船型建立GARCH 模型并通过实例验证了波罗的海干散货运价指数波动的敏感性和持续性规律。施文明等［5］对波罗的海干散货运价指数收益率序列分区间建立EGARCH 模型来考察“好消息”和“坏消息”对收益率的非对称性影响。翟海杰等［6］通过对BDI 指数的收益率序列建模，比较不同分布情况下GARCH 模型的优劣。

1 数据选取与预分析

笔者选取2005 年7 月至2012 年5 月波罗的海交易所发布的超灵便型船运价指数，共有1 732个观测数据，BSI 序列如图1 所示。

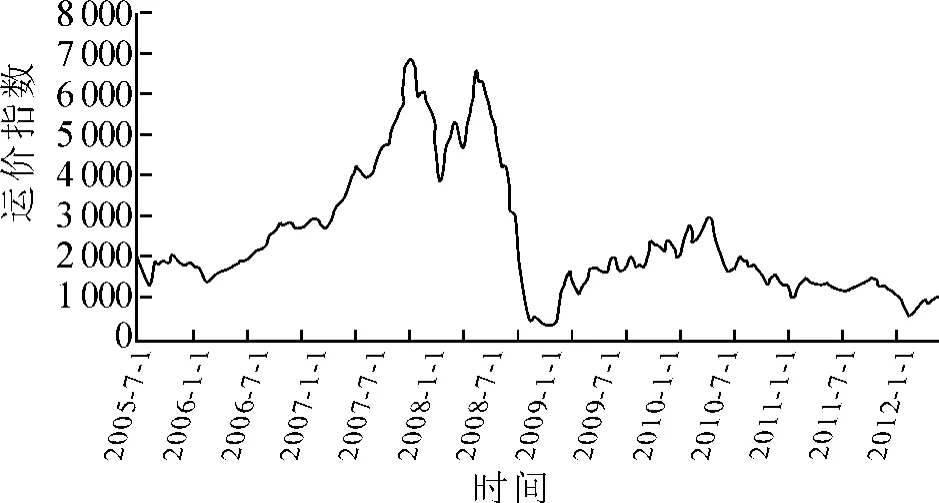
图1 BSI 序列图

由BSI 序列图发现BSI 序列波动性较大，存在长期趋势和季节趋势。对BSI 序列取自然对数，然后进行一阶差分得到BSI 日收益率序列Rt，日收益率序列基本统计特征如图2 所示。Rt的具体形式如式(1)所示。

式 中:Rt为BSI 的 日 收 益 率;Yt为BSI 的 日运价指数。

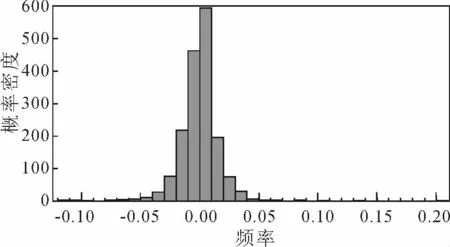
图2 BSI 日收益率序列基本统计特征

由图2 计算可得，BSI 日收益率序列的偏度为0.51，峰度为21.09，BSI 日收益率序列具有尖峰厚尾的特征，JB 检验的相伴概率为0.000 0，不能认为日收益率序列服从正态分布。

由BSI 日收益率序列图(图3)可以看出，日收益率序列围绕0 上下波动，没有明显的上升或下降趋势，初步判断日收益率序列趋于平稳，利用ADF 检验日收益率序列的平稳性，由ADF 检验可知t 值远远小于相关水平下的概率值，BSI 日收益率序列为平稳序列。

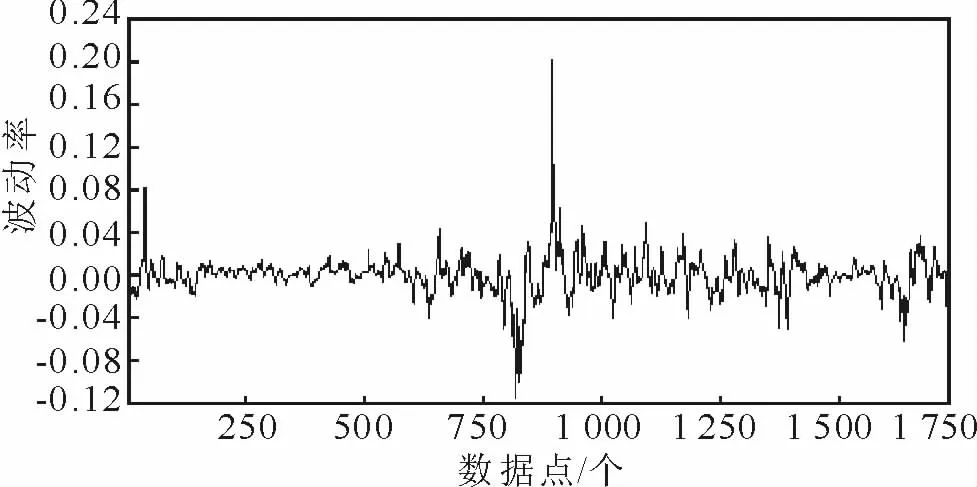
图3 BSI 日收益率序列图

2 BSI 日收益率序列的波动性分析

2.1 BSI 日收益率序列的异方差性分析

自回归条件异方差(ARCH)模型［7］被广泛应用于金融时间序列分析，ARCH 模型由均值方程和方差方程组成。均值方程通过ARMA 模型确定，即由自相关函数(ACF)和偏自相关函数(PACF)确定BSI 日收益率序列的模型拟合的基本形式，由ACF 图和PACF 图(图4)可以看出BSI 日收益率序列的自相关函数呈拖尾，偏自相关函数呈2 阶截尾，通过相关分析得出以AR(2)模型拟合BSI 日收益率序列，AR(2)拟合模型如式(2)所示:

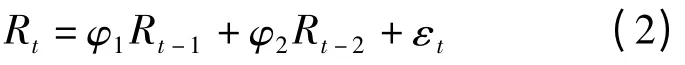
由Eviews 可得出AR(2)模型的各参数，BSI收益率序列的拟合方程如式(3)所示:

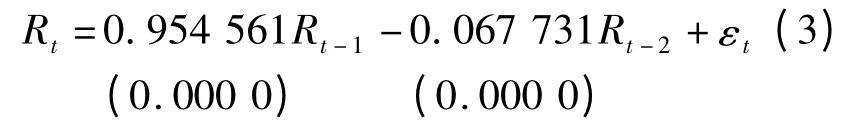
(括号内数字为估计参数对应的p 值，下同)

R2=0. 8，对数似然值为5 919. 069，AIC =－6.844，SC=－6.838。

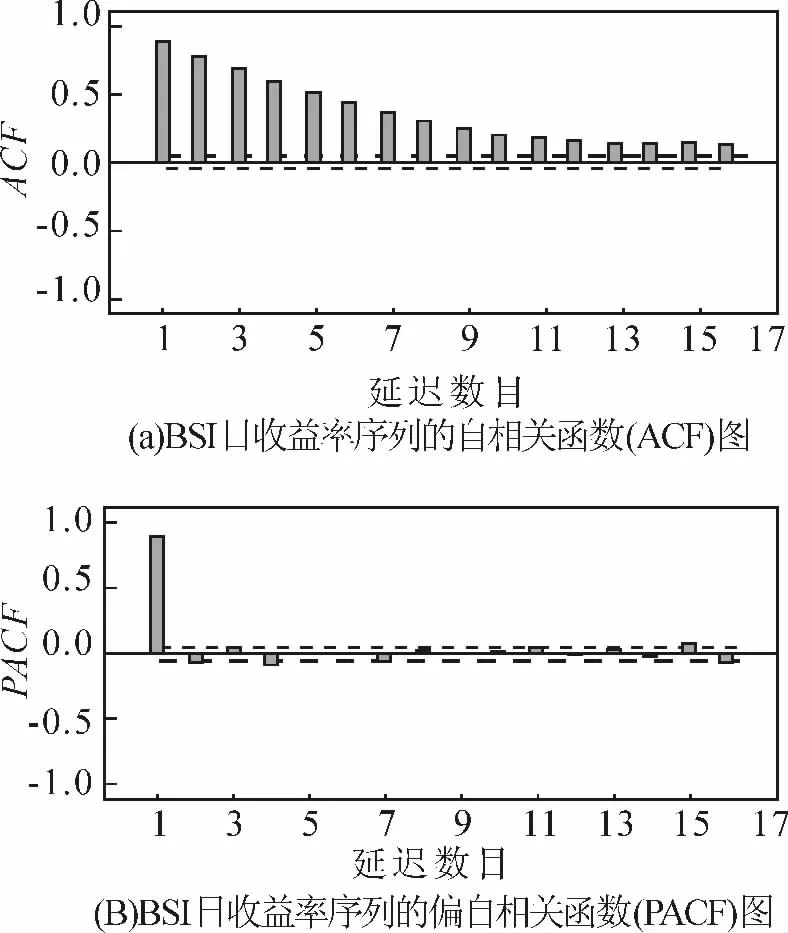
图4 BSI 日收益率序列自相关函数(ACF)和偏自相关函数(PACF)图

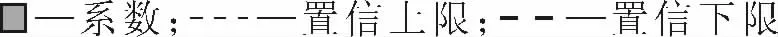
观察拟合方程式(3)的残差序列，可得出拟合方程的残差序列图(图5)，由图5 可以看出BSI日收益率序列存在波动成群的现象，较小的波动伴随着较小的波动，较大的波动伴随着较大的波动，BSI 日收益率序列可能存在条件异方差性。

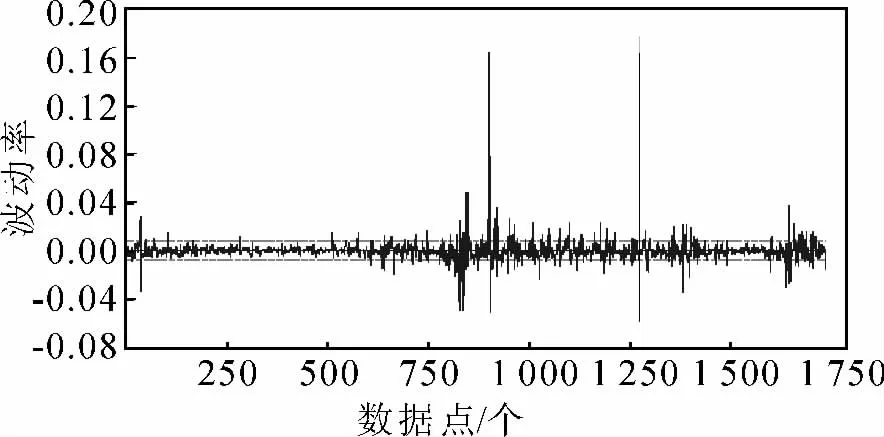
图5 BSI 日收益率序列回归方程残差图

利用ARCH LM 检验收益率序列是否存在ARCH 效应，Eviews［8］检验结果显示ARCH(1)的x2检验的相伴概率p 值为0.000 6，小于显著性水平0.05，说明模型中的随机误差项存在ARCH 效应，增加阶数继续检验随机误差项，经过ARCH LM 检验得到滞后阶数为10 时仍存在ARCH 效应，说明BSI 收益率序列存在高阶异方差性，即需运用广义自回归条件异方差模型(GARCH)［9］对其进行分析。GARCH 模型用一个或者两个滞后值代替许多μt2的滞后值。GARCH(p，q)模型一般形式如式(4)所示:

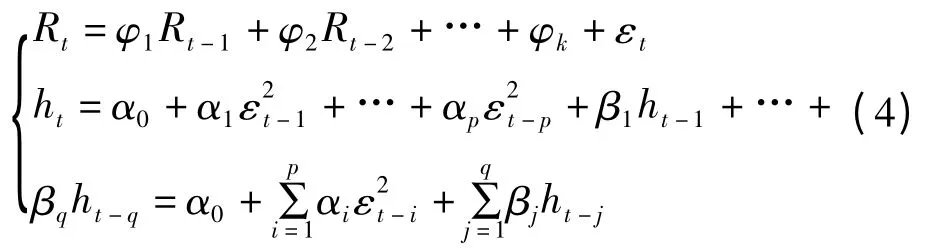
其中:Rt为t 时刻的收益率;εt为均值方程的干扰项;ht为εt在t 时刻的条件方差;ε2t－p 为ARCH(p)项;ht－q为GARCH 项;p 和q 分别为滞后的阶数;αp，βq，φk为对应的参数。

一般情况下GARCH(1，1)模型能够描述大部分的金融时间序列，因此，以GARCH(1，1)模型为基础，采用Eviews 默认的正态分布假设建模，根据AIC 和SC 准则进行模型定阶，结果如表1 所示。

表1 GARCH(p，q)模型估计结果

经过综合考虑，BSI 收益率序列选取GARCH(2，1)模型。由于BSI 日收益率序列存在尖峰厚尾性，不是正态分布，因此考虑分别使用正态分布、t 分布、GED 分布来进行GARCH(2，1)模型建模，最后比较确定模型的各参数，基于不同分布的GARCH(2，1)模型的估计结果如表2 所示。

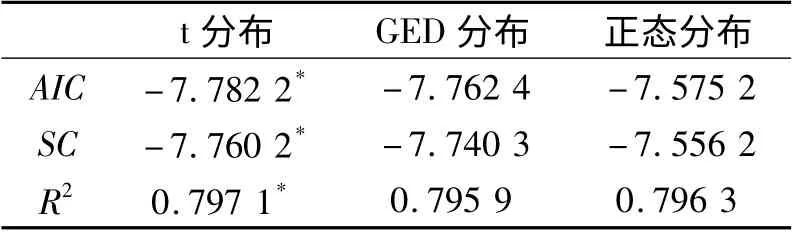
表2 不同分布的GARCH(2，1)模型估计结果

由表2 可知，基于t 分布的GARCH(2，1)模型的各项指标明显优于GED 分布和正态分布，最终采用基于t 分布的GARCH(2，1)模型来描述BSI 日收益率序列。由Eviews 得出该模型的各参数的极大似然估计结果，模型如式(5)所示:

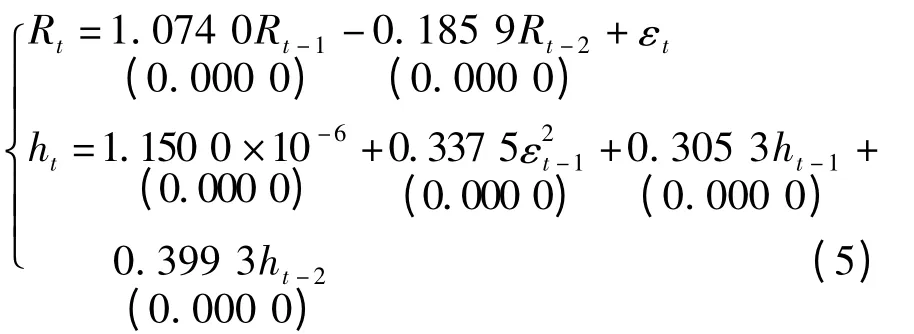
对GARCH(2，1)模型均值方程的残差再进行ARCH LM 检验，可得出滞后1 阶的相伴概率为0.747 8，认为残差序列不存在ARCH 效应，GARCH(2，1)模型消除了残差序列的条件异方差性。

对GARCH(2，1)模型结果进行分析，系数项之和(α+β)为1.11 ＞1，表明2005 年至2012 年超灵便型船运市场遭受各类外部冲击的持续性较大，冲击影响会扩散，波动持续时间会较长，这也反映了2007 年以来BSI 指数波动加剧的现象。

为了更好地描绘2005 年至2012 年BSI 指数波动的特征，建立BSI 日收益率序列的条件方差序列图，如图6 所示。

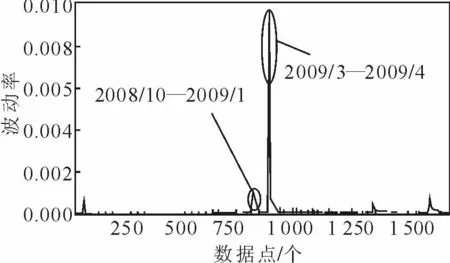
图6 BSI 日收益率序列条件方差图

由图6 可以看出，BSI 日收益率序列出现过2次大的波动，第一次大的波动出现在2008 年10月至2009 年1 月期间，BSI 指数由259 9 点迅速下跌至历史最低点389 点，跌幅达到85%。BSI指数的下跌主要受美国经济危机引发全球经济增长放缓的影响，进而影响到国际煤炭贸易与粮食贸易的海运量，致使超灵便型船的5 条航次期租航线日租金水平持续下跌。第二次较大的波动出现在2009 年3 月至2009 年4 月期间，BSI 指数震荡回升，主要是受粮运旺季的影响，美湾和南美出口的谷物货盘增加催生了超灵便型船5 条航次期租航线日租金水平的回升。

2.2 BSI 日收益率序列的非对称性分析

金融时间序列往往存在杠杆效应，等量利好消息与等量利空消息对市场的冲击是不同的，允许波动率对市场下跌的反应比对市场上升的反应更加迅速［10］。笔者分别采用TARCH 模型和EGARCH模型来研究BSI 日收益率序列的非对称性。

2.2.1 TARCH 模型分析

门限ARCH 模型(TARCH)的条件方差表达式如式(6)所示:

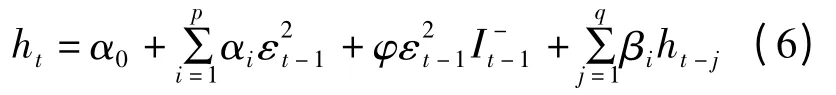
利用Eviews 软件分析BSI 日收益率序列可以得出TARCH 模型的各参数，BSI 日收益率的TARCH 模型如式(7)所示:

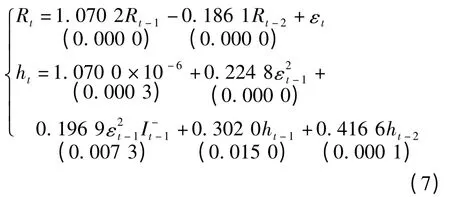
R2=0.797 2，对数似然值为6 739.65，AIC =－6.786 8，SC=－7.761 5。

对TARCH 模型结果进行分析，杠杆效应项系数φ=0.196 9，说明BSI 日收益率具有杠杆效应，主要效果是使波动加大，出现利好消息时会对BSI 日收益率带来0.224 8 倍的冲击，出现利空消息时会对BSI 日收益率序列带来0.421 7 倍的冲击，利空消息比等量的利好消息产生更大的波动，这一结果将在EGARCH 模型中得到验证。

2.2.2 EGARCH 模型分析

指数GARCH 模型(EGARCH)的条件方差表达式如式(8)所示:

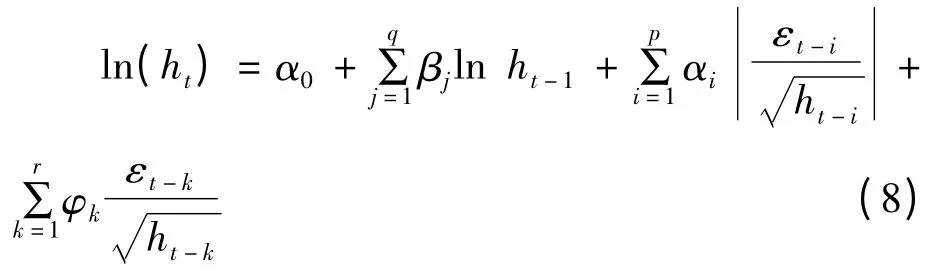
其中:φk体现信息的非对称性，φk＞0 表示上涨信息引发的波动比下跌信息引发的波动大，φk＜0表示下跌信息引发的波动比上涨信息引发的波动大。

利用Eviews 软件分析BSI 日收益率序列可以得出EGARCH 模型的各参数，BSI 日收益率的EGARCH 模型如式(9)所示:

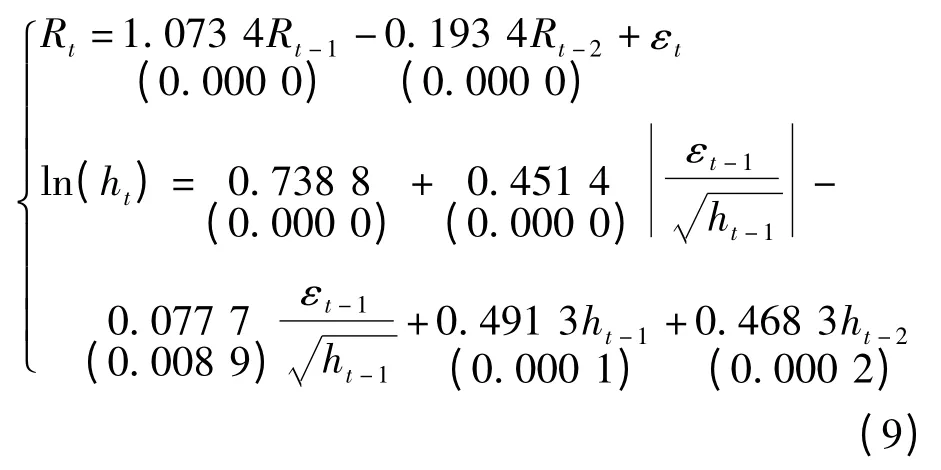
R2=0.796 9，对数似然值为6 746.25，AIC =－7.794 4，SC=－7.769 1。

对EGARCH 模型结果进行分析，当出现“利好消息”即εt－1＞0 时，该信息会对BSI 日收益率带来0.373 7 倍的冲击，当出现“利空消息”即εt－1＜0时，该信息会对BSI 日收益率带来0.529 1倍的冲击，利空消息比利好消息对BSI 日收益能产生更大的影响，这一点也与TARCH 模型的结果相吻合。

3 结论

(1)BSI 日收益率序列为平稳序列，具有尖峰厚尾性，通过ARCH LM 检验得出收益率序列存在高阶ARCH 效应，GARCH(2，1)模型能够较好地消除该异方差性。

(2)BSI 日收益率序列存在族聚现象，较小的波动伴随着较小的波动，较大的波动伴随着较大的波动。

(3)基于t 分布的GARCH 模型要优于正态分布和GED 分布的模型，更能够准确反映BSI 日收益率序列的波动特征。

(4)美国金融危机影响全球散货贸易量和超灵便型船运市场，BSI 指数序列在2008 年至2009年间存在较大的波动。

(5)BSI 日收益率序列为非对称序列，存在杠杆效应，等量的利空消息比利好消息对日收益率序列产生更大波动。

［1］ JANE J X，TSZ L Y，PETER B M. The dynamics between freight volatility and fleet size growth in dry bulk shipping markets［J］.Transportation Research Part E ，2011，47(6):983－991.

［2］ OKAN D. A multivariate model of fuzzy integrated logical forecasting method (M－FILF)and multiplicative time series clustering:a model of time－varying volatility for dry cargo freight market［J］. Expert Systems with Applications，2012(12):4135－4142.

［3］ 陆从克，赵刚. ARCH 族模型在干散货运价指数分析中的应用［J］.系统工程，2008(9):50－56.

［4］ 杨华龙，刘金霞. 波罗的海干散货运价指数波动性研究［J］.中国航海，2011(9):84－88.

［5］ 施文明，杨忠直.基于EGARCH 的运费收益率波动风险［J］.大连海事大学学报，2011(8):55－57.

［6］ 翟海杰，李序颖. 基于不同分布的GARCH 族模型的波罗的海干散货运价指数波动率研究［J］. 上海海事大学学报，2009(9):59－64.

［7］ ENGLE R F. Autoregressive conditional heteroskedasticity with estimates of the variance of U. K inflation［J］.Econometrica，1982(50):987－1008.

［8］ 易丹辉.数据分析与Eviews 应用［M］.北京:中国人民大学出版社，2008:245－269.

［9］ BOLLERSLEV T. Generalized autoregressive conditional heteroscedasticity［J］.Journal of Econometrics，1986(31):307－327.

［10］高铁梅.计量经济分析方法与建模［M］.北京:清华大学出版社，2006:171－199.