求解TSP 问题的改进蚁群算法

王 胜，谭家政，刘 勇，邱芹军

(三峡大学 智能视觉与图像信息研究所，湖北宜昌443002)

TSP 问题是一个经典的NP 难问题，经常被作为测试解决NP 难问题的各种启发式算法的案例。它对于科学和工程技术领域中的大量组合优化问题，尤其是NP 完全问题的求解有着极为重要的价值［1］。目前，求解TSP 问题的比较好的启发式算法主要有粒子群算法［2］、遗传算法、模拟退火算法、人工免疫算法和蚁群算法。在通常情况下，蚁群算法得到的最短路径要好于其他的启发式算法。

蚁群算法以先验信息和信息素的正反馈作用来引导每只蚂蚁的行为，使得蚁群整体上逐渐向全局最短路径靠拢。但是基本蚁群算法对信息素的处理过于粗糙，对已经寻找到的最短路径缺乏较强的敏感性，使得算法的收敛速度太慢。为了加快蚁群算法的收敛速度，有学者提出了带精英策略的蚁群算法［3］。该算法在已经找到的最短路径和基本蚁群算法的基础上，额外加了一些信息素，虽然能使每只蚂蚁向已经找到的最短路径进一步靠拢，但是相对于那些在每次迭代中蚂蚁走过的非最短路径，这种靠拢趋势并不明显。且一旦陷入了局部最优，就很难跳出来，从而使得到全局最短路径的概率比较低。针对这个问题，又有学者提出了最大最小蚁群算法［4－6］。它能使每只蚂蚁以较大的概率访问每条可能是全局最短路径一部分的路径，从而避免了陷入局部最优。但是，它有一个较为明显的缺点，就是降低了蚂蚁在已经得到的全局最短路径附近较小范围内探索的能力，从而很大程度上降低了最大最小蚁群算法得到全局最优解的概率。

为了加快蚁群算法的收敛速度，且使蚁群算法能以较大的概率找到问题的全局最短路径，近些年来，不断有学者提出各种各样的对蚁群算法的改进策略。如顾军华等提出了一种改进的用于求解TSP 问题的蚁群优化算法［7－8］;李将军等提出了采用动态的先验信息权值和信息素权值的自适应调整策略，提高了蚁群算法的求解性能［9］。

但是以上改进算法都只是在基本蚁群算法的基础上作了较小的改动，很难从根本上解决基本蚁群算法收敛速度较慢，容易陷入局部最优的问题。因此笔者对蚁群算法做了一些适当的改进。

1 求解TSP 问题的改进蚁群算法的思路

1.1 利用节约算法求初始最短路径

改进算法先用节约算法得到的路径将蚁群定位在一个离全局最短路径较近的区域，再使蚁群以较小的迭代为代价找到一个局部最短路径，若经过多次迭代后，蚁群没有在该局部最短路径附近找到一个更优的路径，则对次局部最短路径及附近区域施行禁忌策略，使蚁群跳到下一个可能存在最短路径的区域进行搜索，快速找到下一个局部最短路径，如此下去直到找到全局最短路径为止。

蚁群算法很难最终收敛到全局最短路径，其中一个很重要的原因是，它选择的初始路径离全局最短路径较远，为了向全局最短路径逐步靠拢，所要越过的局部最短路径较多。为了弥补蚁群算法的不足，使蚁群算法能以更大的概率选择全局最短路径，就必须为蚁群算法设置一个离全局最短路径较近的初始路径。节约算法是一种高效的精确启发式算法，它得到的解一般要好于其他精确启发式算法，有较好的交叉性能，同时为了提高算法的效率，应把节约算法找到的路径作为蚁群算法的初始最短路径，对信息素进行更新。

1.2 概率选择公式的改进

在传统蚁群算法中，蚂蚁把将要选择路径的长短作为唯一的先验知识，优先选择较短的路径。但是，传统的蚁群算法中蚂蚁在选择路径时是通过对路径进行单向的评价，这在很大程度上降低了先验信息的准确性。因此，可以考虑将路径的长度在所有与其直接相连的路径中的排名作为除了路径的长短之外的另一部分先验知识，使蚂蚁在选择路径时有更充分的先验知识可以运用，选择的路径更优，这有利于提高算法的寻优能力。故将蚂蚁的概率选择公式改成:

式中:allowedk为第t 次迭代中第k 只蚂蚁还未访问的城市序号组成的集合;η′ij为路径(i，j)在所有与i 相连的路径中的排名的倒数;γ 为其重要程度。

1.3 蚂蚁的状态转移规则改进

有时某一个城市到另外两个或多个城市的距离与路径上的信息素的量相差无几，让蚂蚁根据概率公式直接选择较优的城市会比较困难。在这种情况下，为了能使蚂蚁选择到最优的路径，需要对蚁群算法的概率公式作一些调整。

在蚂蚁选择下一个将要访问的城市时，产生一个0 ～1 之间的随机数rand。如果

R0为事先给定的0 ～1 之间的参数，则在第t次迭代中，位于城市i 的蚂蚁下一个要访问的城市为:

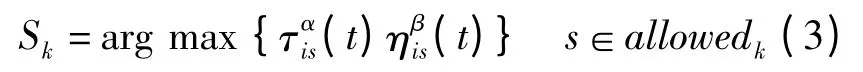
否则，该蚂蚁按照式(1)选择下一个将要访问的城市。

1.4 信息素更新策略改进

带精英策略的蚁群算法的信息素更新策略为:

式中:Δτ*为精英蚂蚁引起的路径(i，j)上的信息素的增加量;σ 为精英蚂蚁的个数;L*为找出的最优解的长度。

从该信息素更新策略中可以看出，当有一只或少数几只蚂蚁找到新的最短路径时，最短路径上的信息素相对于在本次迭代中蚂蚁经过的路径增加得并不明显。因此将导致蚁群整体上很难对找到的最短路径做出快速而有效的反应，从而有可能使该最短路径在探索中被湮没掉，导致蚁群对新发现的最短路径不敏感，并降低了解的收敛速度。当经过多次迭代后，大部分蚂蚁逐渐向该最优路径逼近时，经过该最短路径的蚂蚁会很多，σ 值会变得很大，使得最短路径上的信息素也会变得很大，由于蚁群对新发现的最短路径解不敏感，使得蚁群在该最优解的位置停滞不前。

为了使蚁群对已找到的最短路径有较稳定的敏感度，将式(1)修改为:

式中:V 为1 到蚂蚁个数之间的一个参数，取一个较大值。这样相对于蚂蚁在本次迭代中经过的路径，新的最短路径的影响会更明显，就会使蚁群能快速地在新的最短路径附近有效地探索，从而加快蚁群的收敛速度。当蚁群在逐渐向已找到的全局最短路径靠拢时，全局最短路径上的信息素已经足够多，收敛速度已经足够快，没有必要进一步增加最短路径上的信息素的量。而且收敛速度过快，会使蚁群丧失在已找到的最优路径周围发现新的最优路径的能力，因此将式(4)改为:

1.5 信息素最大最小限制

由于该算法在理论上已经具备跳出局部最优解的能力，因此利用最大最小蚁群算法中的策略，对信息素作最大最小限制的主要目的不是为了避免蚁群算法出现停滞状态，而是为了能使蚁群跳出局部最优的速度更快。为了使蚂蚁能在找到的最短路径附近较小的范围进行探索，可适当放宽对信息素的最大限制。

经过t 次迭代，信息素经过式(5)更新后，有:

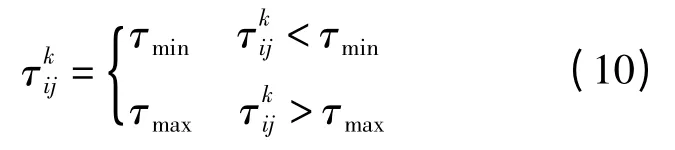
为了使τmax能在信息素更新的过程中被达到，令Q ＞(1－ρ)τmaxL*。

1.6 利用禁忌策略避免蚁群停滞于局部最短路径

大多数基本蚁群算法及其改进算法的缺点是，即使在已经找到的最优路径附近找了很多次，仍然没有找到更好的解，在基本可以断定该问题的全局最优解不在其附近的情况下，蚁群仍不能在适当的时候跳出该区域。

为了处理这种情况，首先禁忌掉该最短路径及其附近的路径，然后寻找一个新的可能出现全局最优解的区域。为了充分利用经验信息，把没有被禁忌掉的路径中的最短路径作为新的全局最短路径来对信息素进行更新。

(1)建立禁忌表forb［n，m］，禁忌掉经过较多次迭代没更新的局部最短路径及其附近的路径。令forb［i，j］=0，i=0，1，2，…，n;j =1，2，…，m;其中，n 为迭代次数;m 为蚂蚁的个数。

(2)如果经过连续l 次迭代，已找到的最短路径都没有更新，则在所有已找到的路径中禁忌掉该最短路径及其附近路径，令forb［besti，bestj］=1，(besti，bestj)∈G。其中，G 为已经找到的所有路径中，长度大于或等于上次被禁忌掉的最短路径，且排名在前T 名以内的路径上经过的蚂蚁的序号及该路径所在迭代的序号对构成的集合。

(3)在没有被列入禁忌表的所有蚂蚁经过的路径长度比刚被禁忌掉最短路径长Δd 的路径中，寻找最短路径作为新的全局最短路径，利用式(8)对信息素进行更新。

(4)每一次迭代后，在所有蚁群找到的路径中，禁忌掉路径长度与禁忌表中的某条路径的长度相等的路径，再在此次迭代中没有被禁忌掉的路径中寻找最短路径，如果该最短路径要优于在此次迭代之前没有被列入禁忌表中的路径中的最短路径，则将该最短路径作为新的已经找到的全局最短路径。否则，不对全局最短路径进行更新。

2 求解TSP 问题的改进蚁群算法步骤

求解TSP 问题的改进蚁群算法步骤如下:

(1)初始化参数，令n=1;

(2)利用节约算法得到初始最短路径;

(3)将蚂蚁放在起始城市上;

(4)产生随机数rand，如果rand ＜R0，蚂蚁按照式(3)选择下一个城市，否则，按照式(1)选择下一个城市;

(5)如果蚂蚁访问完所有城市，让蚂蚁回到起始城市上，否则跳到步骤(4);

(6)如果所有蚂蚁都已回到起始城市，进行下一步，否则跳到步骤(3);

(7)从所有已访问的没有被禁忌掉的路径中选出最短路径，作为已找到的最短路径，结合该次迭代中所有蚂蚁的访问路径，按照式(8)对这些路径上的信息素进行更新，并利用式(10)对信息素进行修正;

(8)如果连续迭代l 次，最短路径都没有更新，将该最短路径及其附近路径放入禁忌表中;

(9)如果迭代次数等于预先设定的最大迭代次数，则算法结束;否则，令迭代次数n =n +1，跳到步骤(3)。

3 仿真实验

采用TSPLIB 中eil51 问题，分别对带精英策略的最大最小蚁群算法和笔者改进的蚁群算法进行测试，并与文献［9］中的改进文化蚁群算法进行比较。参数设置为:n=100，m =50，α =4.5，带精英策略的最大最小蚁群算法中β =4，改进的蚁群算法中β =0，γ =3，ρ =0.75，Q =800，V =50，l=20，T =1，Δd =0，R0=0.3，τmin=1.00，τmax=7.00，表1 为经过20 次独立实验后的结果比较，表明笔者改进后的算法比其他算法能得到更短的最短路径，而且更稳定。

图1 展示了求解eil51 问题过程中，随着迭代次数的增加，带精英策略的最大最小蚁群算法和笔者改进的蚁群算法找到的最短路径朝全局最短路径收敛的性能，从图1 中可以看出，带精英策略的最大最小蚁群算法虽然能不断收敛，但是最后收敛到的解并不十分优良，与改进的蚁群算法比它的最优解要大得多。因此，与带精英策略的最大最小蚁群算法相比，笔者改进的蚁群算法具有更好的寻优能力。

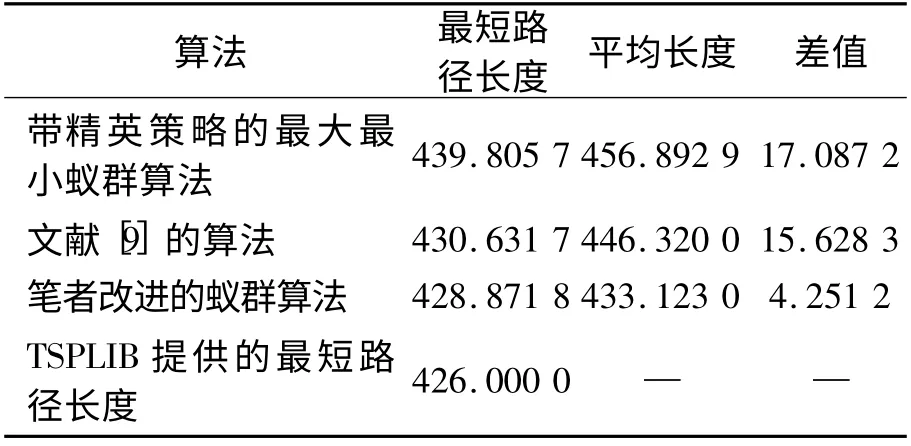
表1 eil51 问题3 种算法结果比较 km

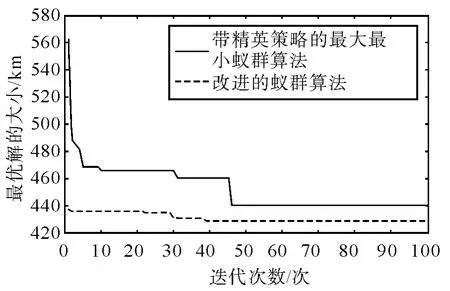
图1 带精英策略的最大最小蚁群算法与笔者改进的蚁群算法的收敛性比较

采用TSPLIB 中eil101 问题，分别对带精英策略的最大最小蚁群算法与笔者改进的蚁群算法进行测试。参数设置为:n =100，m =50，α =4.5，β=4，γ=2.0，ρ=0.75，η′0=0.000 01，Q=200 0，V=101，l=10，T=1，Δd=0，R0=0.3，τmin=1.00，τmax=16.00，表2 为经过20 次独立实验后的结果比较，表明笔者改进后的算法在较大规模TSP 问题上能比带精英策略的最大最小蚁群算法更稳定地得到更短的路径。

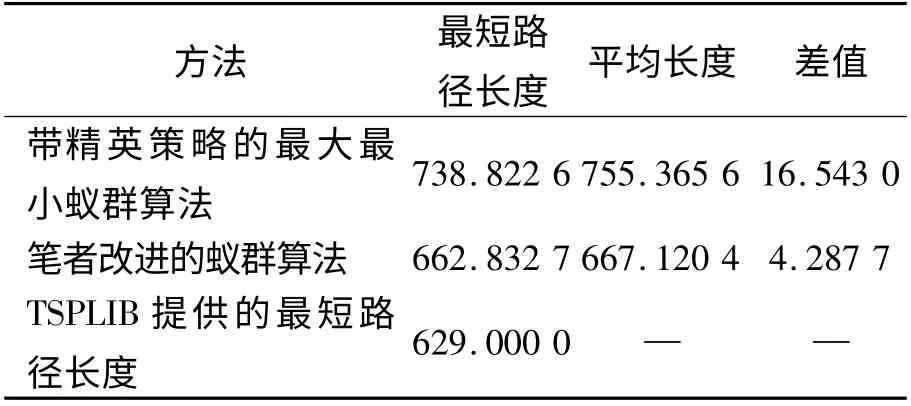
表2 eil101 问题带精英策略的最大最小蚁群算法与笔者改进的蚁群算法结果比较 km

图2 展示了在eil101 问题上带精英策略的最大最小蚁群算法在前10 次迭代就已陷入局部最短路径，而笔者改进的蚁群算法在迭代完30 次后，还能进一步跳出局部最优，最终收敛于一个比带精英策略的最大最小蚁群算法找到的最短路径好得多的最短路径，表明笔者改进的蚁群算法在较大规模的TSP 问题上，收敛性也明显优于带精英策略的最大最小蚁群算法。

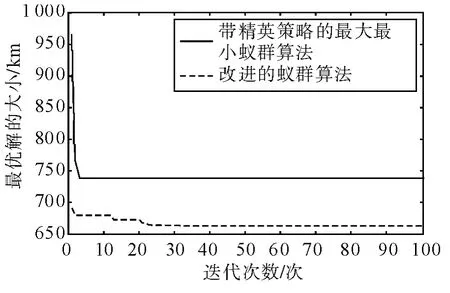
图2 带精英策略的最大最小蚁群算法与笔者改进的蚁群算法的收敛性比较

从表1 和表2 对照中可以看出，不论对于小规模还是较大规模的TSP 问题，每次实验中，笔者改进的蚁群算法找到的最短路径的长度都极为稳定，且稳定性强于带精英策略的最大最小蚁群算法。从图1 和图2 可以看出，随着TSP 问题规模的增大，笔者改进的蚁群算法找到的最短路径的质量和带精英策略的最大最小蚁群算法找到的最短路径的质量的差距也在进一步扩大。

4 结论

笔者对带精英策略的最大最小蚁群算法的关键策略作了进一步改进，通过大量实验表明，笔者提出的改进蚁群算法要明显优于带精英策略的最大最小蚁群算法。但笔者提出的改进蚁群算法缺乏对参数的自适应调整策略，采用何种参数才能进一步提高算法的综合性能，以及如何进一步提高算法对大规模TSP 问题的寻优能力，还值得进一步研究。

［1］ 申红莲，张国立，李振涛.一种求解TSP 问题的新算法［J］.计算机工程与应用，2008，44(6):65－67.

［2］ 梁晓磊，李文锋，张煜，等.具有动态拓扑结构的聚类粒子群算法研究［J］.武汉理工大学学报:信息与管理工程版，2011，33(1):22－26.

［3］ BULLNHEIMER B，HARTL R F，STRAUSS C.A new rank based version of the ant system:a computational study［R］.Vienna:University of Vienna，1997.

［4］ STUTZLE T，HOOS H. Improvements on the ant system:introducing max－min ant system［C］//Proceedings of the International Conference on Artificial Neural Networks and Genetic Algorithms.Wien:Springer Verlag，1997:245－249.

［5］ 熊德国，李颖. 蚁群算法在最小极大流问题中的应用［J］. 武汉理工大学学报:信息与管理工程版，2010，32(6):882－885.

［6］ 王越超，李毅. 基于蚁群算法的产品销售渠道优选策略［J］.武汉理工大学学报:信息与管理工程版，2011，33(6):1011－1014.

［7］ 顾军华，范培培，宋庆增，等. 改进的求解TSP 问题文化蚁群优化方法［J］. 计算机工程与应用，2010，46(26):49－52.

［8］ 赵吉东，胡小兵，刘好斌. 改进的蚁群算法及其在TSP 中的应用［J］. 计算机工程与应用，2010，46(24):51－52.

［9］ 李将军，叶仲泉，宫子风.改进蚁群算法及其仿真研究［J］.计算机应用，2008，28(12):94－96.