航空货运动态定价鲁棒优化模型

刘 沁，彭 怡

(南京航空航天大学 民航学院，江苏 南京211100)

动态定价是收益优化的重要手段之一，最初应用在民航客运业的收益管理。用定价进行收益优化的核心是以需求为导向，在一系列约束条件下，找到实现总期望利润最大化的价格集合［1］。实践证明，动态定价能够显著提高航空运输企业的收益［2］。相比于客运来讲，航空货运的动态定价是个尚未受到足够关注的领域。目前我国航空货运定价通常采用单一的定价策略，呆板且不符合市场经济规律。随着各大航空公司对货运重视程度的提高，航空货运动态定价作为提升盈利能力的有效工具，需要加以研究［3］。

PAK 和DEKKER［4］利用多维背包思想构建了多航段时间离散型的航空货运定价模型。HAN等［5］运用马尔可夫模型，推导了单航段的货运bid－price 控制策略。XIAO 和YANG［6］研究了适用于货运收益管理的两维容量属性下易逝品的收益管理问题。赵桂红［7］，张辉［8］，桂云苗等［9］探讨了航空货运的定价体系。鞠学见和罗利［10］分析了竞争与合谋情况下的航空货运服务定价策略。雷丽彩和周晶［11］在考虑风险规避货运代理商的情况下分析了航空公司的最优定价。王晓立和马士华［12］研究了航空货运市场运力分配和定价的协调问题。周寅艳［13］建立了竞争市场环境下货物多级运价动态模型。上述研究没有考虑需求规律的不确定性对定价的影响。由于航空货运行业的特殊性，货运市场需求弹性大，波动性强，需求函数参数的估计不完全准确，这增加了定价决策的风险。笔者在前人研究的基础上，引入相对熵理论构建航空货运动态定价鲁棒优化模型，旨在增加航空公司收益的同时降低公司定价决策的风险，为航空货运销售人员提供理论参考。

1 问题描述、符号说明及假设条件

1.1 问题描述

(1)航空货运的基本规定。不管货物使用直飞航班还是转机航班，收取货主的运费相同［14］。

(2)虽然国际航协规定了会员航空公司之间的货运收费标准，但现在大部分航空公司基本上是销售人员凭自己的判断和经验与货主议价，这是笔者定价策略的可行性依据。

(3)航空公司通常在已有的客运航线网络上运用飞机腹舱装载货物，航班特定的容量决定其短期运价水平。不同城市对市场的需求函数弹性不同。

(4)每年初航空公司以“定价包量”的方式与代理人签订协议，因此在短期销售中这部分收益固定。笔者以实际销售过程中航空公司去除协议舱位后的自由销售行为为主体进行研究。

1.2 符号说明

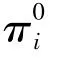
1.3 假设条件

(2)各类货物流之间需求相互独立，但每类货物流各周期的随机项可能相关。

(3)公司收益以货物质量为计费单位。

(4)每类货物的单位费率由行业规定的价格限制，第g 类货物费率的上限和下限分别为pu(g)，pd(g)。

(5)在作出价格决策时，自然与决策者构成二人零和非合作博弈，即自然总是选择使收益最小的分布。

2 模型

2.1 动态定价名义模型

在不考虑需求函数随机项的参考分布与实际分布存在偏差的情况下，航空公司的收益模型［15］如下:

目标函数表示货物的最大期望收益;式(2)表示货物价格在行业限制范围内;式(3)和式(4)表示航节j 的质量约束;式(5)和式(6)表示航节j 的体积约束;式(7)表示销售量非负，小于需求量。

2.2 相对熵约束

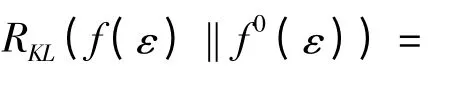
2.3 动态定价鲁棒优化模型

假设实际的概率密度π∈{π|RKL(π‖π0)≤γ}总在集合内选择使公司的期望收益最小的分布，运用最大最小定理［17］，建立鲁棒优化模型如下:

将相对熵约束用拉格朗日乘子αi相乘后加到目标函数中，将模型化为惩罚函数形式:

3 求解方法

3.1 内部求极值

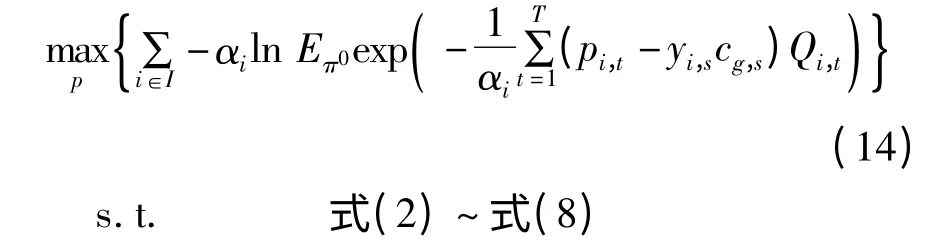
3.2 近似处理

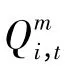
3.3 人工蜂群算法

人工蜂群算法ABC(artificial bee colony algorithm)由KARABOGA 在2005 年提出，是一种模仿蜂群自组织的群体智能随机搜索算法。该算法简单，鲁棒性强，经过改进，可以较好地解决高维的非线性优化问题［18］。

人工蜂群算法的计算步骤如下:

(2)蜂群初始化。运用正交设计法［19］初始化搜索域，在范围内计算每个食物源的适应度并进行选择。

(3)根据适应度划分蜂群为被雇用蜂和旁观蜂两类，记录目前的最佳适应度和解集。

(4)旁观蜂群根据被雇用蜂的适应度选择性地跟随，寻找更好的解。

(5)在规定的跟随迭代次数内旁观蜂若找到更好的解，更新最佳适应度和解集，旁观蜂转换为被雇用蜂，转到步骤(3);若没有更新或迭代次数已满，蜜蜂转换为探索蜂，转到步骤(2)。

(6)重复步骤(3)～步骤(5)直到满足终止条件。

4 算例分析

假设有3 类货物，对应的单位质量体积以及单位费率上下限制如表1 所示。

表1 货物单位质量体积和价格限制

航空公司有两条航线:一条南京—郑州—重庆的中转航线，一条南京—重庆的直达航线，航节对应的质量和体积限制如表2 所示。货物运输成本如表3 所示。

表2 航节质量和体积限制

表3 货物运输成本 元/kg

以需求函数确定形式为线性减函数为例，有di，t=ai，t－bi，tpi，t，公司经调查得到的ai，t，bi，t估计值如表4 所示。

表4 需求反应函数系数

为方便讨论，令随机变量δi，t的参考分布均相同，为δi，t～U(0.8，1.2)，令α1=α2=… =αI=α分别为5，50，100，讨论如下悲观情况:

(1)随机需求函数形式为di，t=ai，tδi，t－bi，t·pi，t，实际的总需求量比估计的总需求量少。δi，t～U(0.6，1.0)和δi，t～U(0.1，1.1)下的收益比较如表5 所示;

(2)随机需求函数形式为di，t=ai，t－bi，tδi，t·pi，t，消费者对价格的敏感程度实际值比估计值更高。δi，t～U(1.0，1.4)和δi，t～U(0.9，1.9)下的收益比较如表6 所示。

表5 需求函数形式为di，t =ai，tδi，t－bi，tpi，t价格决策收益比较

表6 需求函数形式为di，t =ai，t－bi，tδi，tpi，t价格决策收益比较

从表5 和表6 可知，在需求函数参数的实际分布较估计水平更不利的情况下，鲁棒优化后的价格决策更优。随着αi的降低，货运收益期望上升，同时波动范围逐渐缩小，最优收益水平和最差收益水平的取值均向右移动。

5 结论

笔者从航空公司角度，在考虑货物质量和体积二维约束的情况下，基于相对熵建立了航空货运动态定价的鲁棒优化模型。在实际需求较估计水平更不利的情况下，该模型能在增大收益的同时降低决策的风险。但是这种随机鲁棒优化方式对货运需求的参考分布存在一定依赖性。当实际需求情况严重偏离参考情况时，价格策略不能单单靠改变信心系数来制定，而应该实时更新参考分布。如何根据实际情况更新参考分布，以及怎样根据不同的情况选取合理的αi值，是需要深入研究的问题。

［1］ 罗伯特·菲利普斯.定价与收益优化［M］.陈旭，慕银平，译.北京:中国财政经济出版社，2008:32－98.

［2］ 熊中楷.动态定价新视角［M］.北京:科学出版社，2010:65－142.

［3］ PETERSEN J. Air freight industry－white paper［J］.Management，2007(1):1－46.

［4］ PAK K，DEKKER R. Cargo revenue management:bid－ prices for a 0－1 multi knapsack problem［R］.［S.l.］:ERIM Report ERS－2004－055－LIS，2004.

［5］ HAN D L，TANG L C，HUANG H C.A Markov model for single－leg air cargo revenue management under a bid－price policy［J］.European Journal of Operational Research，2010(3):800－811.

［6］ XIAO B C，YANG W.A revenue management model for products with two capacity dimensions［J］. European Journal of Operational Research，2010(2):412－421.

［7］ 赵桂红.航空货运定价策略探讨［J］.中国民航学院学报，2003(5):7－12.

［8］ 张辉.民航货物运输定价策略浅谈［J］. 空运商务，2006(24):15－16.

［9］ 桂云苗，朱金福. 航空货运时间相关定价模型研究［J］.商业时代，2007(9):66－67.

［10］鞠学见，罗利. 航空货运公司定价策略博弈分析［J］.技术与市场，2009(1):32－34.

［11］雷丽彩，周晶. 风险规避下的航空货运期权定价Stackelberg 博弈模型［J］. 系统工程理论与实践，2010(2):264－271.

［12］王晓立，马士华.航空货运市场运力分配及定价的协调问题研究［J］.工业工程与管理，2010(1):65－68.

［13］周寅艳. 航空公司货运动态定价与容量控制研究［D］.南京:南京航空航天大学图书馆，2012.

［14］杨思梁.航空公司的经营与管理［M］.北京:中国民航出版社，2008:15－90.

［15］李根道.模型不确定下的收益管理动态定价策略研究［D］.重庆:重庆大学图书馆，2009.

［16］ LIMA E B，SHANTHIKUMAR J G. Relative entropy，exponential utility，and robust dynamic dricing［J］.Operations Research，2007，55(2):198－214.

［17］HANSEN L P.Robustness［M］.［S.l.］:Princeton University Press，2007:51－120.

［18］拓守恒.一种求解高维约束优化问题的人工蜂群算法［J］.计算机应用研究，2012(3):937－940.

［19］LEUNG Y W，WANG Y P.An orthogonal genetic algorithm with quantization for global numerical optimization［J］. IEEE Transactions on Evolutionary Compuation，2001，5(1):41－53.