基于蒙特卡洛技术时变Copula 的比较

2013-12-23昌春艳

武汉理工大学学报（信息与管理工程版） 2013年3期

刘娟，王沁，刘军，昌春艳

(1.西南交通大学数学学院，四川成都610031;2.西南交通大学经济管理学院，四川成都610031)

Copula 函数，即为连接函数，它是把联合分布函数与边缘分布函数连接在一起的桥梁。2001年，PATTON 首先提出时变Copula 模型，该模型利用类似ARMA(1，10)的模型描述了二元正态Copula 模型的参数随时间的演变过程［1］。在PATTON 的基础上，韦艳华等建立了Copula－GARCH 模型［2］，比较了常相关、时变相关的二元正态Copula 模型，其结果表明金融时间序列具有明显的时变性。龚金国等采用经验分布－局部极大似然估计法，估计了时变Copula 模型的参数，并用广义伪对数似然函数检验其时变性，证实了该方法的优越性和稳健性［3］。文献［4］利用Spearman ρ 建立时变Copula 模型，以FGM－Copula 为例，表明了从Spearman ρ 角度出发建立的时变模型能较好地诠释金融变量之间的相依机制。

建立时变Copula 模型的方法通常有3 种，分别是从线性相关系数、Kendall τ、尾部相关系数出发建立时变Copula 模型［5－6］。由于变量之间发生非线性单调变换时，其线性相关系数将会发生变化，因此，从线性相关系数的角度建立的时变Copula 模型存在不足，不能很好地描述变量之间非线性的相依机制。对于从Kendall τ、尾部相关系数出发建立的时变Copula 模型的优劣性，尚没有文献进行讨论，笔者从Kendall τ、尾部相关系数出发建立时变Copula 模型，并分析和讨论了其优劣性。

1 Kendall τ 与尾部相关系数

定义1 设(X1，Y1)，(X2，Y2)为独立同分布的二维随机变量，则Kendall τ 为［7］:

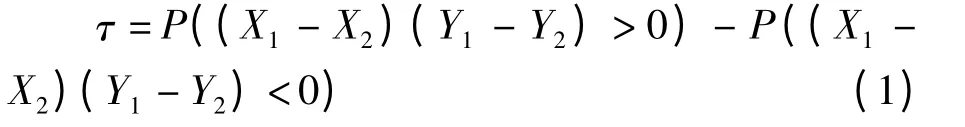
其中:(X1－X2)(Y1－Y2)＞0 说明两个变量的变化方向一致，是和谐的;(X1－X2)(Y1－Y2)＜0 说明两个变量的变化是反向一致的，是不和谐的。

τ=1 表示X 的变化与Y 的变化完全一致，是正相关的;τ=－1 表示X 的变化与Y 的反向变化完全一致，是负相关的;τ =0 表示X 的变化与Y的变化一半是一致的，一半是反相一致的，故不能判断其相关性。

因此，Kendall τ 反映了变化一致与否的程度，是一个一致性指标，也是一个全局变量。

根据Sklar 定理［8］，随机变量(X，Y)的联合分布函数H(x，y)可以表示为一个Copula 函数和其边缘分布函数的复合函数，即:

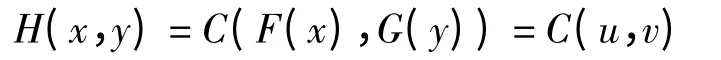
其中:C(·，·)为二元Copula 函数;F(x)为X的分布函数;G(y)为Y 的分布函数;u=F(x)，v=G(y)。

从Sklar 定理可以看出，Copula 实际上是一个将联合分布函数和边缘分布函数连接起来的函数，它能捕捉两个变量之间的相依机制、相依关系［9］。

由Copula 函数可知，(X，Y)的Kendall τ 可以表示为:

其中，Cθ(u，v)为总体参数，是θ 的一族Copula 函数。

若二重积分可以直接积分且有封闭的表达式，那么，Kendall τ 与总体参数θ 存在一一对应关系。则基于这种一一对应的关系，利用Kendall τ的统计量来估计总体参数θ，建立总体参数θ 的时变演变方程。

目前，在金融风险分析中，除了利用Kendall τ指标来刻画变量之间的相关关系以外，还有很多学者利用变量之间的尾部相关系数来分析金融市场中的风险。尾部相关系数表示当一个观测变量出现为极值时另一个变量也会出现极值的概率。它可以直观地反映一支股票价格的暴跌是否会引发另一支股票价格的暴跌，或者一个金融市场的大波动是否会引发另一个金融市场的大波动［10］。

定义2 假定X、Y 为两个连续的随机变量，具有边缘分布F(·)G(·)，其Copula 函数为C(·，·)，则上尾相关系数为:

下尾相关系数为:

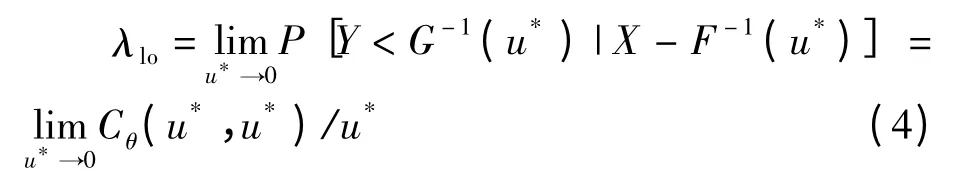
若这类极限存在，则上尾相关系数、下尾相关系数与总体参数θ 一一对应。则基于这种一一对应的关系，利用尾相关系数的统计量来估计总体参数θ，建立总体参数θ 的动态演变方程。

由于Copula 函数在非线性单调变换下保持不变，因此，Kendall τ 和尾部相关系数在非线性单调变化下也会保持不变，且与Copula 函数的总体参数θ 是一一对应的。因此，从Kendall τ 和尾部相关系数构建时变Copula 模型是可行的，并且相比从线性相关系数出发构建的时变Copula 模型，更具有优越性。

尾部相关系数是指当一个变量出现极值时另一个变量也出现极值的概率，它是一个极限，一个局部变量，其统计量仍然可以利用频数来构造，但是频数依赖于u*的一个小邻域，因此，从尾部相关系数构建时变Copula 模型在理论上有缺陷，劣于从Kendall τ 构建时变Copula 模型。

综上可知，虽然从Kendall τ 和尾部相关系数都可以构建时变Copula 模型，但是从Kendall τ 构建时变Copula 模型会更具有优越性。下面以Clayton Copula 为例来验证两种时变模型的优劣性。

对于Clayton Copula 函数，其Kendall τ 和下尾相关系数与总体参数θ 存在一一对应关系，故Kendall τ 和下尾相关系数可以建立其时变的Copula 函数。

虽然笔者是以Clayton Copula 函数为例，但是Kendall τ 和尾部相关系数与Copula 函数的总体参数θ 是一一对应的，用Kendall τ 和尾部相关系数来构建其时变性都是可行的。

2 蒙特卡洛技术与时变Copula 模型建立

笔者以Clayton Copula 函数为例，假定参数的AR(1)模型，利用蒙特卡洛模拟技术仿真得到样本的数据来建立两类时变Copula 模型。

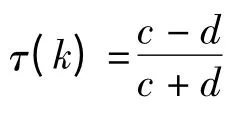
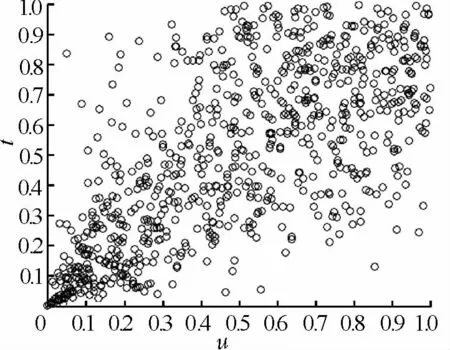
图1 Clayton Copula 模型的散点图

根据样本数据，计算所得的时变Kendall τ，时变下尾相关系数的曲线图如图2 所示。

图2 Kendall τ、下尾相关系数时变图

(3)计算总体参数，建立时变Clayton Copula模型。根据Kendall τ、尾部相关系数与Copula 的总体参数θ 之间的一一对应关系得到Copula 的总体参数θ 的估计值θ1(i)，θ2(i)，图3 为θ1(i)，θ2(i)与θ(i)的线图。

图3 从Kendall τ 角度，尾相关角度估计的θ 数据与样本数据的线图

由图3 可以知道θ 的样本数据很快收敛到1.87，从Kendall τ 角度得到的时变Copula 模型的参数估计值θ1在第200 个数据后围绕着1.87 小范围波动，从尾相关系数角度得到的时变Copula模型的参数估计值θ2与1.87 之间的差异要比θ1与1.87 的差异大。因此，从Kendall τ 出发比从尾相关系数出发得到的结果要好，更能反映变量之间的相依机制。

图4、图5 分别为θ1，θ2的自相关函数界面图。由图4、图5 可以得出，自相关函数均有拖尾性，偏相关函数一步截尾，故用AR(1)模型对序列θ1，θ2进行拟合，得到它的估计方程为:

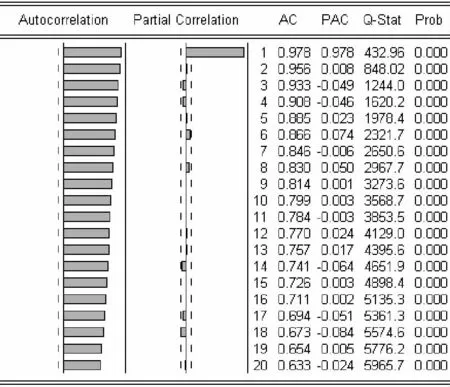
图4 Kendall τ 得到的θ1 自相关函数界面图

图5 下尾相关系数得到的θ2 自相关函数界面图

θ1(t)=1.950 778 +0.982 528θ1(t－1)

θ2(t)=2.092 001 +0.904 095θ2(t－1)

3 两种时变Copula 模型的比较

(1)时变Copula 模型参数估计。从Kendall τ、尾相关系数得到的θ1，θ2的AR(1)模型的估计结果如表1 所示。

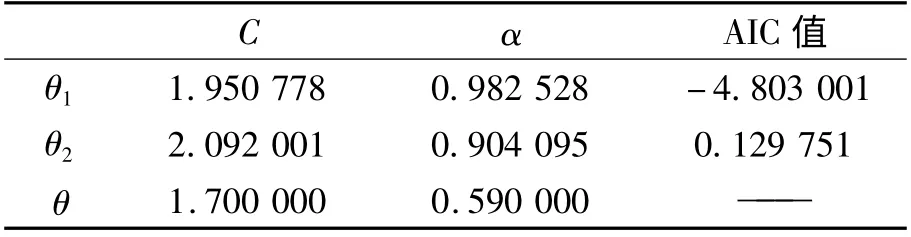
表1 θ1、θ2 的AR(1)模型参数估计结果

表1 列出了θ1，θ2的AR(1)模型的参数估计结果，θ1的AR(1)模型中常数项比θ2的更接近θ的AR(1)模型的常数项，θ1的AR(1)模型的AIC值比θ2的AR(1)模型的AIC 要低，说明θ1的AR(1)模型对数据的拟合比θ2的AR(1)模型要好，这反映了从Kendall τ 建立的时变Copula 模型要优于从尾相关建立的时变Copula 模型。

表2 两种不同情况下的拟合优度检验

由表2 可知，从Kendall τ 角度建立的时变Copula 模型的预测值与真实值之间的偏差要比从尾相关角度建立的时变Copula 模型的预测值与真实值的偏差小，且二者的差异非常大，而从Kendall τ 的角度建立的时变Copula 模型的预测值与真实值的绝对值平均误差和均方误差的平方根均比从尾相关角度建立的时变Copula 模型的预测值与真实值的要小。因此，从实证的角度验证了从Kendall τ 角度建立的时变Copula 更适合金融数据的相依机制。