二元相依随机变量和的精确大偏差

杨少华，于海芳，华志强

（1.阜阳师范学院 数学与计算科学学院，安徽 阜阳 236037；2.朝阳师范高等专科学校 数学计算机系，辽宁 朝阳 122000；3.内蒙古民族大学 数学学院，内蒙古 通辽 028043）

0 引言及预备知识

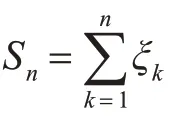
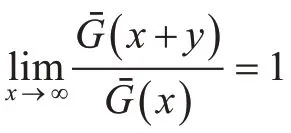
定义2［4］称随机变量序列{ξn，n ≥1} 为二元相依的，如果对任意的i，j=1，2，…，i ≠j，有

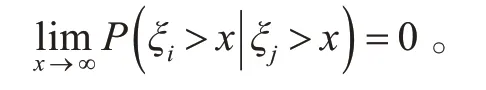
1 非随机和的精确大偏差

定理1 设{ξk，k ≥1} 为一个二元相依的随机变量序列，其分布为Gi∈L，存在有限的数学期望μ，且Gi(i=1，2，… )满足假设条件1：对某个T ＞0，存在x ≥T ，一致地有

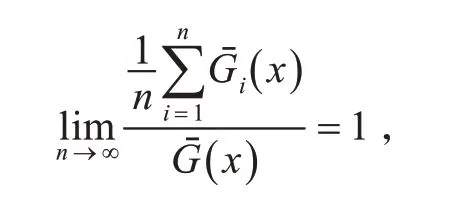
则对任意常数γ ＞0 ，当n →∞时，对x ≥γn ，一致地有

证明 由于

由定义2 知，当x 充分大时，存在ε1=ε1( x )，使得

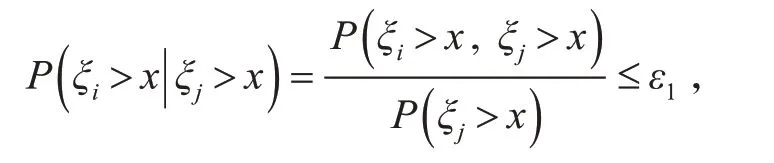
又由假设条件1 知，当n 充分大时，存在充分小的ε2=ε2( n )和ε3=ε3( n )，使得

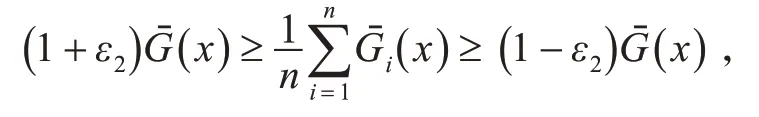
从而有

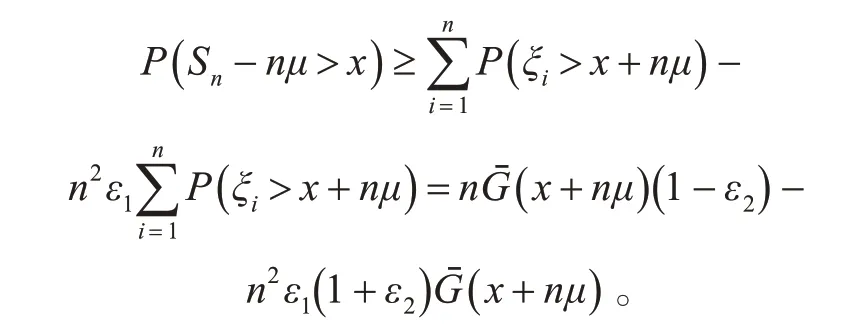
当固定n 时，令ε1→0，ε2→0，可得

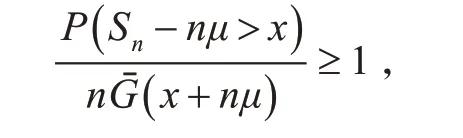
故当n →∞时，对x ≥γn，一致地有

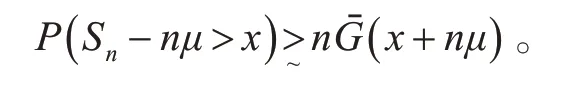
2 随机和的精确大偏差

由文献［2］，给出假设条件2：当t →∞时，对于任意的δ ＞0 和任意小的ε ＞0，有

定理2 设{ξk，k ≥1} 为一个满足定理1 的随机变量序列，且独立于取非负整数值的随机过程{Nt，t ≥0} 。假设{Nt，t ≥0} 满足假设条件2，则对任意常数γ ＞0 ，当t →∞时，对x ≥γλt，一致地有

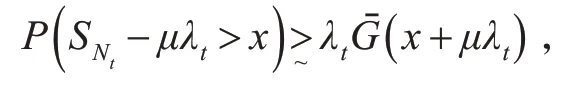
且当t →∞时，对x ≥γλt，一致地有

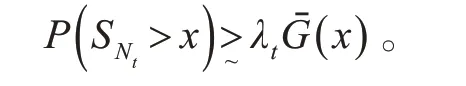
证明 对任意的0 ＜δ ＜1，有

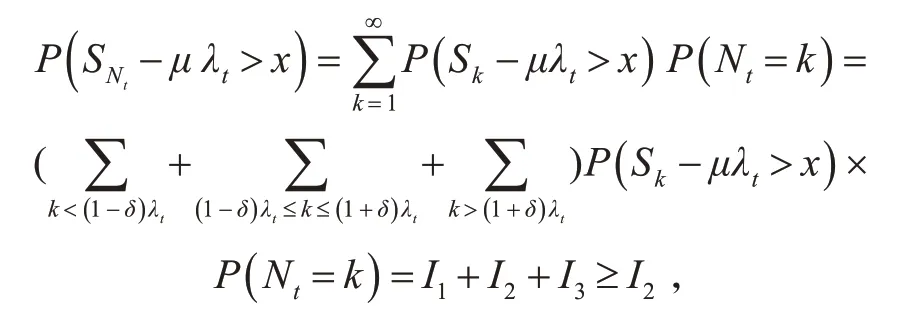
以下计算I2：

由假设条件1，得到如下的渐近关系：

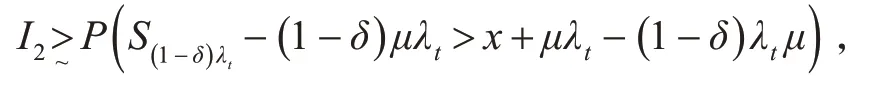
又由定理1 可得

由（1）式可导出

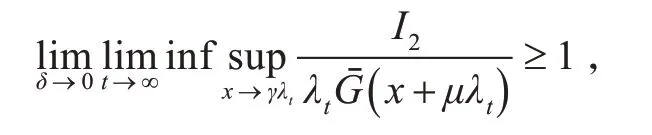
故对任意常数γ ＞0 ，当t →∞时，对x ≥γ λt，一致地有

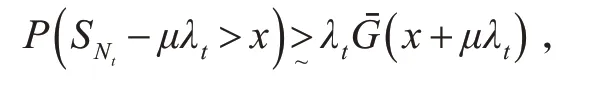
并且当t →∞时，对x ≥γ λt，一致地有

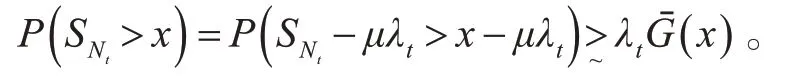
［1］ Klüppelberg C，Mikosch T. Large deviations of heavy－tailed random sums with applications in insurance and finance［J］. Journal of Applied Probability，1997，34（2）：293－308.

［2］ Ng K W，Tang Q，Yang J A，et al. Precise large deviations for sums of random variables with consistently varying tails［J］. Journal of Applied Probability，2004，41（1）：93－107.

［3］ Liu L. Precise large deviation for dependent random variables with heavy tails［J］. Statistics & Probability Letters，2009，79（9）：1290－1298.

［4］ Yang Y，Wang K. Uniform asymptotics for the finite－time and infinite－time ruin probabilities in a dependent risk model with constant interest rate and heavy－tailed claims［J］. Lithuanian Mathematical Journal，2012，52（1）：111－121.

［5］ Konstantinides D G，Loukissas F. Precise large deviations for sums of negatively dependent random variables with common long－tailed distributions［J］. Communications in Statistics－Theory and Methods，2011，40（19）：3663－3671.

［6］ 华志强，姜晓威.带延拓负上限相关的随机变量和的精确大偏差［J］. 北华大学学报：自然科学版，2012，13（4）：398－400.