统计过程控制在钼粉生产中的应用

石大伟

(金堆城钼业股份有限公司金属公司，陕西 西安 710077)

0 引 言

钼粉作为钼金属初级产品，对后续金属产品的质量起着至关重要的作用，要生产出优质的钼金属产品，先决条件就是要有优质的钼粉。目前金堆城钼业股份有限公司产品质量主要是通过现场检验和成品检验来发现不合格品，这种事后检查方法忽视了对制造过程的控制和改进，既造成人力、材料及时间的浪费，同时对产品的整体质量造成影响。如何降低不合格品率，提高产品质量，确保产品在生产过程中有效控制，并使加工能力不断提高，这是一个十分重要的问题。本文探讨SPC 在钼粉生产中的应用，以钼粉粒度指标为例，对加工过程进行管理和控制，利用控制图及时发现过程的不稳定性，达到过程预警功能，使过程不断改进，过程能力不断提高。

1 SPC 原理

统计过程控制(Statistical Process Control，SPC)是一种借助数理统计方法的过程控制工具。应用SPC 对质量数据进行统计、分析，建立分析用控制图，并计算过程能力，再将分析用控制图转化为生产过程控制用过程图。通过数据采集，并在控制图中打点的方法，利用判异准则，从质量数据的排列分析生产过程是否稳定。从而区分出生产过程中产品质量的正常波动与异常波动，以便对过程的异常及时提出预警，提醒管理人员采取措施消除异常，恢复过程的稳定性，从而提高产品质量。

1.1 质量控制图的结构

控制图是对过程质量特性值进行测定、记录、评估，从而监察过程是否处于控制状态的一种用统计方法设计的图［1］。图上有中心线(CL)、上控制线(UCL)和下控制线(LCL)，并有按时间顺序抽取的样本统计量数值的描点序列，参见图1。UCL 与LCL 统称控制线。若控制图中的描点落在UCL 与LCL 之外或描点在UCL 与LCL 之间的排列不随机(有规律或某些缺陷)，则表明过程异常。控制图有一个很大的优点，即在图中将所描绘的点子与控制界限相比较，从而能够直观地看到产品或服务质量的变化。

质量控制图理论认为，产品指标数据作为观测值存在变异性是不可避免的，这个变异性是由随机抽取的或可定的因素引起的［2］。如果一个因素造成的影响显著、不寻常且能在生产过程排除，则认为它是可定的，这样的原因包括设备老化、工艺变更、作业人员变化及技能水平等。如果造成的影响小而不可控制，则认为它是随机的。而质量控制图把反映生产过程的统计量，如移动极差，作为时间的函数进行标绘，是了解和减少生产过程变异性的一个重要工具［2］。

1.2 质量控制图上的模式分析

对控制图上观测点异常模式的分析，在确认可定因素上常常是有用的。异常模式如周而复始或连续接近一个控制限的数值，会指示存在非随机变异。而许多判异准则可以发出警告帮助我们去寻找可定因素的存在，为了讨论判异准则的方便，可把控制图分成图1 所示的若干区域。控制图上下两侧分隔诸区的虚线，在中心线(CL)和上控制线(UCL)及下控制线(LCL)之间是等距的。

判异准则有点出界和界内点排列不随机两类［3］。在国标GB/T 4091－2001 中规定了8 种判异准则:

准则1:一点落在A 区以外。

准则2:连续9 点落在中心线同一侧。

准则3:连续6 点递增或递减。

准则4:连续14 点相邻点上下交替。

准则5:连续3 点中有两点落在中心线同一侧的B 区以外。

准则6:连续5 点中有4 点落在中心线同一侧的C 区以外。

准则7:连续15 点在C 区中心线上下。

准则8:连续8 点在中心线两侧，但无一在C 区中。

2 SPC 在钼粉生产中的实际应用

2.1 选择控制点

钼粉生产过程是一个还原过程，其主要控制指标有:

化学指标:化学指标的控制主要取决于原料的指标，在钼粉的生产过程中，只要控制好设备、料舟以及环境因素，化学指标基本上不会发生太大的变化。

物理指标:在钼粉的物理指标中，粒度会随着生产工艺的不同产生较大的变化，且粒度指标对后续的加工过程是非常重要的。

在使用控制图时应该选择能够真正代表过程的主要指标作为控制对象，因此，本文选择钼粉的物理指标粒度为控制变量，阐述SPC 方法的实际应用。

2.2 建立分析用控制图

表1 计量控制图系数表

表2 中给出了连续10 批钼粉的粒度值，希望将钼粉粒度指标控制在4.5 以下。由于发现单批内抽样变差可以忽略，因此决定对每批只抽取一个观测值，并以连续各批的移动极差作为设置控制限的基础。

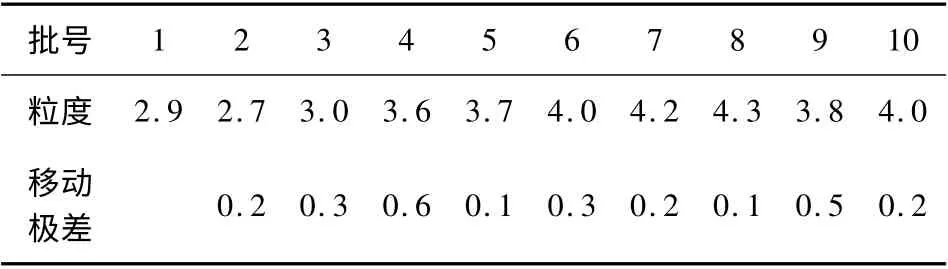
表2 钼粉粒度值及极差值

X=3.62

Rs=0.28

移动极差(Rs)控制图:

CLRs=Rs=0.28

UCLRs=D4Rs=3.267 ×0.28 =0.91

LCLRs=D3Rs=0 ×0.28

系数D3、D4的值由计量控制图系数表1 中按n=2查得，根据以上计算，绘制移动极差控制图。

由于该移动极差已经呈现出统计控制状态(如图1 所示)，于是可以进行单值控制图的绘制。

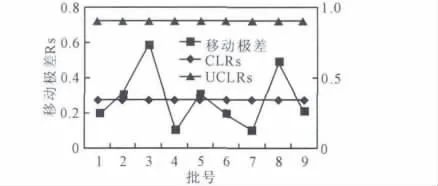
图1 表1 数据的移动极差Rs 控制图

单值X 控制图:

CLx= X=3.53

UCLx= X+E2R=3.62 +2.66 ×0.28 =4.36

LCLx= X－E2R=3.62－2.66 ×0.2 =2.88

表1 数据的单值X 控制图见图1。

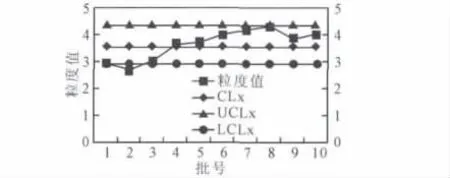
图2 表1 数据的单值X 控制图

由图2 可以看出，已经有连续7 点落在中心线的同一侧，判断过程异常。

2.3 对控制图进行分析

利用对控制图的分析，及时发现变异，及时寻找造成过程异常的根本原因，采取必要的措施，最终使生产过程稳定。这是一个PDCA 循环过程。当控制持续一段时间后，工序状态必然会发生变化，如:设备老化、工艺变更、作业人员变化及技能水平等，因此，需要重新进行计算，验证控制状态的稳定性。

3 结 论

应用统计技术对钼粉生产过程的关键技术参数进行分析和监控，及时发现异常，改善加工过程，提高过程能力，达到改善钼粉性能的目的。所以在目前对钼粉性能日益提高的要求下，统计过程控制是一种很好的控制产品质量的方法。

［1］ 陈俊芳，黄 培，张爱文.质量管理学［M］.北京:中国标准出版社，2004.

［2］ 龚国华，龚益鸣. 生产与运营管理［M］. 上海:复旦大学出版社，1998.

［3］ 董文尧，于伟利，陈岩.质量管理学［M］.北京:清华大学出版社，2006.