基于元胞小生境遗传算法的物流配送路径优化*

朱大林，詹 腾，张 屹，刘 铮

(三峡大学 机械与材料学院，宜昌 443002)

0 引言

近年来，随着经济和社会的高速迅猛发展，不断地促进了物流产业的快速发展，现在物流业已经成为我国经济发展中的重要领域。现代物流贯穿于各个领域，包括生产制造领域、消费循环、产品配送等，它已经成为企业降低生产经营成本，提高市场竞争力的重要途径。作为物流配送优化中非常关键的一环，车辆路径问题(Vehicle Routing Problem，VRP)的研究受到了人们的广泛的关注。

带有时间窗约束的车辆路径问题(Vehicle Routing Problem with Time Window，VRPTW)是一种带有约束条件的VRP 问题，即对车辆到达的时间有时间范围的要求，车辆必须在该时间范围内到达服务点，否则将会影响顾客对服务的满意度，对于该问题不仅要计算车辆的行驶成本，而且要考虑早到客户点需要的等待时间或晚到要付出惩罚的成本，因此该问题较一般的VRP 问题更为复杂，是一个NP 疑难问题［1］。因为VRPTW 问题更贴近现实实际应用，所以得到了深入的研究，目前常用的解决VRPTW 问题的方法有:禁忌搜索算法［2-3］、模拟退火算法［4］、粒子群算法［5］、免疫算法［6］和一些改进的遗传算法［7-9］等，这些方法用于解决VRPTW 问题已经取得了一些较好的研究成果。

元胞遗传算法(Cellular Genetic Algorithm，cGAs)［10］是将元胞自动机机理和遗传算法相互结合得到的一种新型的进化算法，其特点在于将种群分布在一种特殊的拓扑结构中，一般采用二维环形结构，且种群的每个个体仅限于和其规定的邻居之间进行遗传操作，这种结构赋予该算法一个细晶度并行功能［11］，并且有较好的全局搜索和局部搜索能力。鉴于此，本文在经典元胞遗传算法的基础之上，加入小生境技术，提出了一种元胞小生境遗传算法(Cellular Niche Genetic Algorithm CNGA)，进一步改进算法种群多样性和跳出局部最优解的能力。将此算法引入VRPTW 问题的求解当中，并针对该问题提出一种改进的交叉算子，以图获得更好的求解效果。

1 物流配送路径优化模型

假设某公司有M 个配送中心，N 个货物需求点，VRP 的任务就是将货物从M 配送中心送到N 个货物需求点上，既要满足需求点货物量的要求，又要使配送成本最小。将各需求点的任务分配给距它最近的配送中心，每个配送中心需负责将自己区域的货物送达到，这样多配送中心将转化为单配送中心问题，以下为单配送中心的数学模型。

假设某一配送中心拥有载重量为Gt 的车辆m辆，需要对n 个客户点输送货物，即该问题为对n 个点进行排列，使其满足配送需求且使得总的配送成本最小。

1.1 基本假设

(1)每个配送中心所服务的客户点和客户需求量已知;

(2)每个客户点和配送中心的距离以及每个客户点之间的距离已知;

(3)每个客户点只由一辆车服务一次;

(4)车辆每到一个客户点只有卸货时间而无装货时间;

(5)每辆车必须从配送中心出发，完成任务再返回配送中心;

(6)配送中心所有车辆种类单一，且额定载荷量已知;

(7)车辆的平均行驶速度已知。

1.2 约束条件

(1)每辆车的载货重量不能超过其额定载荷量;

(2)时间窗约束:分为硬时间窗和软时间窗。对每个服务点i 的任务，都要求在一定的时间范围［STi，ETi］内完成，其中STi表示任务允许开始的最早时间，ETi表示任务允许的最迟开始时间。如果车辆在STi之前到达，则车辆在任务点处要等待;如果到达时间晚于ETi，任务就会被延迟执行。以Ti表示车辆到达任务点的时间，如果是硬时间窗，则Ti必须满足STi≤Ti≤ETi;如果是软时间窗，则早于STi或者晚于ETi时将要受到惩罚。

(3)运输过程的单向性;每一辆车必须以配送中心作为起始点，沿路径为客户服务，要求每个客户只能由给定的车辆服务，且每辆车服务完后不能又折返回上一个客户点，是单向性的路线行驶，最后每辆车终点都是配送中心。

1.3 数学模型

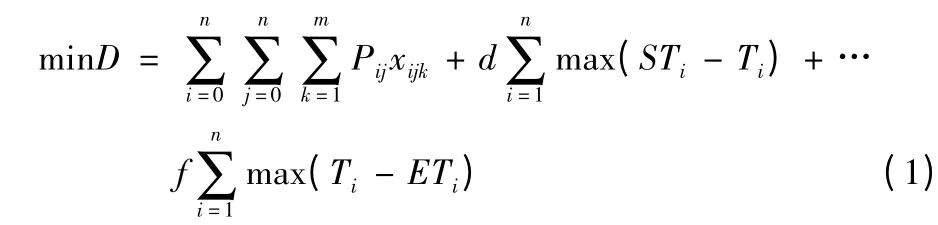
约束条件:

式中:D 表示车辆行驶的总距离;i 为客户编号;j 为客户编号;n 为客户数量;k 表示第k 辆车(k = 1，2，…，m);qi为客户i 的货物需求量;G 为车辆额定载荷量;Pij为从客户i 到客户j 的运输成本;Ti为车辆到达客户i 的时间;d、f 为参数。

上述式(1)表示为总的运输成本，包括车辆的运输成本和违反时间窗约定的惩罚成本;式(2)(3)表示决策变量;式(4)表示每辆车不能超过其额定载荷;式(5)表示每辆车的起始地点都为配送中心;式(6)每一个客户只能被一辆车服务;式(7)表示每辆车服务完后都必须返回到起始点配送中心;式(8)(9)表示两个决策变量之间的关系。

2 元胞小生境遗传算法

为了对上述VRPTW 优化模型进行优化计算，提出了一种新的元胞遗传算法CNGA。CNGA 是在经典元胞遗传算法的基础上引入小生境技术，使算法能更好地保持种群多样性，避免过早出现“早熟”现象。

2.1 元胞遗传算法

元胞遗传算法［1］是将元胞自动机作用机理和遗传算法有机的结合，种群中的个体按照一定的拓扑结构分布，一般情况下采用二维结构，如下图1 中所示，每个个体有相同的邻居数，且每个个体仅限于和邻居个体之间进行遗传操作，这在一定程度上降低了算法的选择压力，使得元胞遗传算法成为解决复杂问题的一种有效方法。

图1 种群分布示意图

经典元胞遗传算法的基本步骤如图2 所示。

图2 经典元胞遗传算法

图2 为步骤解析:①将种群分布在二维环形拓扑结构中;②在邻居结构中选择一个元胞个体作为父代;③将选择出来的邻居元胞和中心元胞进行交叉，变异操作;④产生新的个体;⑤如果新的个体优于中心元胞，在将中心元胞替换，否则，不替换;⑥如果generation ＜MAXGEN，返回至步骤②;⑦输出当前最优解。

2.2 小生境技术

本文采用基于排挤机制的小生境策略。首先假设种群(M + N)的组成是父代中优秀的N 个个体和使用精英保留策略子代种群M 个个体，按照下式求出每两个个体Ci和Cj之间的海明距离:

小生境过程为:首先对种群中两两个体进行比较其海明距离，如果这个距离d(i，j)在预先设置的距离L 之内，则对其中的适应度较低地个体施加一个比较大的罚函数，使其适应度大大地降低，因此其中相对较差的个体就很大可能在进化的过程中被淘汰掉。随着排挤过程的不断进行，群体中的个体将会被逐渐分类，从而生成了许多小的生存环境，维持了种群的多样性，使得解空间分布均匀。小生境技术能够指引种群的发展趋势，不断将其指引到更好地方向，有利于全局搜索。

2.3 算法步骤

本文中采用二维环形拓扑结构，其种群结构使用Moore 形(如图1 中b 所示)，其种群更新方式为同步策略，表1 为CNGA 的伪代码。

表1 CNGA 的伪代码

首先产生初始种群，将初始种群分布于二维环形结构中。随后使用轮盘赌选择从中心元胞的邻居中选择出一个个体，进行交叉操作，产生新的个体，再对新的个体进行变异操作。随后进行替换操作，对变异后产生的新个体与中心元胞进行比较，若新个体优于中心元胞，将此个体替换中心元胞，否则不替换，保留中心元胞。将新生的子代种群个体，与父代中记忆的N 个个体合并在一起，组合成一个N + M 个个体的新种群，然后计算个体的适应度值并排列，根据排序选择相邻若干个个体进入一个小生境。对适应度低的个体进行施加一个比较大的罚函数，降低其适应度值。保存优秀的前M 个个体作为下一代种群，其前N 个个体作为下一代种群的父代小生境个体。

3 VRPTW 问题的实例求解与分析

3.1 求解步骤

Step1:随机生成初始种群。采用自然数编码生成初始种群，编码个体即表示为客户的顺序排列，对于个体，在其首尾加入“0”，再在其个体中间位置随机的插入n－1 个“0”，n 代表运输车辆的数目，如图3所示表示该运输任务由三辆车完成8 个客户，其中每辆车的运输路径为:配送中心→客户(7 →4 →1)→配送中心;配送中心→客户(8 →3)→配送中心;配送中心→客户(5 →2 →6)→配送中心。

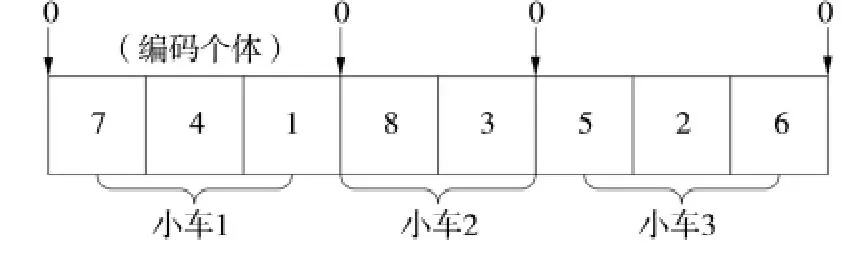
图3 个体编码结构

Step3:选择算子。本文采用轮盘赌选择，在元胞邻居结构中选择一个个体作为父代个体。

Step4:交叉算子。本文引入一种新的算子，该算子有一个很大的优势就是当父代两个个体相同时，依然能够产生新的个体，这样能够有效的避免“早熟”现象的发生。

具体操作如下图4、图5 所示:随机的产生两个切点，其中切点之间的部分进行交换保存到下一代中，然后将p1中A2的中数字内容剔除，将余下的部分进行逆转排序，同理p2也一样，将该交叉算子命名为顺序逆转交叉算子(ORX):

(1)当随机两个不相同的个体进行交叉(图4 所示)，得到的结果如下:

图4 不同的父代个体

(2)当任意给定两个相同的个体时(图5)，仍然可以进行迭代进化，不会影响其进化过程，因为即使父代两个个体相同时依旧能够获得新的子代个体，这样就能够跳出进入局部最优解，避免出现“早熟”现象。得到的结果如图5 所示。

图5 相同的父代个体

Step5:变异算子。采用逆转算子进行变异操作。其具体操作如图6 所示。

图6 逆转算子示意图

Step6:排挤技术。设置排挤因子，采用小生境技术对种群重新进行排序选择。

3.2 实例分析

选取文献［12］所描述的基于有时间窗的仓库配送问题为研究对象，该配送问题要求从1 中心仓库向8 个客户送货，中心仓库有3 辆车，每车的载重量为8 t，车辆的平均行驶速度为50km/h，且车辆的行驶时间和距离成正比，各客户的任务及要求如表2 所示，中心仓库与客户间的距离见表3。

表2 各客户的任务及要求

表3 中心仓库与各客户间的距离

为了对比算法的性能，除CNGA 之外，本文还选用了经典元胞遗传算法［10］和小生境遗传算法［9］两种算法同时对VRPTW 模型进行优化，三种算法参数设置如下:种群规模为100，交叉概率pc= 0.8，变异概率pm= 0.05，惩罚系数d = f = 50km，排挤因子为3，终止代数Generation = 100 对三种算法独立运行15 次，所得的优化结果如表4。

表4 求解的结果

为了观察逆序交叉算子的性能，在相同的算法环境以及参数条件下，分别采用新的交叉算子(ORX)、循环交叉算子(CX)以及顺序交叉(OX)算子构建了三种不同的算法，三种算法对模型进行计算，由表3 结果显示使用ORX 交叉算子得到的结果明显优于CX 和OX 算子，说明了ORX 交叉算子的有效性，而且得到的结果更接近最优值。其次通过表3可得，元胞小生境遗传算法获得配送距离平均为933，经典元胞遗传算法为976 和小生境遗传算法为947，说明元胞小生境遗传算法在求解精度上高于另外两种算法。由最优值次数和最大/ 最小值两个评价指标比较可得元胞小生境遗传算法更容易跳出局部最优解，而且算法更加稳定，由此说明元胞小生境遗传算法对求解有时间窗的车辆路径问题有很好的效果。

4 结论

带时间窗的车辆路径问题是一类复杂的NP 问题，为了获得更好的解决方法，本文在经典元胞遗传算法的基础之上，引入一种小生境技术，得到了元胞小生境遗传算法，并且将该算法应用于带时间窗的车辆路径问题时，提出了一种新的顺序逆转交叉算子，仿真实验证实新的交叉算子的性能优于传统算子，而且将元胞小生境遗传算法和另外两种遗传算法进行比较，实验结果显示新算法解的精度和算法稳定性上有更好的效果，说明该算法是解决物流配送路径优化问题的有效方法。

［1］SAVELSBERGH M. Local search for routing problem with time windows［J］. Annals of Operations Research，1985，16(4):285－305.

［2］Ho S C，Haugland D.A tabu search heuristic for the vehicle routing problem with time windows and split deliveries［J］.Computers＆Operations Research，2004，31 (2):1947－1964.

［3］Duhamel C，Potvin J-Y，Rousseau J-M.A tabu search heuristic for the vehicle routing problem with backhauls and time windows［J］.Transportation Science，1997，31(1):49－59.

［4］杨宇栋，朗茂祥，胡思继. 有时间窗车辆路径问题的模型及其改进模拟退火算法研究［J］. 管理工程学报，2006，20(3):104－107.

［5］李宁，邹彤，孙德宝. 带时间窗车辆路径问题的粒子群算法［J］. 系统工程理论与实践，2004(4):130－135.

［6］李全亮. 免疫算法在带时间窗的车辆路径问题中的应用［J］. 系统工程理论与实践，2006，26(10):119－124.

［7］张丽萍，柴跃廷，曹瑞. 有时间窗车辆路径问题的改进遗传算法［J］. 计算机集成制造系统——CIMS，2002，8(6):451－454.

［8］张智海，吴星玮. 带时间窗车辆路径问题的并行遗传算法［J］. 工业工程，2007，10(3):111－114.

［9］王辉，任传祥，尹唱唱，等. 基于小生境遗传算法的物流配送路径优化研究［J］. 计算机应用，2009，29(10):2862－2864.

［10］Alba Enrique，Bernab＇e Dorronsoro.Cellular Genetic Algorithms［M］，2008 Springer Science，Business Media，LLC，ISBN:978－0－387－77609－5.

［11］Bernab＇e Dorronsoro and Enrique Alba. A Simple Cellular Genetic Algorithm for Continuous Optimization ［C］，2006IEEE Congress on Evolutionary Computation Sheraton Vancouver Wall Centre Hotel Vancouver BC Canada，2000(6):16－21.

［12］林清国. 基于混合遗传算法的有时间窗车辆路径问题研究［D］. 济南:山东大学，2007.