基于自适应滑模变结构控制的多轴同步协调控制系统建模*

孙红涛，潘海鸿，陈 琳，李 俚，黄炳琼

(1.广西大学 机械工程学院，南宁 530004;2.广西制造系统与先进制造技术重点实验室，南宁530004)

0 引言

在现代运动控制与机械加工制造中，多轴同步协调运动控制系统已经广泛应用于数控机床、多自由度机器人、造纸、印刷、激光加工等领域［1-2］。但多轴同步运动控制过程中，由于各个轴系统参数不匹配、负载扰动、机械平台非线性摩擦、传动间隙等因素影响，容易产生同步误差［3-6］。因此本文针对两轴相对安装的直线型同步控制平台，建立同步协调控制系统模型，并采用自适应滑模变结构控制(ASMC)［7］与前馈控制(FFD)的复合控制，来完成各个轴位置闭环控制，再采用同步控制器(SYNC)完成同步误差控制。

1 同步协调控制算法研究

1.1 直线型同步控制平台模型

直线型同步控制平台模型采用轴Axis-1 和轴Axis-2 两轴轴心相对安装且在同一条直线上的结构，导轨共用，两轴滚珠丝杠之间非连接，每个轴主要由伺服电机、滚珠丝杠、光栅尺和工作台组成。伺服电机通过联轴器与滚珠丝杠相连，并驱动工作台运动，而工作台运动实际位置信息，则通过光栅尺检测。伺服驱动器采用速度控制模式，则两轴同步协调运动控制、各个轴位置闭环控制和各个轴运动控制器输出速度模拟电压信号D/A 转换，需通过运动控制卡完成。

轴Axis-1 和轴Axis-2 伺服电机通过输入大小相等方向相反同步运动命令驱动各自工作台，实现两工作台同向、位置同步运动控制。各单轴运动控制系统如图1 所示。

由于伺服驱动器采用速度控制模式，电流环与速度环集成于伺服驱动器内，因此工作台位置闭环控制需要在运动控制器上完成。运动控制器应具有设定点发生器模块、位置控制器模块、执行器模块、D/A 转换模块和测量系统模块。单轴运动控制系统数据信息流程为:

(1)设定点发生器模块产生给定位置信息Spg(单位:m);

(2)传感器模块检测工作台实际运动位置脉冲量Pulse1(单位:bit)，并将其送入测量系统模块，计算实际位置信息Pos1(单位:m);

(3)将定位置信息Spg 与实际位置信息Pos1送入位置控制器模块，进行工作台位置闭环控制，其输出为电机运行所需的速度信息ωc1(单位:rad/s);

(4)将ωc1送入执行器模块，计算并输出D/A 转换所需的数字信息Dig1(单位:bit);

(5)将Dig1送入D/A 转换模块，输出速度模拟电压量Vol1(单位:V);

(6)伺服驱动器获取运动控制器输出速度模拟电压量Vol1，经过A/D 转换模块，输出电机运行所需的速度信息ω1(单位:rad/s)，忽略A/D 转换精度与干扰信息影响，理想条件下ω1=ωc1;

(7)伺服驱动器通过传感器模块检测并处理电机实际运动速度信息ω1_fdb(单位:rad/s);

(8)将ω1与ω1_fdb 送入速度控制器模块，对电机速度进行闭环控制，其输出为电机运行所需的电流信息isq1(单位:A);

(9)伺服驱动器通过电流传感器模块检测并处理实际输入电机电流信息isq1_fdb(单位:A);

(10)将isq1与isq1_fdb 送入电流控制器模块，对电机电流进行闭环控制，其输出为电压信息usq1(单位:V);

(11)将usq1送入功率转换模块，产生3 路电压信号ua1、ub1和uc1(单位:V)，并输入电机产生转矩Tm1(单位:N·m)，从而带动滚珠丝杠与工作台运动。

1.2 同步协调控制算法

直线型同步控制平台，在两轴同向运动时，理想情况下轴Axis-1 与轴Axis-2 光栅尺位移传感器检测实际位置信息应大小相等方向相反。因此同步协调控制方法如图2 所示，Spg 为系统给定参考位置数据信息，输入轴Axis-1 位置信息为Spg，轴Axis-2 位置数据信息为－Spg，Pos1和Pos2为轴Axis-1 与轴Axis-2 光栅尺检测实际位置，则同步误差为:

各轴输入同步误差补偿量为:

其中:Sync_comp1与Sync_comp2为同步误差补偿量;Ksync为同步控制补偿器增益常数，其值需要根据同步控制系统来确定;C1与C2为同步误差补偿常数，当轴Axis-1 正向运动时，C1=C2=0.5，当轴Axis-1 反向运动时C1=C2=－0.5。

2 自适应滑模变结构控制原理

在实际工况下，运动控制系统受非线性摩擦、转矩波动等干扰因素影响，采用PID 控制并不能达到理想控制效果，因此加入具有快速响应，对外部干扰和参数变化鲁棒性能好的滑模变结构控制。

根据图1，针对轴Axis-1 定义伺服驱动器、电机和工作台集成模块传递函数表达式:

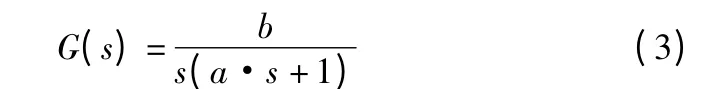
其输入为电机角速度，输出为工作台实际位置。

令状态变量x1(t)=Pos1，x2=x'1(t)，则:

其中u 为位置闭环控制输出。

系统状态方程为:

输出方程为:

令r=Spg，则输入运动控制器偏差e1为:

取切换函数S 为:

其中c 为切换函数常数。

趋近律slaw 为:

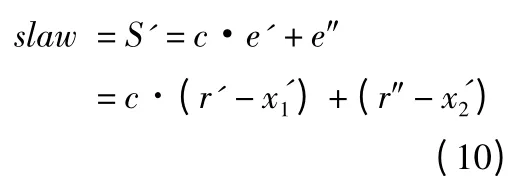
根据式(5)有

将式(11)代入式(10)得到滑模变结构位置控制器输出u 与输入关系:

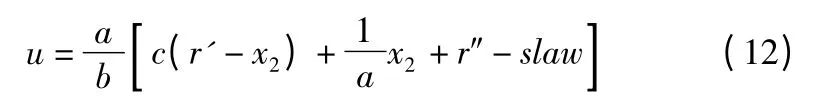
当采用指数趋近律时:

其中sgn(S)为切换函数S 符号;ε 为指数趋近律常数ε ＞0;k 为指数趋近律常数，k ＞0。

取趋近律常数ε:

由公式(14)可知趋近律参数ε 随着切换函数S自适应调整，即为自适应滑模变结构控制。

采用ASMC+FFD 复合控制后，数学表达式为:其中KV为前馈控制常数。

3 同步协调控制系统建模

根据图2 同步协调控制，采用Matlab7.0 中Simulink 工具，建立直线型同步协调控制系统模型如图3 所示。

图3 直线型同步协调控制系统Simulink 建模

为保证两轴同向同步运动，加入同步控制器。其输入为各轴位置设定点信息和反馈信息，输出为各轴运动控制器所需的同步协调控制补偿信息。同步控制器根据图2 和公式(1)与公式(2)进行建模，如图4 所示。

图4 同步控制器Simulink 建模

由于同步控制器输入为位置同步误差，而输出给各轴同步协调控制补偿量为速度信息，因此需要加入同步控制补偿器如图5 所示，其中Ksync为同步控制补偿器增益常数。

图5 同步控制补偿器

运动控制器模块用于完成轴闭环控制，输入为轴位置设定点信息、位置反馈信息和用于轴协调控制补偿信息，输出为速度电压模拟量。其内部模块如图6 所示，主要由位置控制器、执行系统和D/A 转换模块组成。

(1)位置控制器完成轴位置闭环控制，其输入为轴位置设定点信息、位置反馈信息和轴协调控制补偿信息，控制器输出为电机运动所需的角速度信息。当采用ASMC+FFD 位置控制器时，其内部模块如图7 所示，当采用PID +FFD 位置控制器时，其内部模块如图8 所示。

(2)执行系统用于将速度信息转换为数字信息，输入为电机运动所需的角速度信息，输出为数字信息，内部模型如图9 所示。其中D/A 转换采用12 位分辨率，电压范围为±10V，D/A 转换如公式(16)所示，伺

服驱动器输入电压与转速关系为0.01V/3000rpm，即10V 电压值对应3000rpm。因此转换因子K1=60/(2

其中Vout为模拟电压输出;Vref_l为参考低电平，取Vref_l=－10V;Vref_h为参考高电平，取Vref_h= +10V;N为D/A 转换所需输入的数字量。

(3)D/A 转换模块用于将数字信息转换为模拟量，输入为数字信息，输出为速度电压模拟量。其内部模型如图10 所示。

图6 运动控制器Simulink 建模

图7 ASMC+FFD 位置控制器

图8 PID+FFD 位置控制器

图9 执行系统

伺服驱动器、电机与工作台集成模块，其输入为电压模拟信号和干扰信号，输出为轴工作台实际位置信息。内部模型如图11 所示，主要由A/D 转换模块、速度处理模块和系统传递函数组成。

图10 D/A 转换模块

(1)A/D 转换模块用于将模拟信号转换为数字信息，输入为速度电压模拟量，输出为数字量。其内部模型如图12 所示。

图11 伺服驱动器、电机与平台集成模块

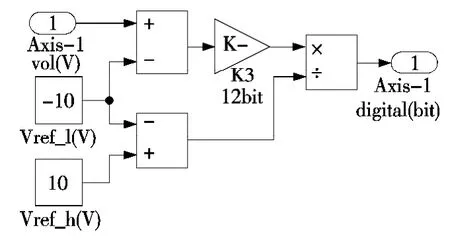
图12 A/D 转换模块

(2)速度处理模块用于将数字信息转换为速度信息，作用与轴运动控制器中执行系统模块相似，其输入为A/D 转换数字信息，输出为电机速度信息。内部模型如图13 所示，其中K4=3000/10，K5=2π/60。

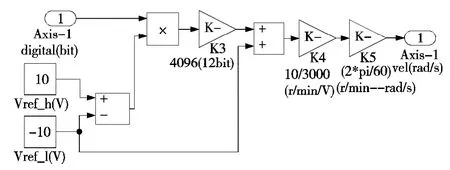
图13 速度处理模块

(3)轴Axis-1 与轴Axis-2 伺服驱动器、电机与工作台集成模块系统传递函数分别为:

4 仿真与结果分析

根据图3，为实现两轴同向同步运动控制，各轴输入位置设定点信息应大小相等，方向相反，因此仿真环境中设置为固定步长，采样周期为0.01s，仿真时间20s。输入Axis-1 位置设定点信息为Ramp 信号，斜率0.02，各控制器参数如表1 所示。采用ASMC+FFD、PID +FFD 与SYNC 不同组合，建立直线型同步协调控制系统，仿真实验结果如图14 和表2 所示。

表1 控制器参数

表2 中，Mean 为同步误差均值;SD 为同步误差标准差;RMS 为同步误差均方根;AIAE 为绝对同步误差积分均值;|max|为绝对同步误差最大值。

图14 直线型同步协调控制系统仿真结果

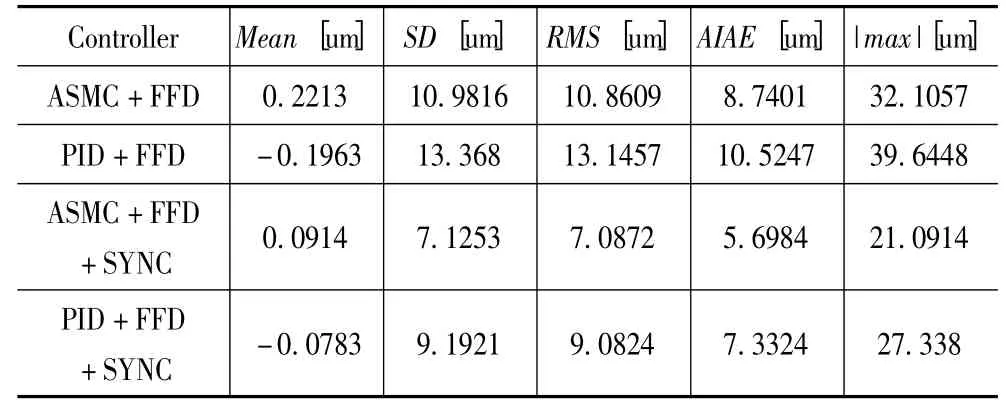
表2 直线型同步协调控制系统仿真结果

从图14 可知:图14b 和dASMC + FFD + SYNC同步误差范围约为－20 ～20um，PID + FFD + SYNC同步误差范围约为－30 ～30um，ASMC +FFD 同步误差范围约为－35 ～35um，PID+FFD 同步误差范围约为－40 ～40um。因此采用ASMC+FFD+SYNC 对同步误差范围控制效果最好。

表2 中各种控制方法组合仿真结果可知:ASMC+FFD+ SYNC 与ASMC + FFD 相比同步误差RMS和AIAE 分别降低34.75%和34.80%;PID +FFD +SYNC 与PID +FFD 相比同步误差RMS 和AIAE 分别降低30.91% 和30.33%;PID + FFD 同步误差RMS 和AIAE 分别为ASMC+FFD 的1.21 倍和1.20倍;PID+FFD +SYNC 同步误差RMS 和AIAE 分别为ASMC+FFD+SYNC 的1.28 倍和1.29 倍。因此无论采用PID + FFD 位置控制器还是ASMC + FFD位置控制器，加入同步控制器后，均能减小同步误差，而无论有无同步控制器，采用ASMC 同步误差RMS 和AIAE 均比PID 控制方法要小。

5 结束语

针对直线型双轴同步控制平台，进行同步协调控制算法与自适应滑模变结构控制算法研究。采用Matlab 完成该同步协调控制系统建模和仿真实验。实验结果表明，该直线型双轴同步控制平台加入同步控制器后，可以降低多轴同步运动过程中所产生的同步误差(RMS 值)30%左右，并且在该平台上再加入自适应滑模变结构控制与前馈控制复合位置控制器能更好地控制同步误差。以上所做的理论仿真研究为多轴同步协调控制提供一定的理论价值，表明自适应滑模变结构控制(ASMC)在多轴同步协调控制中具有较好的应用前景。

［1］Y Koren. Cross-coupled biaxial computer for manufacturing systems［J］. ASME Journal of Dynamic Systems Measurement and Control，1980，102(4):265－272.

［2］Y Koren，Ch Ch Lo. Variable gain cross coupling controller forcontouring ［J］. CIRP Proc Manufacturing Systems，1991，40(1):371－374.

［3］ R Lorenz，P Schmidt. Synchronized Motion Control for Process Automation ［C］. Proc. of the IEE-IAS Annuat Meeting，1989(2):1693－1698.

［4］J P Francisco，N Ciro，A Ricardo. Comparison of Multi-motor Synchronization Techniques［C］. Institute of Electrical and Electronics Engineers Computer Society，The 30th Annual Conference of the IEEE industrial Electronics Society，Busan，Korea，2004(12):2－6.

［5］S K Jeong，S S You. Precise Position Synchronous Control of Multi-axis Servo System［J］. Mechatronics，2008，18(3):129－140.

［6］J Ren，C W Li，D Z Zhao. CAN-based Synchronized Motion Control for Induction Motors ［J］. international journal of automation and computing. 2009，6(1):55－61.

［7］R J Wai. Adaptive Sliding-mode Control for Induction Servomotor Drive［J］. Electric Power Application IEE Proceedings，2000，147(6):553－562.