基于BP 神经网络的电主轴热误差补偿模型*

苏宇锋，袁文信，刘德平，刘武发，段智勇

(郑州大学a.机电一体化研究所;b.物理工程学院，郑州 450001)

0 引言

在高速加工中，由于高速电主轴的刚度及其精度都较高，机床加工过程中所引起的机械误差的比重较小;而电主轴的发热却不可避免，由于其发热所引起的误差已经占到了总加工误差的60%——80%，因此，对于高速主轴单元来说，采用必要的措施以较少其热误差对于机床的加工精度的影响就显得尤为重要。目前主要采用的有硬补偿和软补偿两种方法［1-3］，使用硬补偿技术的成本太高，且精度的提高有限，因此使用软补偿技术已经成为目前以及未来的主要发展趋势。本文在参考大量文献的基础上［4-9］，建立了基于BP 神经网络的电主轴热误差补偿模型，利用工具软件MATLAB 对其进行一系列仿真实验，并测试了该模型的一些精度指标。

1 电主轴BP 神经建模节点选取

在进行BP 神经网络的建模前，首先要进行必要的前期准备工作。首先利用有限元软件ABAQUS 对CX8075 加工中心电主轴进行了热-结构的耦合分析，可以得到电主轴各个节点的温升以及电主轴轴端的热变形误差的数据，这里总共分析得到了电主轴在冷却液流量为20.52L/min 和16.52L/min 两种情况下的主轴温升和热变形误差数据，其中第一组数据用于BP 网络的训练以测试其拟合的性能，第二组为测试组数据，用于对网络的预测能力的测试。分析所得到的节点的温升变化数据并不能够全部应用于建模，还需进行一系列的筛选和优化以选出电主轴的热关键点。热关键点选择的范围为电主轴的表面的46 个节点，通过在MATLAB 中进行模糊聚类的分析，最终选取了5 个与电主轴热误差线性关联度最大的节点来应用于BP 神经网络的建模，这5 个节点分别位于前法兰盘上的608 和603 号节点、后轴承架上的222 和15号节点以及主轴外壳上的218 号节点，按顺序依次编号为1 ～5，则具体的位置分布如图1 所示［10］。

图1 电主轴温度测点分布示意图

2 BP 神经网络的基本结构

BP 神经网络具有三层或者三层以上的结构，第一层为输入层，最后一层为输出层，中间的一层或者数层被称为隐含层。BP 神经网络具有信号前向传递，而误差反向传播的特点。

图2 中，Xi(i = 1，2，…，n)是神经网络的输入值;而Yj(j = 1，2，…，m)为BP 神经网络的预测值;ωij和ωjk为BP 神经网络的网络权值，它们的值会随着网络训练的过程不断更新。

BP 神经网络的结构示意图如图2 所示。

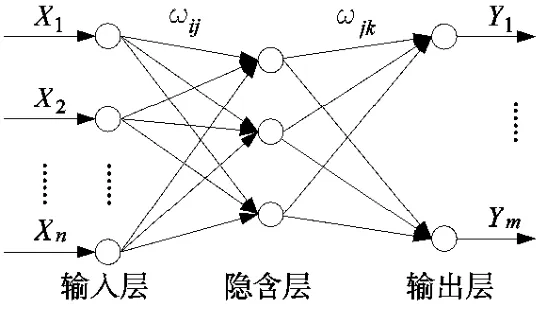
图2 BP 神经网络拓扑结构图

3 电主轴神经网络模型的训练

BP 神经网络的训练的过程即为建模的过程，只有经过训练后的网络才具备联想记忆和预测的能力。网络的训练过程包括以下几个步骤:

(1)网络的初始化:初始化输入层与隐含层、隐含层与输出层神经元之间的连接权值ωij和ωjk，初始化隐含层的阈值a 和输出层的阈值b，最后给定学习的速率和神经元的激励函数

(2)隐含层输出的计算:隐含层的输出H 的表达式如下所示:

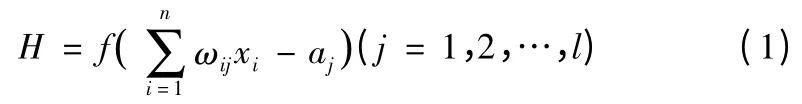
式中:l 为隐含层的节点数;f 为隐含层的激励函数。

(3)输出层的输出计算:神经网络的预测输出Ο，其计算的表达式如下所示:

(4)误差的计算:根据网络的预测输出Ο 和期望输出Y，计算网络的预测误差e。

(5)权值的更新:根据网络的预测误差e 更新网络的连接权值ωij和ωjk。

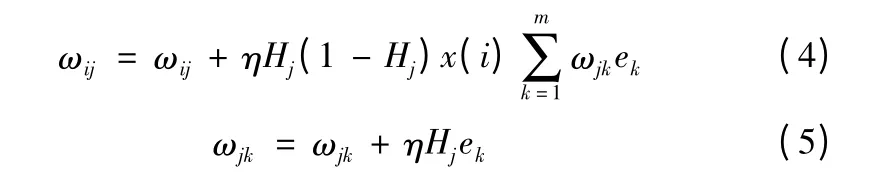
式中的η 为神经网络的学习速率。

(6)阈值的更新:根据网络预测误差e 可以更新网络的节点阈值a 和b。

(7)判断算法迭代是否结束，如果没有结束，则返回步骤2。

网络的训练在MATLAB 工具箱中来完成，在实际训练之前首先要确定网络的结构形式和一些训练参数的设定。

(1)网络的层数选择三层BP 神经网络，对于任意n 维输入到m 维输出数据的映射，它都能够胜任;输入层节点数选择选择5 个节点，分别对应之前确定的5 个温度输入变量;输出层节点数目为2，分别对应电主轴的轴向和径向的热变形误差;隐含层节点的数目确定起来比较困难，它的数目的多少将直接影响到所训练网络的质量，这里参考公式(8)和公式(9)先确定一个初始值，然后调整该值的大小，并进行多次的训练实验比较每一次的训练效果后，最终确定了选择12 个节点时效果最佳。

式中:n 为输入层神经元个数;m 为输出层的神经元个数;a 为［1，10］之间的常数。

这样最终的网络结构形式就确定为5-12-2。

(2)接下来选择网络的激励函数，第一层激励函数选择正切S 型传递函数'tansig';输出层激励函数采用了线性传递函数'purelin';网络的训练采用了系统默认的方法'trainlm'，使用该方法训练速度快，且能达到较高的训练精度。

(3)网络的最大训练次数选择1000 次，如果网络训练超过了设定次数还没有达到收敛，则要适当地增加次数;期望的误差平方和设定为0.001，虽然较小的误差值会使模型的拟合效果更好，但也同时会降低模型的预报能力;训练步长设定为初始值0.01。

需要注意的是，在进行网络的训练之前要对网络的输入和输出数据进行归一化处理，归一化后的数据再进行训练能够加快网络的训练速度，也更容易收敛，归一化的方法有很多种，这里我们采用如下的公式进行数据的归一化:

运用此公式归一化后所有的数据都限定在了区间［－1，1］中。

以下是利用MATLAB 神经网络的工具箱来完成该网络的训练和预报输出主体代码。

4 网络的拟合和预测结果

网络的训练完成之后，将第一组数据(冷却液流量为20.52L/min)中的温度变化数据再次代入训练好的网络模型中，并与误差原始值(有限元计算值)进行对比后，可以得到电主轴热变形误差的拟合对比结果，如图3 和图4 所示。

图3 径向热误差拟合对比效果图

图4 轴向热误差拟合对比效果图

将第二组数据(冷却液流量为16.52L/min)中的温度变化数据导入训练好的网络模型中，并与原始值(有限元计算值)进行对比显示，可以得到图5和图6 电主轴热误差BP 网络预报结果对比图。

由图3 ～6 中可以直观地看到，电主轴的原始热误差值与模型计算的输出结果的值非常接近，这代表运用该BP 神经网络模型能够补偿大部分的热变形误差，而运用该网络进行补偿后的误差如图中所示的残余误差曲线。

图5 径向热误差预报对比效果图

图6 轴向热误差预报效果图

另外，我们对此次训练的模型的主要精度指标进行实际的测试后，得到的结果如表1 所示。

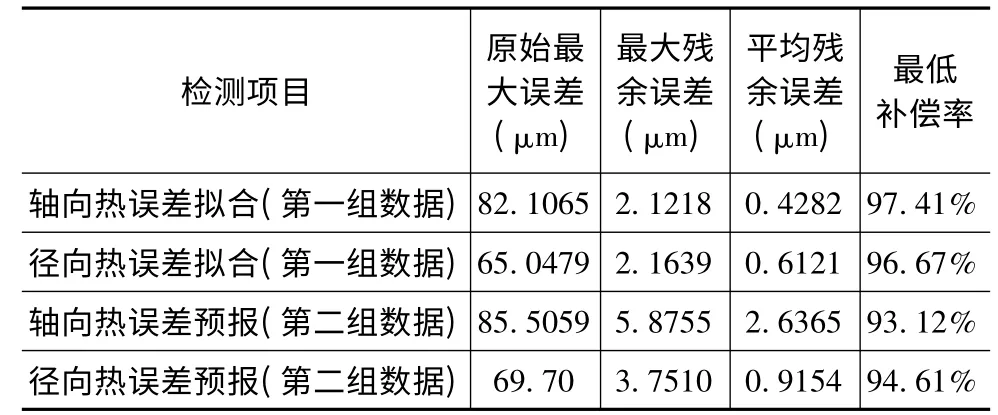
表1 BP 神经网络模型的主要精度指标

5 结束语

综上所述，利用BP 神经网络来建立电主轴的热误差补偿模型是一种可行性较高的方法，通过图2 ～5 的对比效果和表1 所测得的精度指标显示，运用该模型能够显著提高电主轴的精度，减小加工误差。然而，在实验中也发现了BP 神经网络的诸多不足之处，主要是操作者的水平要求较高，网络训练的参数比如隐含层节点数、期望误差平方和指标等等的选定需要经过多次的实验比较后才能最终确定，因此网络的训练时间较长。

［1］杨建国，张宏韬，童恒超，等. 数控机床热误差实时补偿应用［J］. 上海交通大学学报，2005，39(9):1389－1392.

［2］Jie Zhu，Jun Ni，Albert J.Robust thermal error modeling and compensation for CNC machine tools［D］，Doctoral dissertation in the University of Michigan，2008.

［3］Yang，Hong，Ni，Jun. Dynamic modeling for machine tool thermal error compensation，J. Manuf. Sci. Eng.，2003，125(2):245－254.

［4］刘永吉，沈超，化春雷. 五轴联动机床的主轴热误差补偿［J］. 机械制造，2011(6):9－10.

［5］陈莉，贾育秦，毕有明，等. 基于BP 神经网络数控机床热误差建模的研究［J］. 机电工程技术，2011，40(1):16－57.

［6］伍良生，翟少剑，周大帅，等. 基于RBF 神经网络的主轴热变形实时测量与研究［J］. 制造技术与机床，2011(8):27－30.

［7］雷春丽，芮执元，刘军. 数控机床电主轴热误差的预测方法［J］. 兰州理工大学学报，2012，38(1):28－31.

［8］文怀兴，王美妍. 高速电主轴热态性能的有限元分析及温升控制［J］. 组合机床与自动化加工技术，2010(9):52－55.

［9］李金华，刘永贤，韩家亮，等. 车削中心主轴系统热特性有限元分析的研究［J］. 组合机床与自动化加工技术，2011(11):6－8，11.

［10］苏宇锋，袁文信，刘德平，等. 高速电主轴热——结构特性研究［J］. 组合机床与自动化加工技术，2012(1):25－27.