多目标驱动的立式精密磨床床身优化设计方法研究*

许春雷，郑清春，杨常青，胡亚辉

(天津理工大学 复杂系统控制理论及应用重点实验室，天津 300384)

0 引言

床身是数控机床的重要支撑部件，提高其结构特性对整机的加工精度、抗振性有重要意义。传统设计主要通过经验法和类比法进行，造成结构较为笨重。许多学者运用有限元方法进行了深入的研究［1-3］。本文基于多目标优化方法，利用ABAQUS 仿真研究如何在保证床身刚度和固有频率的前提下对床身进行轻量化设计，对提高机床制造的经济性有重要意义。

1 磨床床身的有限元分析

本文研究对象取自于天津某机床厂1.25 立式精密磨床，该型数控精密立式磨床由床身、立柱、工作台和滑板等组成，如图1 所示。在保证刚度的前提下对其进行轻量化优化设计，就要对这些部件进行强度、刚度及抗振性分析。本文对床身进行静动态分析并提出改进方案。用ABAQUS 有限元分析软件对床身进行有限元分析，首先在Solidworks 三维制图软件中建模，然后将模型导入ABAQUS 软件中进行分析并读取静态分析和模态分析的结果。

1.1 床身力学性能分析

床身所用材料为灰铸铁HT300，弹性模量E =143GPa;泊松比μ=0.27;密度ρ =7.25 g/cm3;强度极限σb≥300MPa。

床身受力如图1 所示。经Solidworks 质量计算可以计算得出立柱及其以上部件总重力:

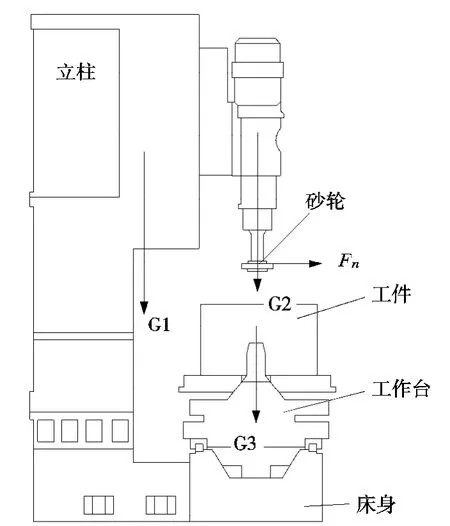
图1 机床结构及受力简图

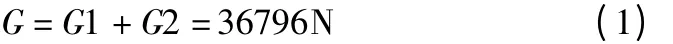
由切削力的切向力公式:

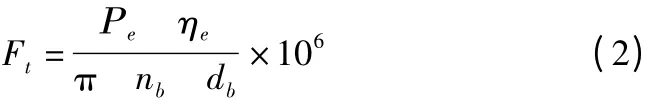
上式中Pe为电机功率16kW，ηe为电机的传动效率0.9，nb为砂轮的转速40.6r/s，db为砂轮的直径300mm，计算出切向力Ft=375.6N。由于法向的切削力Fn是切向力的2.4 倍，所以Fn=901.4N。最后得出立柱对床身结合面处产生压力P =0.113MPa，扭矩为M=9.7838N·mm。同理分析得出床身导轨处压力P=0.696MPa。

1.2 床身有限元模型建立

磨床床身属于结构铸件，有许多铸造圆角、工艺孔、拔模角、螺纹孔和装配定位结构。这些结构对床身的力学性能影响很小但在有限元分析中会占用很大的资源，所以在建立有限元模型时有必要对其结构进行简化。简化的原则是确保结构力学性能受到的影响最小。

图2 床身有限元模型

图2 所示床身底部与地基接触面添加位移全约束实现对床身的固定。在导轨平面划分出滑块的接触面，施加载荷压力0.696MPa。床身与立柱结合面处施加压力0.113MPa，并使用耦合功能施加扭矩9783800 N·mm。

对床身进行静态分析和模态分析得到其静态力学性能和固有频率，要定义一个通用静力分析步以输出最大应力和最大变形，还要定义一个静态线性扰动分析步输出床身前10 阶固有频率。

1.3 查看有限元分析结果

将有限元模型提交求解器选用standard 模块。计算结束后在后处理模块查看输出的结果。

(1)静态分析结果

在后处理模块中选择输出通用静力分析步的结果，可以看到床身最大变形发生在床身与立柱接触面的边缘。最大变形量为1.724μm，最大应力为1.191MPa。结果如图3 所示。

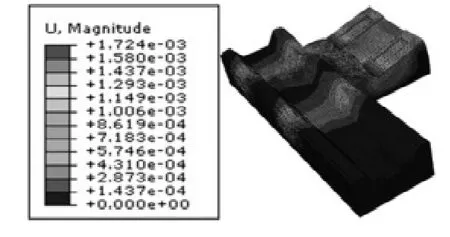
图3 床身位移云图

(2)模态分析结果

在后处理模块中选择输出静态线性扰动分析步结果。

表1 床身各阶固有频率

从表1 结果可以看出床身的各阶固有频率都远远大于激振频率，所以在优化床身的过程中只把床身的固有频率作为验证条件。

2 床身结构优化

床身可以从几何形状、拓扑结构、结构尺寸来调整。由于改变床身结构的几何形状会造成生产工艺上的巨大改变，成本太高所以这里不作调整。从有限元分析结果发现床身外壁的变形比较小而床身外壁厚度较大且壁厚也不同，给加工和快速设计带来不便，从快速设计和标准化出发把承重壁厚定为60mm。支撑立柱最内侧的筋板变形较大，将其厚度从20mm 增加到40mm。其他结构保持不变。在Solidworks 中建出新型床身的简化模型并导入ABAQUS 中进行分析并查看结果。

表2 两型床身对比表

通过表2 对比，床身结构改变后床身最大变形量增大很小而重量减轻很多，所以新型结构是可用的。

3 基于灵敏度分析的参数优选

床身在一定的结构下力学性能由结构尺寸决定，同时结构尺寸也决定床身重量。根据厂家保证床身刚度同时降低床身重量的要求，需要对床身的结构尺寸进行优化。

床身结构尺寸中，床身的框结构尺寸(如床身的长、宽、高)由磨床的功用或按照人机工程学［4］来决定的。选取床身的壁厚、筋板厚度作为设计变量，见表3。

表3 各设计变量及其符号

选取各个设计变量如图4 所示。

图4 床身设计变量示意图

运用灵敏度分析的方法［5］，确定各个实际变量对床身重量和最大变形量的关键参数。缩减一些次要设计变量，可以明显提高结构优化设计效率。从数学意义上，灵敏度可解释为:若函数F(x)可导，其一阶灵敏度可表示为:

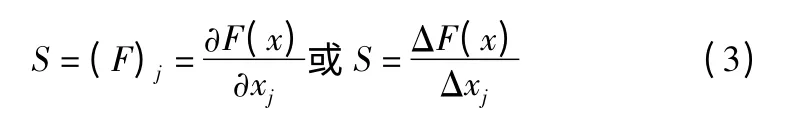
3.1 设计变量对床身重量的灵敏度分析

床身质量由其体积决定，设计变量对床身体积的影响越明显则对质量的影响也越明显。在Solidworks 中可以方便的测得床身壁厚和筋板的侧面积，然后求出其体积，结果如下:

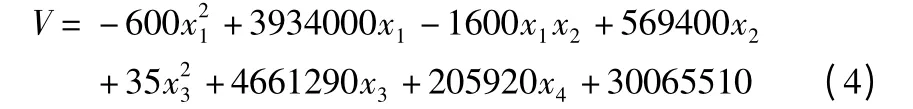
通过灵敏度分析得到设计变量对床身体积即是对床身重量的灵敏度值。

表4 各个设计变量对床身质量灵敏度值

通过表4 可以看出各个设计变量对床身重量的灵敏度X3＞X1＞X2＞X4。

3.2 各设计变量对床身最大变形量的灵敏度分析

本文通过正交试验设计，运用ABAQUS 软件获取仿真数据，通过多元线性回归得到设计变量与床身最大变形量之间的函数关系式从而分析各设计变量的灵敏度。

(1)基于Excel 和python 的模型建立

安排L25(45)正交试验，实验需要做25 次，如果建25 个模型工作会很繁琐，Solidworks 中尺寸可以通过Excel 表格进行驱动，见图5。

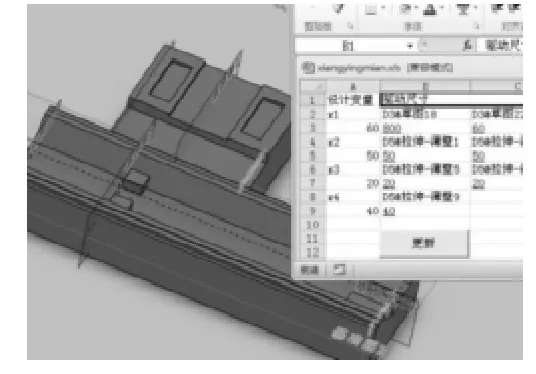
图5 Excel 驱动Solidworks

在Excel 中建立设计变量与驱动尺寸的关系，然后插入一个按钮，按钮添加宏如下:

将Excel 表格添加到Solidworks 的设计活页夹中，将设计变量值输入到Excel 中然后点击更新按钮就会生成新的模型。

将生成的模型导入ABAQUS 中进行分析，对于重复的步骤，如定义材料，定义分析步等可以通过录制宏来得到python 语言代码执行繁琐的操作。如定义材料部分的python 语言代码如下:

(2)基于ABAQUS 的仿真结果及分析

将正交试验得到实验数据最大应力S(MPa)和最大变形U(μm)整理如表5 所示。

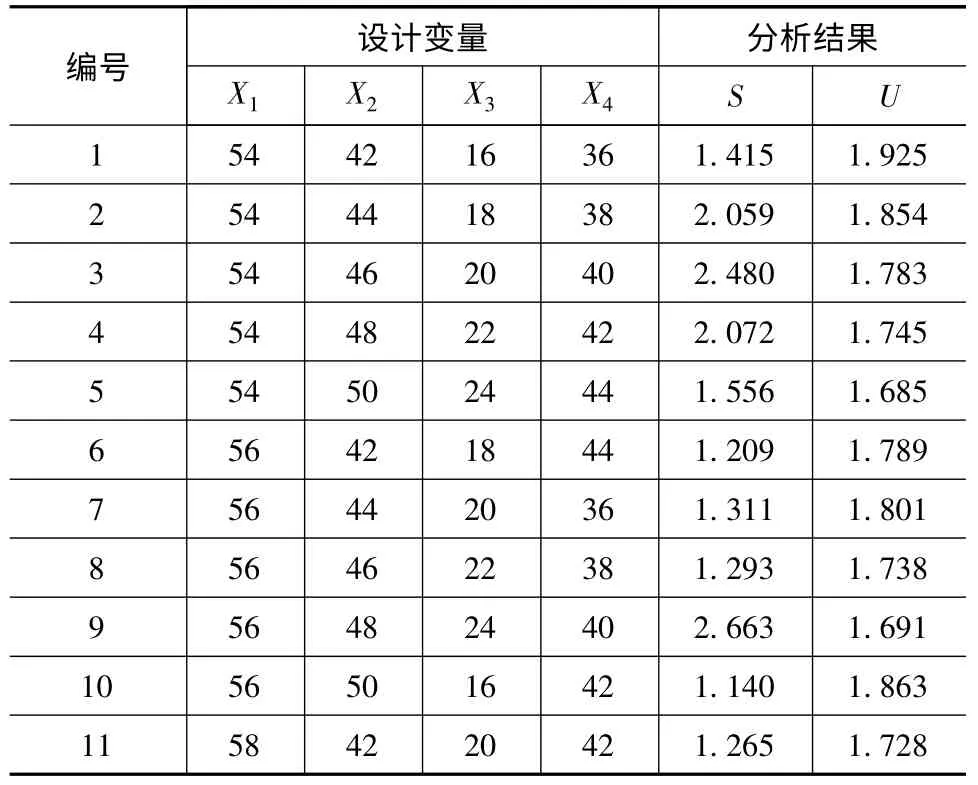
表5 正交试验结果

(续表)

对结果做线性回归分析，回归方程的形式为:

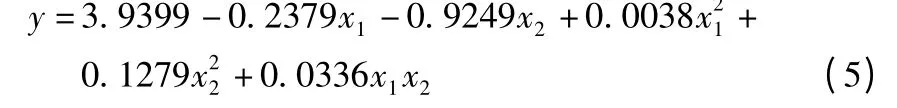
运用Matlab 多元线性回归分析函数regress 进行回归分析计算。结果方程为:

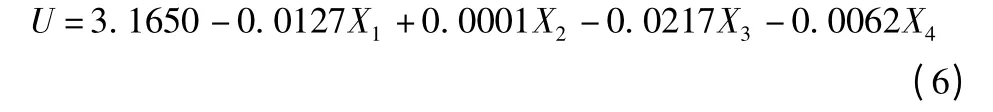
决定系数R2= 0.99，显著性检验统计量F =546.4，剩余方差P ＜0.0001。从结果中可以看到F检验的P 值接近于0，F0.05=2.8661 远远小于F =546.4;决定系数R2=0.99 接近于1，说明回归方程是有意义的。

表6 各个设计变量对床身最大变形量灵敏度值

通过表6 看出设计变量对床身最大变形量的灵敏度X1＞X3＞X4＞X2。

综合考虑各个设计变量对床身重量和最大变形量的灵敏度，选取优化参数为X1(床身承重壁厚)和X3(普通筋板厚度)。

4 床身结构参数的多目标优化

响应曲面设计方法［6］(RSM)是利用合理的试验设计方法得到数据，采用多元回归方程来拟合因素与响应值之间的函数关系，通过对回归方程的分析来寻求最优工艺参数，是解决多变量问题的一种统计方法。

4.1 实验数据的采集

采用中心复合试验设计(CCD)来安排实验。按要求选取中心点、轴向点和立方点，取变量值x1(cm)(承重壁厚度)、x2(cm)(普通筋板厚度)安排实验，读取最大变形量u(μm)和质量m(t)，得到结果如表7 所示。

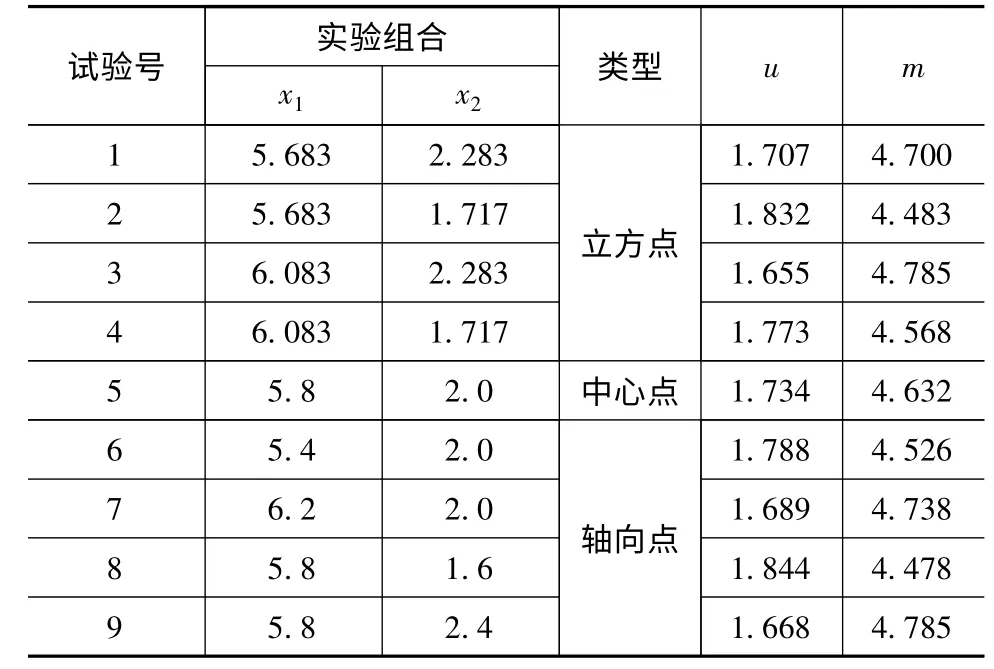
表7 中心复合试验设计结果表

4.2 拟合响应面模型函数

响应面函数最常用的是二次函数，形式如:

二次响应面模型有较高的精度能满足工程实际的需要。运用Matlab 对表7 中的数据进行二次回归分析，得到设计变量与床身重量和床身最大变形量的二次响应面模型，并进行有效性检验。

床身最大变形量的响应面模型

F 检验统计量F =971.66 远远大于F0.01 =10.92 所以模型是有效的。

床身重量的响应面模型:

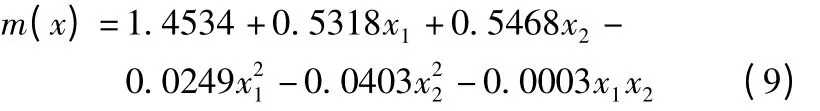
F 检验统计量F =370.15 远远大于F0.01 =10.92 所以模型是有效的。

4.3 床身多目标优化的实现

将床身重量和最大变形量同时作为优化目标进行优化，数学描述如下

采用理想点法求解多目标优化问题，首先运用Matlab 分别求取u(x)和m(x)的最优解U =1.7097和M=4.6568 即理想点，然后构造评价函数如下:

再求取评价函数f(x)最优解，得到x1=5.72 和x2=2.14。取x1=5.7cm 和x2=2.2cm 建模分析，结果如表8 所示。

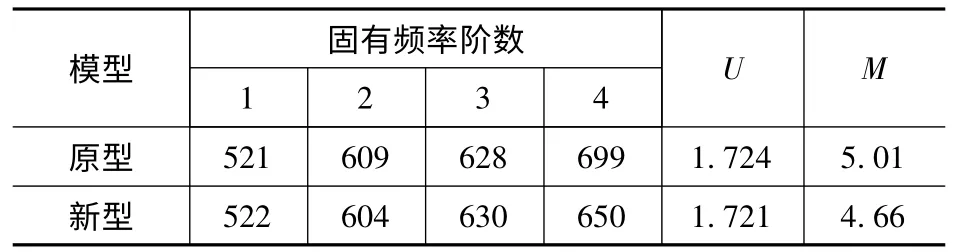
表8 优化后的床身有限元分析结果

从结果可以看出优化后的新型床身最大变形量有所减小，与原型床身对比床身重量降低了7%，达到了厂家保持最大变形量不增大而降低床身重量的要求。

5 总结

本文运用ABAQUS 有限元分析软件，对1.25 立式磨床的床身进行结构优化，通过灵敏度分析确定灵敏的设计变量，采用理想点法实现对床身重量和最大变形量响应面模型的多目标优化，经实际生产证明，符合厂家要求，在保证低成本的情况下，设计是有效合理的。说明这种方法是可行的，可以很好地指导产品结构优化，有实际应用价值，亦可推广到其他工程优化领域。

［1］钟伟弘，徐燕申，林汉元. 基于有限元分析的模具加工中心床身结构优化设计［J］. 组合机床与自动化加工技术，2009(3):21－24.

［2］陈桂平，文桂林，崔中. 高速磨床床身结构动态分析与优化［J］. 制造技术与机床，2009(2):19－23.

［3］耿新海. 六主轴数控车床床身有限元分析与结构优化［D］. 沈阳工业大学，2009.

［4］丁玉兰. 人机工程学(第3 版)［M］. 北京:北京理工大学出版社，2005.

［5］罗辉，陈蔚芳，叶华. 机床立柱灵敏度分析及多目标优化设计［J］. 机械科学与技术，2009，28(4):487－491.

［6］熊俊涛，乔志德，韩忠华. 基于响应面法的跨声速机翼气动优化设计［J］. 航空学报，2006，27(3):399－402.