一种点云数据曲线光顺处理算法*

王 可，唐忠辉，孙兴伟

(沈阳工业大学 机械工程学院，沈阳 110870)

0 引言

随着科学技术的进步，尤其是计算机辅助工程在产品开发中的广泛运用，人们对产品的性能与外观要求日益提升，而产品的光顺程度是其中的一个重要影响因素，因此，产品表面的光顺性就显得尤为重要。光顺处理也一直是CAGD 中的一个研究热点，它在汽车、船舶、航空、航天等众多领域应用越来越广泛，对它的研究具有重要的理论及应用价值［1］。从产品制造加工的角度来说，设计产品的几何光顺性不好会导致加工困难，生产效率低下，从而使加工成本提高。除此之外，曲线曲面的光顺性对产品的物理性能、产品的质量和产品的外观等都将产生重要的影响。所以，曲线曲面的光顺处理一直受到了工业界、学术界的广泛关注。

近年光顺拟合的研究较多，关于曲线的光顺处理方法，总体上可分为两类:整体光顺法和局部光顺法［2］。曲线的整体光顺方法常用的有能量法、小波法和最小二乘法［3］。基于光顺原理可分为基于节点删除、插入的光顺;其中，最早最有影响力的光顺方法是1987 年Farin［4］等提出的一种通过“节点消去与插入”的B 样条曲线光顺方法，该方法的本质是利用曲线的曲率图进行人工交互修改，以使曲率变化比较均匀，最终达到曲线光顺的要求。

在众多数据处理方法中，最小二乘法是其中一种较常用的数据拟合方法。但当处理点云数据时，如果只采用一条曲线函数拟合点云数据，当多项式阶数太低，拟合精度达不到预定效果。要提高拟合精度和效果就需要提高拟合曲线阶数，但阶数太高又带来计算上的复杂性和难操作性，甚至出现龙格现象，很难取得较好的拟合效果和精度。如果采取分段拟合，拟合后的曲线在分段处可能不连续。为了有效地解决上述问题，本文提出了基于拉格朗日乘数法点云数据光顺处理的方案。

1 数学模型的建立

在现代工业革命的进程中，为了利用先进制造技术与方法，需要通过一定处理，然后将实物模型转化为CAD 模型，最后反求出该产品的数学模型，从而将产品实物转化为产品数学模型，进一步研究出同类的先进产品的科学技术称为“逆向工程”，又称“反向工程”或者“反求工程”［5］。在将实物模型转化为CAD 模型的过程中，为了保证反求出的产品模型尽可能接近产品实物，需要得到产品实物表面上的大量的离散点，这些离散点一般称为点云数据［6］。由于原始数据庞大，因此，对数据曲线拟合往往不可以在全域上进行拟合，而是分段多次在不同数据点上进行拟合［7］。

定义:在分段曲线拟合中，进行一次曲线拟合所包括的点数区间称为窗口。

本文分段曲线拟合是在每一个窗口中进行拟合，得到一条多项式拟合方程，输出前两个数据之间的拟合曲线，然后窗口向后移动一个数据点，组成下一个拟合窗口再进行下一次的拟合，一直拟合完最后一个窗口。如下图1 是用M 个点为一个窗口去拟合N 对数据点，共有N－M +1 个窗口。

图1 分段曲线拟合示意图

设点云数据区间为［x1，xN］，设N 对型值点为(xj，yj)(j = 1，2，…，(N－1)，N)，每个窗口逼近多项式g(x):

其中:在窗口1 中是采取传统意义上的最小二乘法拟合，即可求的拟合多项式g1(x)。

设在第k 个(k = 2，3，4，…，(N－M +1))窗口的多项式为:

式中:ak0，ak1，ak2，…，ak(n－1)，akn为待定系数。

为保证曲线在xk处，gk－1(x)过渡到gk(x)时曲线连续，要求前后两段曲线在xk处的函数值相等，即要加入端点约束条件:

同时，为保证曲线在xk处，gi－1(x)过渡到gi(x)时曲线光顺，要求前后两段曲线在xk处的一阶导数值也相等，即加入端点约束条件:

2 数学模型的求解

该数学模型是一个带极值的约束问题，本文采用拉格朗日乘数法［8］，将条件极值问题转化为无条件极值问题来求解.以第k(k = 2，3，4，…，(N－M +1))个窗口为例，具体方法如下:

引入拉格朗日乘子λl(l = 1，2)，并设Hk=gk(xk)－ gk－1(xk)，Kk= g'k(xk)－ g'k－1(xk)，所以，模型的边界约束条件为:

Hk= 0， Kk= 0

则拉格朗日函数为:

其中:xk＜xj＜xk+M－1。

为了使拟合后的曲线尽可能的逼近测量值，就必须拉格朗日函数值Q 最小，可以改变系数aki值的大小，为此令Q 对每一个系数求偏导数，并令其偏导数为零，即:

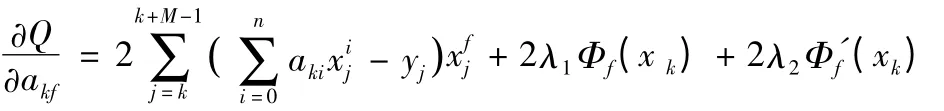
其中:Φf(x)= xf，f = (0，1，2，3，…，n)

写成矩阵的形式有:

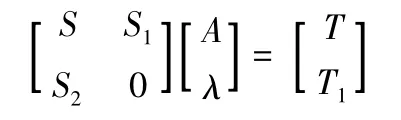
其中:

其中

由以上矩阵方程即可求出拉格朗日函数中系数aki(i = 1，2，3…n)以及λl(l = 1，2)，从而可以得到数据点［k，k +1］之间拟合曲线，根据该方法依次求解，即可得到全域上的拟合曲线。

3 应用实例

下面给出该算法在螺旋曲面测量光顺问题中的一个应用实例。工程中在加工测量螺旋曲面截面廓形的时候，一般是用千分尺测量截面的大小径，然后通过测量数据来设定数控机床的下一步刀补，该测量方法工作效率低且测出的数据精度不是很理想。本文采用激光测量连续测量螺旋曲面截面廓形上的点，由测量值组成整个截面廓形，如图2。

图2 测量值组成的截面廓形

将图2 中左上方的小方框位置进行局部放大后如图3 所示，可以看到因测量仪器的误差、加工时工件的振动以及工件表面刀花等因素的影响，测得的点云数据是一条不光顺的封闭曲线，因此，需要对测量点进行光顺处理。由于测量得到的数据是一组密集的点云数据(大径10cm 左右的螺杆外轮廓测量2000 个数据点)。用现有的方法无法有效地对其进行光顺。

图3 原螺旋曲面廓形局部放大分布图

由于测量所得螺旋曲面廓形是由测量值组成的封闭曲线，不能使用本文的光顺方法，要先将其表示成极坐标的形式，即r = r(θ)，θ ∈[ ]0 360 ，如图4 所示。

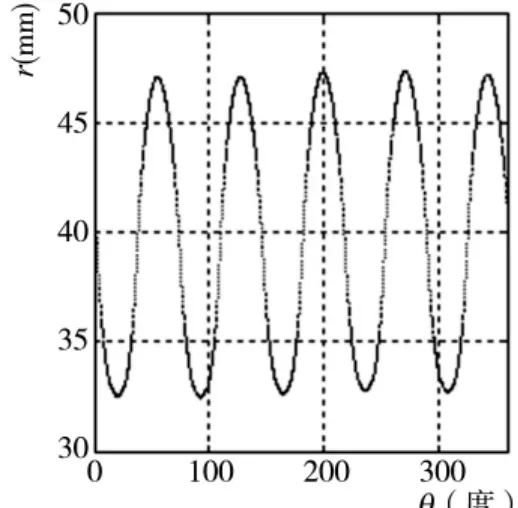
图4 极坐标下截面廓形

应用本文提出的基于拉格朗日乘数法对点云数据光顺处理的算法进行光顺。在计算机上编写相应的算法程序，经过多次试验，当选取选取五点为一个窗口，二次多项式为拟合函数时，处理后数据效果最佳。处理后得到的光顺后曲线局部放大图，如图5所示。

通过光顺后曲线与原测量值的比较可以看出，光顺后曲线连续，并且在原型值点组成的曲线局部出现了细微的波动被本文光顺算法所光顺，并且曲线的一阶导数全域上连续，使之成为连续的光顺曲线，并且光顺后的曲线在原曲线的型值点列波动的中心范围内穿过，因此拟合曲线较合理。

图5 曲线的光顺效果

选取局部放大图的50%的测量点作为计算样本进行数据分析，如表1 所示。从表1 可知:原测量值与经本文算法光顺后曲线上对应的点比较，最大偏离误差值不超过0.1mm，偏移幅度小于0.5%，因此拟合精度高。

表1 光顺前后数据

(续表)

4 结论

本文针对目前点云数据光顺算法存在的问题，提出了一种基于拉格朗日乘数法对点云数据光顺处理的算法。显示该算法能很好保持曲线原有性质的基础上使曲线连续及一阶导数全局连续，证明了处理后的曲线光顺效果较好，同时避免了使用高次曲线拟合带来的种种弊端。达到了对点云数据预期的光顺效果。为逆向工程中的点云数据中曲线光顺处理提供一种有效的数学算法。

［1］李道军，许春香. 拟合曲线光顺方法的研究［J］. 信息技术，2011:277－278.

［2］章虎冬. 参数三次样条曲线的局部优化光顺算法［J］.西安邮电学院学报，2011，16(2):68－70.

［3］赵罡，王爱增，穆国旺. 基于小波的非均匀B 样条曲线自动光顺算法［J］. 计算机辅助设计与图形学学报，2010，22(11):1925－1931.

［4］Farin G，Hoschek J，Kin M S. Handbook of Computer Aided Geometric Design［M］. Amsterdam:North Holland，2002:121－125.

［5］赵宇明，张国忠，于哲峰. CATIA 软件在汽车逆向设计点云处理技术中的应用研究［J］. 机械设计与制造，2005(6):80－82.

［6］刘丹. 基于点云数据的曲线拟合［D］. 辽宁:辽宁工程技术大学，2009.

［7］张旭臣，卢全海. 基于分段二次样条函数的水位流量关系曲线拟合方法研究［J］. 水文，2010，30(4):59－62.

［8］同济大学应用数学系. 高等数学(下册)第五版［M］. 北京:高等教育出版社，2006.