模糊PID 在CNC 粉末液压机控制系统中的应用研究*

吴士鹏，徐 蕾，俞建卫，2

(1.合肥工业大学 摩擦学研究所，合肥 230009;2. 安徽省粉末冶金工程技术研究中心，合肥230009)

0 引言

粉末冶金数控液压机电液伺服系统的控制性能直接影响粉末冶金产品的品质，这主要表现在两个方面:首先，位置控制直接影响粉末冶金产品的几何形状和尺寸精度，因此实时位置控制是粉末冶金液压机的主控参数;其次，为了保证粉末产品的密度均匀性以及防止粉末在压制过程中的横移，各模冲的压制速率必须相等，因此对模冲的速度控制要求很高。由于粉末冶金液压机电液伺服控制系统在工作过程中受到如油液黏度、温度、现场工况等多种参量因素的影响，表现出时变、干扰等不确定性，而常规的PID 算法，对于时变性、强干扰系统的控制自适应能力差，难以达到理想的控制效果。为解决这一问题，可以通过实时调整PID 参数来实现。

模糊控制已成为智能自动化控制研究中最为活跃而又富有成果的领域［1］。其中，模糊PID 控制扮演了非常重要的角色，并将成为未来控制理论研究与应用的重点技术之一。到目前为止，虽然PID 控制在工业过程控制应用中仍占有主导地位，但是在一些具有参数时变性、强干扰、不确定的工业控制系统中，PID 控制表现出明显的缺陷，如不能够进行自适应控制、控制过程中超调量过大或者控制严重振荡甚至失控。而模糊PID 控制器可以满足不同工况对PID 参数自整定的要求，特别适合对具有时变性、强干扰、不确定系统的控制。因此，本文将模糊PID控制应用到CNC 粉末液压机电液伺服控制系统以提高其控制性能。

1 CNC 粉末液压机的位置与速度控制模型的建立

如图1 所示，CNC 粉末液压机电液伺服控制系统主要由控制器、电液伺服阀、液压缸、位移传感器组成。为了建立CNC 粉末液压机控制系统的数学模型，必须对CNC 粉末液压机电液伺服控制系统的主要组成元件进行分析。

图1 CNC 粉末液压机电液控制系统

1.1 电液伺服阀的传递函数

电液伺服阀是电液伺服系统的核心元件，是连接电气元件与液压元件的纽带。其性能对整个系统特性有很大影响。由于在大多数电液伺服控制系统中，伺服阀的动态响应往往高于执行元件的动态响应。因此，为了简化系统的分析，伺服阀的传递函数一般可以用二阶振荡环节来表示。故设伺服阀的传递函数为:

式中，ksv—伺服阀的流量增益;ωsv—伺服阀的频率;ξsv—伺服阀的阻尼比。

1.2 伺服液压缸的传递函数

伺服液压缸作为电液伺服系统的动力执行元件，与普通液压缸相比，可以实现对位置、速度的精确控制。在建立液压缸的模型时，需要阀的线性化流量方程、液压缸的流量连续方程以及液压缸与负载的平衡方程这三个方程，具体的建模过程可参见文献［2-3］，这里不再赘述，只给出液压缸活塞位移与阀芯位移之间的传递函数模型，如式(2)所示。

式中，Xv—伺服阀的阀芯位移;Xp—液压缸活塞位移;Ah—液压缸活塞杆的面积;ξh—液压缸的阻尼比;ωh—液压缸的响应频率。

1.3 CNC 粉末液压机的位置与速度控制模型

根据CNC 粉末液压机的工作要求，分别选用力士乐4WS2EM6-2X 型伺服阀以及力士乐CG280D630 型伺服液压缸作为CNC 粉末液压机电液伺服系统的伺服阀与伺服缸。通过查阅伺服阀与伺服缸的使用手册，最终确定液压控制系统各参数，如表1 所示。

将式(1)、式(2)的伺服阀与伺服缸的传递函数联立相乘，并将表1 的参数值代入，则可得CNC 粉末液压机的位置控制系统的开环传递函数为

对式(3)进行积分，则可得到速度控制系统的开环传递函数为

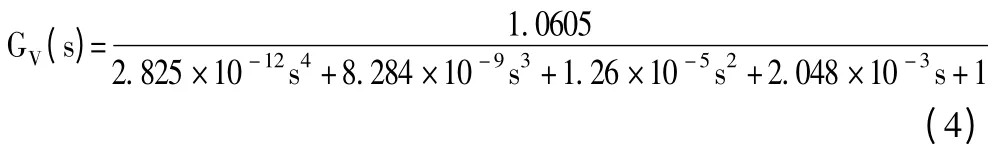
表1 液压系统参数值

2 CNC 粉末液压机的模糊PID 控制器设计

2.1 模糊PID 控制器的基本原理

模糊PID 控制器由PID 控制器和模糊控制器两部分构成，其结构如图2 所示。模糊自整定PID 设计思想是先找出PID 三个参数与偏差e 和偏差变化率ec 之间的模糊关系，在工作中通过不断检测e 和ec，再根据模糊控制原理对PID 的三个参数进行在线校正，以满足不同e 和ec 对控制器参数的不同要求，而使被控对象有良好的动、静态性能。其工作过程可大致分为这几个步骤:首先，控制器输入量的模糊化;其次，依据模糊控制规则，应用模糊逻辑推理得出控制器的模糊输出量;第三，将模糊输出量乘以量化因子得到精确量即PID 三个参数的调整量;最后，将PID 三个参数的调整量分别与PID 的初始值相加，得到PID 新的控制参数。

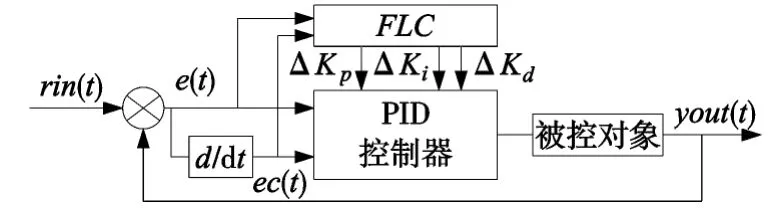
图2 模糊PID 控制器结构

模糊PID 控制器调整PID 参数计算公式［4］为:

式中，K'p、K'i、K'd—模糊PID 控制器的初始PID 参数，ΔKp、ΔKi、ΔKd—PID 参数的调整值。

2.2 确定语言变量及其隶属函数

模糊PID 控制器以系统误差e(t)、误差变化率ec(t)为输入，以PID 参数的调整量ΔKp、ΔKi、ΔKd为输出。因此，选取e(t)、ec(t)、ΔKp、ΔKi、ΔKd为模糊PID 控制器的语言变量。对于这5 个语言变量，各个语言变量的语言值选用NB(负大)、NM(负中)、NS(负小)、ZO(零)、PS(正小)、PM(正中)、PB(正大)这7 个语言值来描述。输入变量e、ec 的模糊论域均为{－3，－2，－1，0，1，2，3};输出变量ΔKp、ΔKi和ΔKd的模糊论域也均为{－3，－2，－1，0，1，2，3}。为了计算的方便，模糊PID 控制器的输入、输出变量均选用三角形和高斯曲线形的隶属函数。隶属函数的图形如图3 所示。

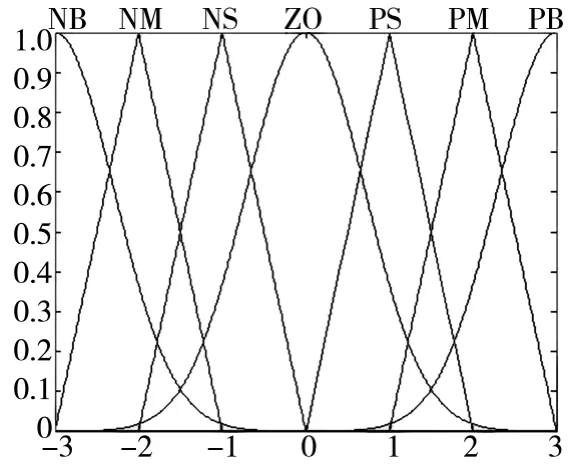
图3 模糊PID 的输入、输出变量隶属函数

2.3 模糊规则的确定

根据Kp、Ki和Kd三个参数在PID 控制过程中的作用，可以归纳出PID 的3 个参数在控制过程中的调整规则:

(1)参数Kp的作用是减小系统误差，增加系统响应的快速性。它主要与系统的偏差有关，当系统误差|e(t)|较大时，Kp也较大;而当系统误差|e(t)|较小，Kp也较小。参考文献［5］建立如表2 所示的Kp的模糊控制规则。

表2 Kp 的模糊控制规则表

(2)Ki的作用是消除系统的稳态误差。Ki越大，系统稳态误差消除越快，但是Ki过大，则系统在响应过程的初期会产生积分饱和现象，从而引起响应过程的较大超调;若Ki过小，系统的稳态误差难以消除，从而影响系统的调节精度［6］。因此，可建立如表3 所示的Ki的模糊控制规则。

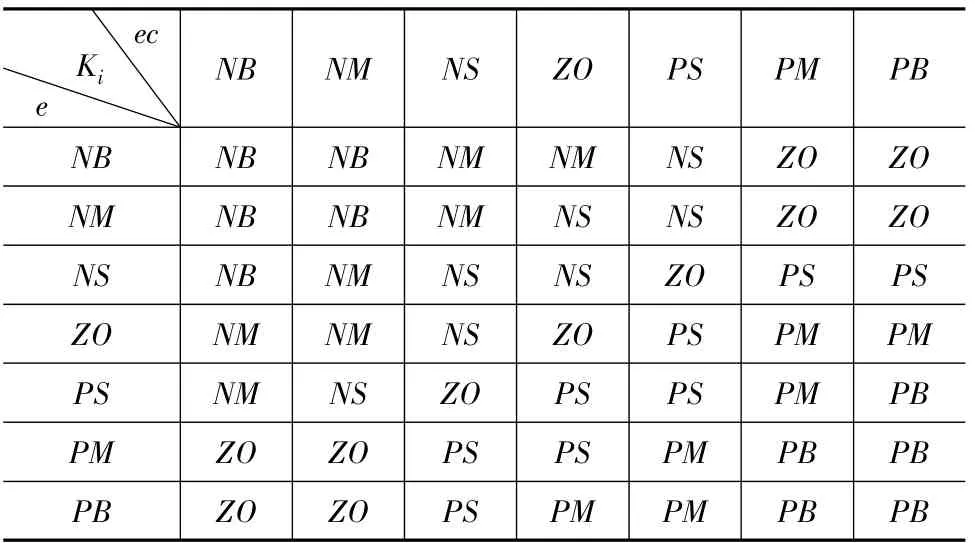
表3 Ki 的模糊控制规则表

(3)Kd的主要作用是在抑制系统误差向任何方向的变化，对误差变化进行提前预报。但Kd过大，会使响应过程过分提前制动，从而延长系统调节时间，并且系统的抗干扰能力差。参考文献［7］建立如表4 所示的Kd的模糊控制规则。

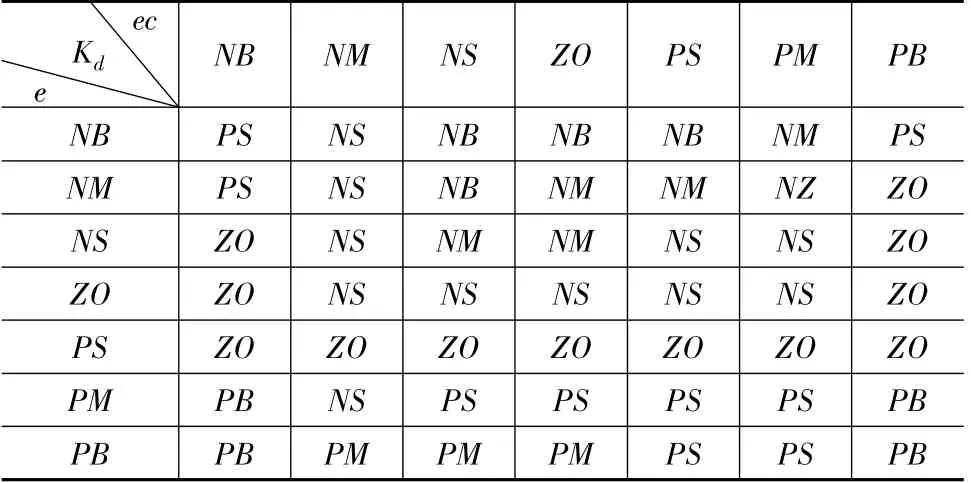
表4 Kd 的模糊控制规则表

2.4 模糊推理与模糊判决的确定

对位置与速度模糊PID 控制均采用Mamdani 推理法进行模糊推理运算，并都采用加权平均法进行模糊判决。另外，为了便于模糊PID 控制器的实时控制，采用的模糊控制算法是查表法。

3 CNC 粉末液压机电液伺服控制系统单位阶跃响应分析

为了检验所设计的位置与速度模糊PID 控制器的控制性能，在单位阶跃信号输入下，分别在系统无干扰、系统加干扰以及系统阻尼比ξh发生变化这三种状态下对PID 控制与模糊PID 控制进行仿真分析。

3.1 系统正常状态下单位阶跃响应仿真分析

根据CNC 粉末液压机位置控制系统的数学模型(式(3))与速度控制系统的数学模型(式(4))，分别对模糊PID 控制与PID 控制进行单位阶跃响应仿真实验。位置与速度控制的仿真结果分别如图4、图5 所示。

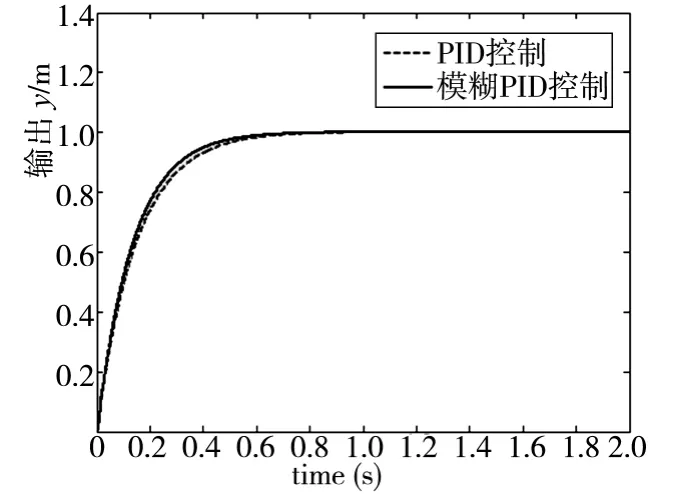
图4 位置PID 控制与模糊PID 控制的单位阶跃响应

图5 速度PID 控制与模糊PID 控制的单位阶跃响应

从图4、图5 可以看出，在单位阶跃响应的初始阶段，与PID 控制相比，位置模糊PID 控制与速度模糊PID控制的单位阶跃响应的上升时间与调整时间更短，表现出了比PID 控制更优的控制性能。为了进一步对PID 控制与模糊PID 控制的控制性能进行量化比较，分别计算出位置、速度的PID 控制与模糊PID 控制的单位阶跃响应指标，如表5、表6 所示。

表5 位置PID 与模糊PID 控制单位阶跃响应性能指标

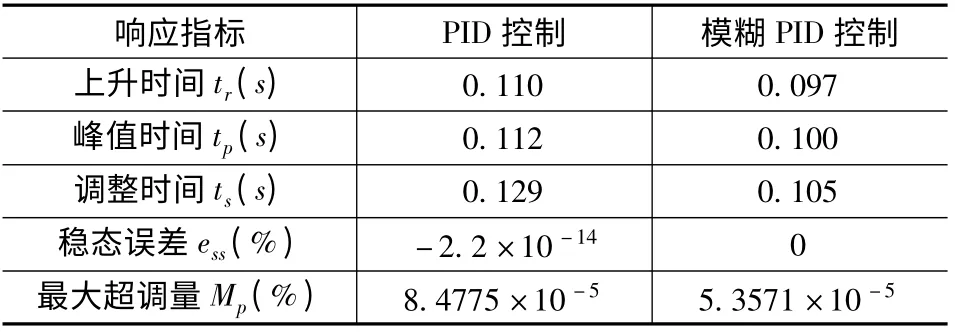
表6 速度PID 与模糊PID 控制单位阶跃响应性能指标

3.2 系统加干扰单位阶跃响应仿真分析

CNC 粉末液压机电液伺服控制系统在实际工作过程存在各种扰动的影响，因此，抗干扰性能是衡量系统控制性能需考虑的一项重要因素。为了验证模糊PID的抗干扰能力，保持PID 参数和模糊PID 控制器参数不变，分别在PID 与模糊PID 控制的单位响应阶跃过程中加入随机干扰(干扰在第1s 加入，干扰的持续时间为0.1s)，则位置、速度的PID 控制与模糊PID 控制的单位阶跃响应分别如图6、图7 所示。

图6 位置PID 与模糊PID 的加干扰单位阶跃响应

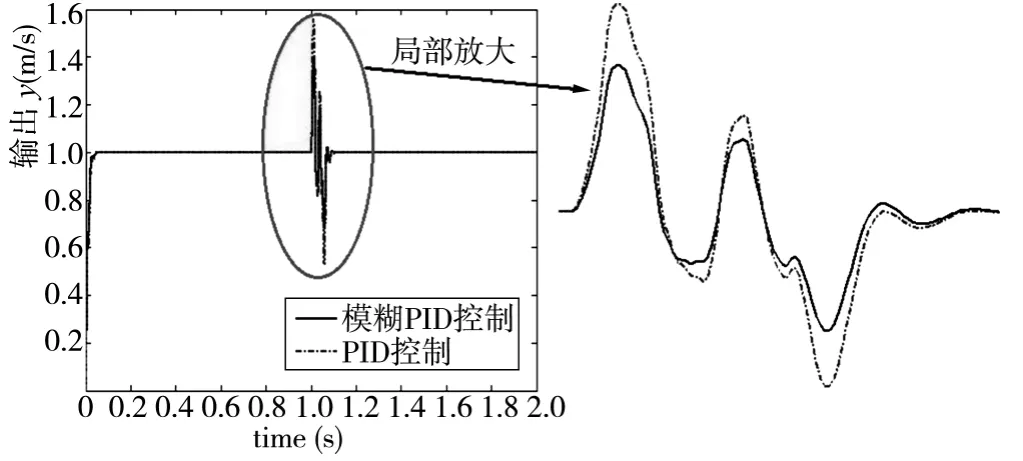
图7 速度PID 与模糊PID 的加干扰单位阶跃响应

由图6 可以看出，在加入干扰后，位置PID 控制的波动幅度明显大于位置模糊PID 控制，并且位置模糊PID 控制克服干扰重新回到稳定状态所需要的时间(约0.3s)也小于位置PID 控制克服干扰重新回到稳定状态所需要的时间(约0.5s)。从图7 可以看出，在加入干扰后，速度PID 控制的响应过程发生了剧烈的振荡，而速度模糊PID 控制虽然也发生了振荡，但振荡的幅度小，并且重新回到稳态所需的时间短，能够较快的消除干扰引起的抖振，并且在回到稳态的过程中系统没有持续波动，表现出了良好的抗干扰性。

3.3 系统参数变化仿真结果对比分析

由于电液位置伺服系统参数的时变性，特别是液压阻尼比ξh是一个不容易准确计算的参数，并且变化范围大。为了验证模糊PID 对时变系统的自适应性，保持PID 参数和模糊PID 控制器参数不变，假设CNC粉末液压机电液控制系统的阻尼比ξh由0.2 变化为0.6，则得到ξh变化后系统的位置与速度开环传递函数分别为式(5)、式(6)所示。

分别对式(5)、式(6)进行单位阶跃响应，则可得系统阻尼比ξh发生变化后的位置、速度的PID 控制与模糊PID 的单位阶跃响应情况。位置的PID 控制与模糊PID 控制的单位阶跃响应如图8 所示，速度的PID 控制与模糊PID 控制的单位阶跃响应如图9 所示。

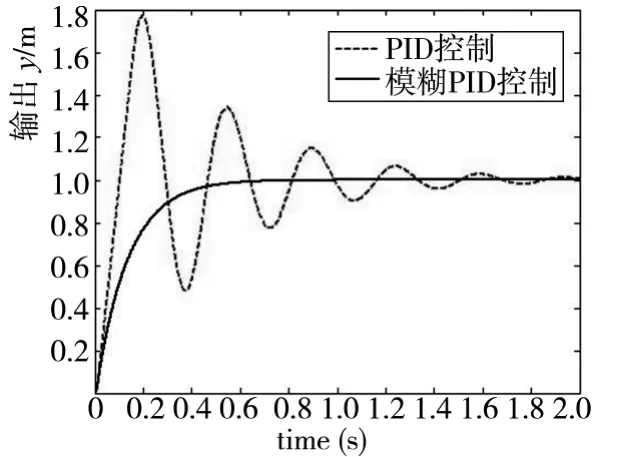
图8 系统阻尼比改变后位置PID 与模糊PID 控制的单位阶跃响应

图9 系统阻尼比改变后速度PID 与模糊PID 控制的单位阶跃响应

由图8 可以看出，当系统阻尼比ξh改变时，位置模糊PID 控制器仍然能够保持良好的控制性能，具体表现:在单位阶跃响应过程中，系统没有超调和振荡，整个响应过程平滑稳定。而这时的位置PID 控制器由于不能够自适应的调整其PID 控制参数，位置PID 控制器已经不能对系统进行有效控制了，出现了持续的振荡，系统表现出很强的不稳定性。从图9 可以看出，当系统参数ξh改变时，速度PID 控制在响应过程中出现了振荡，具有较大的超调量。而速度模糊PID 控制具有自适应的调整PID 的参数特性，因此仍然能够具有良好的控制性能。

4 结束语

(1)针对粉末冶金数控液压机的电液位置伺服系统具有时变性、强干扰等特性，而常规PID 控制器对这样的系统又难以达到理想的控制效果，因此设计了模糊PID 控制器对系统进行自适应控制。

(2)为了验证模糊PID 与PID 控制的对比效果，分别用模糊PID 控制与PID 控制对粉末冶金液压机的电液伺服系统进行仿真分析。仿真结果表明:在系统正常工作状态(即无干扰，无参数时变)下，模糊PID比常规的PID 控制具有更好的控制性能，但其控制性能的优越性并不是很明显;在系统有干扰的状态下，与常规PID 控制相比，模糊PID 具有良好的抗干扰能力;在系统阻尼比ξh发生变化的状态下，由于模糊PID 控制器具有自适应调整其PID 参数的特性，仍然对系统具有良好的控制能力，表现出了很强的自适应控制性能，而这时常规PID 对系统的控制能力有较大的下降，甚至控制系统出现不稳定的现象。因此，综合常规PID 控制与模糊PID 控制的单位阶跃响应的情况，模糊PID 控制器比常规PID 控制器具有更优的控制性能。

［1］胡包钢，应浩. 模糊自适应PID 控制研究发展回顾及其面临的若干重要问题［J］. 自动化学报，2001，27(4):567－581.

［2］关景泰. 机电液控制技术［M］. 上海:同济大学出版社，2003.

［3］高钦和，龙勇，马长林，等. 机电液一体化建模与仿真技术［M］. 北京:电子工业出版社，2012.

［4］曾光奇，胡均安，王东，等. 模糊控制理论与工程应用［M］. 武汉:华中科技大学出版社，2006.

［5］田凡. 电液伺服系统模糊PID 控制仿真与试验研究［D］.太原:太原理工大学，2010.

［6］张化光，孟祥平. 智能控制理论及应用［M］. 北京:机械工业出版社，2005.

［7］韩江，余仲元，何高清，等. 模糊自适应PID 控制在数控精密校直机电液伺服系统中的应用研究［J］. 组合机床与自动化加工技术，2009(8):54－56.

［8］Oysal Y.，Koklokaya E.，Yilmax A.S..Fuzzy PID controller design for load frequency control using gain scaling technique［J］. International conference on Electric Powder Engineering，1999:178.

［9］Wang ning. A fuzzy PID controller for mutil－model plants［J］. Proceedings 2002 International Conference on Machine Learning and Cybernetics，2002(3):1401－1404.

［10］张建民，王涛，王忠礼. 智能控制原理及应用［M］. 北京:冶金工业出版社，2003.