滚珠丝杠副滚珠循环系统的热机耦合分析
2013-12-23李登新
赵 萍,李登新
(莱芜职业技术学院,山东 莱芜 271100)
0 引言
随着数控机床向高速化、高精度化方向不断发展,对高速精密滚珠丝杠的制造水平提出了更高要求。滚珠在返回器中循环运动,特别是在高速情况下,滚珠对返向器的冲击会引起较大的振动和热量,影响滚珠丝杠副的使用寿命[1-3]。国外学者Hung等[4]利用赫兹接触模型建立了滚珠与导珠管碰撞的力学模型,利用有限元软件分析研究了导珠管的疲劳问题。Braccesi 等[5]利用滚珠与导珠管碰撞的力学模型和材料的弹塑性理论估计了不同材料的滚珠循环系统允许的最高转速。国内宋宪春[6]根据赫兹接触模型和经典碰撞理论,建立了滚珠与返向器碰撞接触的力学模型,导出了碰撞力公式,并在考虑弹性恢复系数的基础上推导出了碰撞接触时间公式。上述学者分析了碰撞过程中的力及作用时间,没有分析碰撞过程中的温度及热机耦合现象,因此分析是不全面的。
冲击滑动接触主要表现为反复的热冲击和剪切,随着碰撞过程的进行,整个表面的温度会逐步升高。接触过程中表面温度的变化,对于摩擦、磨损过程有很大影响。本文建立了冲击滑动耦合作用下的接触模型,利用有限元法建立了返回期内滚珠在冲击滑动耦合作用下二维摩擦滑动接触计算模型,研究了该工况下的摩擦热效应及热-机耦合应力分布。
1 滚珠与导珠管碰撞接触理论模型
无摩擦弹性体之间撞击的经典理论是由Hertz提出的,并直接从他的静力弹性接触理论中得出[7-8]。两个弹性球,半径分别为R1和R2,质量分别为m1和m2,以相对速度V 对心撞击。图1 所示为滚珠与返回器碰撞简化模型。

图1 滚珠与返回器碰撞简化模型
随接触时间的变化,对心碰撞球之间接触力为:

式中:F(t)接触力(N);δs(t)冲击碰撞过程中弹性球中心的法向变形量(mm);

其中,E1、E2、μ1、μ2分别是钢球、导珠管材料的泊松比和弹性模量。
根据牛顿第二定律可得:

代入(1)式可得:


在最大压缩δmax时=0,可求出最大压缩为:


忽略波动中吸收的能量,认为变形可以恢复的。碰撞的总时间为:

2 热-机耦合模型
当摩擦副间发生较大相对滑动时,会产生很强的摩擦热源[9]。接触区内由摩擦导致的热源热流密度分布可按下式求得[10]:

式中qf热流密度分布;μ 接触面间摩擦系数;p(x,t)接触法向压力分布(MPa);vs摩擦副间相对滑动速度(mm/s);η 摩擦功与热的转换率。
滚珠丝杠副滚珠循环系统自由边界与环境之间存在着热交换,交换方式为热对流和热辐射。在计算中两种传热方式都按第三类边界条件来处理,即用表面传热系数h 来模拟块试件表面与外界环境的热交换[11]。其数学表达如下:
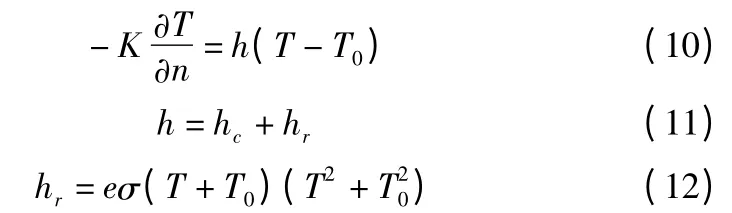
其中,n 自由边界的单位外法向向量;hc、hr自由表面与环境的热对流换热系数和热辐射换热系数,其中,取hc=0.028W/(m2* K);e 发射率,取0.3;σ 斯蒂芬-玻尔兹曼常数,取5.67 ×10-11mW/mm2K4;T 自由边界温度(℃);T0环境温度,取20℃。
以下列规格的滚珠丝杠副为例分析:滚珠丝杠副的公称直径为40mm,滚珠的直径为4.763mm,导珠管的外直径为7.0 mm,内径为5.26mm,弯曲半径为11.5 mm。参考表1 中滚珠和导珠管材料的物理属性,分别对碰撞力和碰撞接触时间做出计算[12]。

表1 滚珠与返回器相应材料的属性表
3 结果分析
数值模拟过程采用有限元软件ABAQUS 的Standard 求解器计算。有限元模型如图2 所示,计算本模型采用显式求解的最大时间增量数量级为10-9s,在一个冲击周期内的增量步就可达百万次,计算时间过长,故采用无条件稳定的隐式方法求解[13],钢球冲击后,返回器内应力云图如图3 所示。
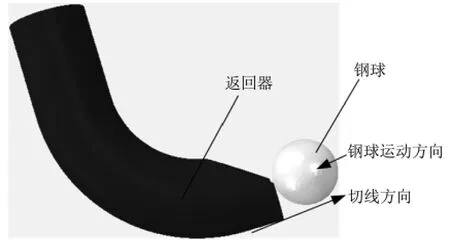
图2 滚珠丝杠副滚珠循环系统有限元模型

图3 返回器内应力云图
3.1 摩擦过程中的热效应
在冲击滑动接触过程中,返回器接触区中心始终处于接触状态,接触应力最大,故温度最高。图4 为冲击频率为45Hz 时一个冲击周次下接触区中心节点的温升曲线。由于摩擦生热,接触区中心节点的温度急剧升高,达到最高点后由于返回器中的热传导及与外界介质的对流辐射,温度迅速下降。滑动速度对温升影响很大,滑动速度v = 5. 0m/s 时,中心节点瞬态最高温度为51. 4℃;当滑动速度v =0. 5m/s 时,中心节点瞬态最高温度为7. 1℃。
在滑动速度较大时,每个冲击周次后中心节点会存在较大的残余温度。图5 和图6 为首次冲击后不同冲击频率及滑动速度下接触区中心节点残余温度曲线。图5 中,随着滑动速度的增加,残余温度呈上升趋势,这是由于随着滑动速度的增加,由于摩擦产生的热流密度也随之增加,进而导致残余温度升高。由图5 同时可以看出,随着冲击频率的增加,残余温度值曲线的斜率随之增加。图6 中,当滑动速度一定时,随着冲击频率的上升,接触区中心残余温度也随之增加。在较低冲击频率下,由于每个冲击周次的时间间隔大于较高冲击频率下的时间间隔,因此摩擦生热有更多的时间向接触区附近发生热传导并与空气介质发生对流与辐射散热。这说明,较高的冲击频率更容易导致接触区摩擦生热的积聚。

图4 一次冲击周期下接触区中心节点的温升

图5 不同冲击频率下接触区中心节点残余温度

图6 不同滑动速度下接触区中心节点残余温度
3.2 冲击滑动作用下的热-机耦合作用
图7 为冲击频率70Hz,在不同滑动速度下接触面沿x 方向的应力σx分布。最大冲击力幅值70N,摩擦系数0.25。由于存在切向摩擦力,σx呈不对称分布,当σx>0 时为拉应力,σx<0 时为压应力。
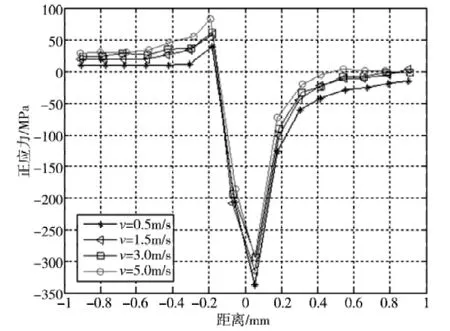
图7 不同速度下接触面x 方向正应力分布
最大拉应力出现在接触区边缘,冲击过程中,由于接触区域不断变化,接触区中心左侧承受交变的拉压作用,这种交变的应力作用使接触面易于产生疲劳裂纹,加速磨损。随着滑动速度的增加,接触区左侧的拉应力σx逐渐减小,右侧的压应力σx逐渐增大。
图8 为冲击频率70Hz,在不同摩擦系数条件下接触面沿x 方向的正应力σx分布。最大冲击力幅值70N,滑动速度3.0m/s。如图所示,σx呈不对称分布,最大拉应力出现如图所示,σx呈不对称分布,最大拉应力出现在接触区边缘。随着摩擦系数的增加,最大压应力的位置由接触区中心向右侧逐渐偏移,而单纯的摩擦热效应并未使最大压应力发生偏移,这表明切向摩擦力对接触面σx的分布有较大的影响。随着摩擦系数的增加,接触区左侧的拉应力σx逐渐减小,右侧的压应力σx逐渐增大。这是由于当摩擦系数增大时,摩擦生热加剧,接触区表面的温度梯度变大,热应力在接触区左侧会降低接触区表面x 方向的拉应力,在接触区右侧将增加x 方向的压应力,同时,增大的摩擦系数会产生更大的切向摩擦力,切向摩擦力会加剧这一变化趋势。接触区边缘交变的拉压作用。
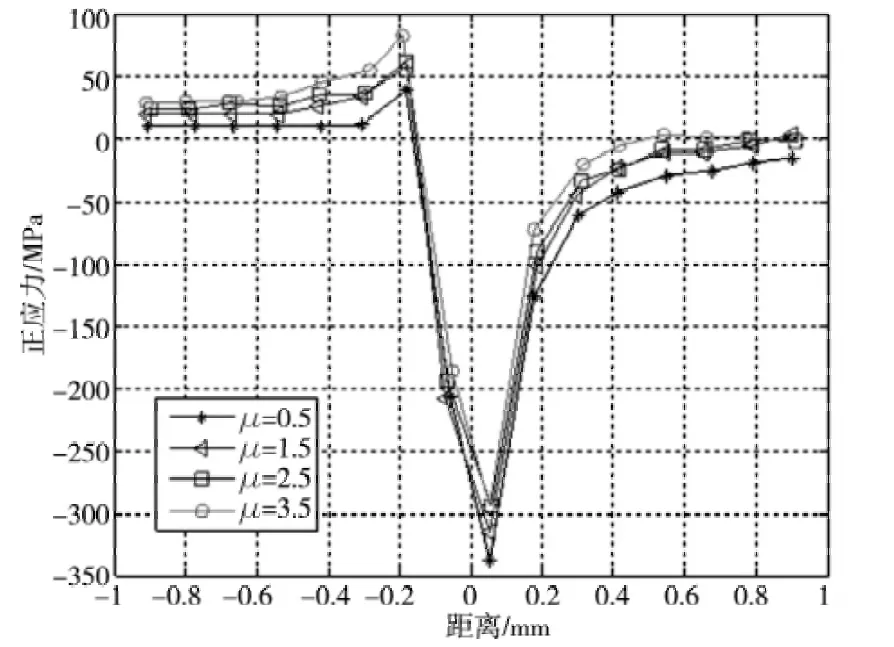
图8 不同摩擦系数下接触面x 方向正应力分布
图9 为冲击频率70Hz,在不同滑动速度下接触面的等效应力分布。最大冲击力幅值70N,摩擦系数0.25。当考虑热效应时,等效应力不再呈对称分布,随着滑动速度的增加,不对称度趋于显著。同时可以看出,热效应并没有加剧接触区表面的等效应力水平,相反在一定程度上降低了接触区表面的等效应力。由于热效应,最大等效应力点随着滑动速度的增加逐渐向接触区右侧移动,在速度为5.0m/s时,最大等效应力点位于接触区边缘。
4 结论
由于冲击滑动接触中摩擦副间的瞬态相互作用,对材料产生强烈的热冲击,当滑动速度较大时,热冲击变得非常剧烈。每个冲击周次后接触区会存在较大的残余温度。较高的冲击频率更容易导致接触区摩擦生热的积聚。由于摩擦产生的热应力与机械应力叠加,在接触区左侧会降低接触区表面x 方向的拉应力,在接触区右侧将增加x 方向的压应力。切向摩擦力对接触表面x 方向的正应力分布有较大的影响。热影响区很薄,仅在表层至表层下方发生较大作用。热效应并没有增加接触区表面及沿深度方向分布的等效应力,但增加了沿深度方向分布的等效应力梯度。热-机耦合作用下,最大等效应力比纯机械作用下的最大等效应力更接近接触表层。
[1]张佐营,宋现春,姜洪奎. 滚珠丝杠副中滚珠与返向器的碰撞研究[J]. 中国机械工程,2008,19(7):850-854.
[2]黄浩,陈志雄. 基于RECURDYN 的滚珠丝杠循环系统动力学仿真[J]. 湖北汽车工业学院学报,2007,21(4):17-21.
[3]魏勇强. 冲击滑动耦合作用下高速轴承与密封材料磨损行为的研究[D]. 哈尔滨工业大学,2010.
[4]Hung J P,Wu J S,Chiu J P.Impact Failure Analysis of Recirculating Mechanism in Ball Screw[J].Engineering Failure Analysis,2004,11:561-573.
[5]Braccesi C,Landi L. A General Elastic-plastic Approach to Impact Analysis for Stress State Limit Evaluation in Ball Screw Bearings Return System[J]. International Journal of Impact Engineering.2007,34(7):1272-1285.
[6]宋现春,姜洪奎,张佐营. 滚珠丝杠副中滚珠与导珠管的接触碰撞分析[J]. 江苏大学学报,2008,29(5):373-375.
[7]剧锦三,蒋秀根,傅向荣. 考虑接触变形的梁受到球碰撞时弹塑性冲击荷载[J]. 工程力学,2008,25(4):32-38.
[8]康献民,王大承,王天雷. 精密丝杠副中滚珠冲击及其影响因素研究[J]. 五邑大学学报(自然科学版),2009,23(4):1-9.
[9]龙慧,张光辉,罗文军. 旋转齿轮瞬时接触应力和温度的分析模拟[J]. 机械工程学报,2004,40(8):24-29.
[10]赵凯辉,魏朗. 鼓式制动器三维热-机耦合温度场仿真[J]. 农业机械学报,2009,40(2):32-36.
[11]戴锅生. 传热学[M]. 北京:高等教育出版社,2001.
[12]姜洪奎,宋现春. 滚珠丝杠副滚珠循环系统的动力学研究和仿真[J]. 振动与冲击,2009,26(3):107-113.
[13]石亦平,周玉蓉. ABAQUS 有限元分析实例详解[M].北京:机械工业出版社,2010.
