基于特征的制造资源分类方法的研究*
2013-12-23赵昌龙关雪松
赵昌龙,关雪松
(1.长春大学 机械与车辆工程学院,长春 130022;2. 吉林大学 机械科学与工程学院,长春130022)
0 引言
针对目前市场需求的不可预测、持续发展和快速多变性,企业的各类生产活动也必须相应的具有高柔性,以便能够对市场需求的变化做出快速的反应,并且及时对其自身的生产做出合理的调整甚至是重新规划生产活动。虚拟制造[1-2]则是解决这一问题的有效途径,利用虚拟制造技术在企业现有制造资源条件下,对产品模型的各个设计属性满足制造约束的程度进行系统的分析,进而得到设计模型中对产品制造和产品质量不利的因素,从而及时地指导研发人员进行该产品的设计。
企业的制造资源主要包括企业的各种加工设备,而一个加工设备则可能具备多个加工特征,不同加工设备的工艺能力差别也越来越小,因此,为了在可制造性评价过程中缩短搜索的时间、降低成本并且使这些设备便于管理,本文针对不同设备的加工特征,利用遗传算法和模糊聚类算法对其进行有效的分组。
1 混合聚类算法的组成
将遗传算法与FCM 算法[6-8]相结合,不仅能够发挥遗传算法的全局寻优能力,而且可以兼顾FCM 的局部寻优能力,有效的克服FCM 对初始化的敏感度,提高收敛速度,解决聚类问题具有更好的效果。基于遗传算法和遗传模糊聚类算法的混合聚类算法由外层迭代和内层迭代两大部分构成[9-12],外层迭代利用遗传算法(GA)动态来获得最佳分类数,内层迭代则利用遗传模糊聚类算法(FGCM)进一步确定与最佳分类数相对应的最优分类,将内层迭代嵌入到外层迭代之中。
在加工过程中,由于零件及其被加工特征的尺寸与精度等制造标准的要求不同,即使是同一类型的特征往往也需要采用不同的加工设备进行加工,因此在加工设备分组过程中,除了考虑加工设备所能够完成的加工特征外(包括柱锥、平面、槽、孔、曲面和阶梯),将机床的加工能力(包括机床所能加工零件的尺寸大小及加工精度)也作为分组的依据,即将加工设备是否能加工大中型零件、是否能进行精加工也作为加工设备的属性在基于工艺的加工分组中,零件加工设备可用向量xi表示:

假如某立式铣床可以加工平面、曲面和槽等特征,而且可以进行大中型零件的精加工,则它可以用特征向量(011010 01)来表示,如图1 所示。

图1 加工设备向量
1.1 内层迭代
内层循环主要是利用遗传模糊聚类算法在对应类别数c 下进行的全局寻优,以获得最优分类。解决聚类问题的时候用到遗传算法,应该主要考虑到如何对聚类问题进行染色体编码、如何构造个体适应度评价函数,以及遗传算子和遗传参数设置等问题。
1.1.1 染色体编码方案
在这里,聚类中心矩阵V 采用实数编码方案。我们可以假设:将n 个加工设备分成c 类,也就是说将一条染色体看成是由c 个聚类中心vi(i=1,2,…c)所组成的一个串,如果每个聚类中心有s 个特征,则这条染色体就是一个长度为c×s 的实数码串
chr:
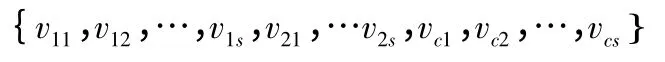
1.1.2 适应度函数构造
聚类问题实际上也可以看做是一个优化问题,也就是将待聚类数据集的损失函数达到最小化,即聚类效果越好,目标函数越小,而对应的适应度函数应该越大。利用FCM 算法目标(损失)函数Jm定义适应度函数为:
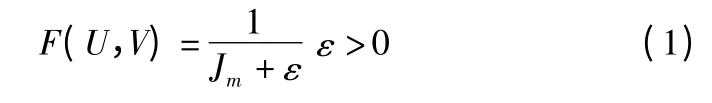
1.1.3 遗传算子
选择算子采用最优个体保存策略与无回放余数随机选择相结合的混合遗传算子。无回放余数随机选择的优点在于能够保证适应度高的个体一定能够遗传到下一代的群体中,选择误差较小;最优个体保存策略则可以保证遗传算法的全局收敛性。
选择算子为双点交叉算子,在个体编码中采用随机方式设置两个交叉点,然后对基因进行部分交换,变异操作采用均匀遗传算子来完成。
1.1.4 个体的FCM 优化
根据每条染色体的聚类中心编码,在每一代执行完遗传操作后对其进行FCM 优化,分别更新聚类中心V 和模糊矩阵U。将新的聚类中心矩阵编码成为新的染色体,并且重新计算目标函数值,采取最优个体保存策略。
1.2 外层循环
FCM 算法在聚类分析前需要对分类数量进行设定,不能对子类数量进行优化,在外层循环中可以利用遗传算法动态确定最佳分类数。效果好的聚类算法不仅要考虑模糊划分同一类中的紧凑程度,而且要考虑不同类之间的分离程度。用类间距D 来表示各聚类中心之间的欧式距离的平均值,它表示出各聚类中心之间的离散程度,D 值越大说明不同类之间的分离程度越大,由公式(2)可以计算得出D 值:
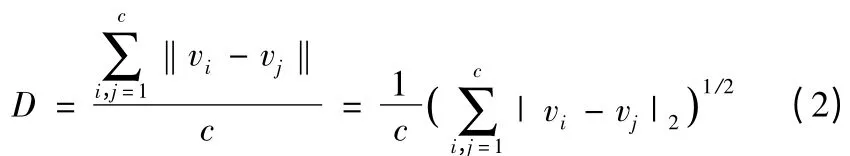
外层迭代的目标就是将聚类损失函数Jm 最小化,而类间距离D 尽可能的大。定义外层迭代的目标函数如下:

通过变换,可以将求最小值问题转化为求最大值的问题,从而得到外层遗传算法的适应度函数:
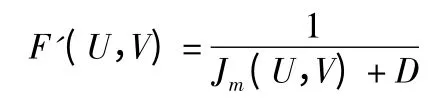
对分类数所进行的二进制编码,采用最优保存策略和无回放余数随机选择相结合的混合遗传算子,利用单点交叉和基本位变异算子进行遗传操作,在对应的分类数c 下,再利用内层循环,得到与类别数c 对应的最优分组。混合算法的流程图如图2 所示。
2 实例分析
内部循环群体个数为40,外部循环的群体个数20,交叉概率和变异概率分别为0.8 和0.1,将100次作为终止条件为。与不同的分类数对应的模糊聚类的损失函数Jm 和类间距D 如图3 所示,由图3 可以看出分类数为6 时,Jm 与D 的和最小,此时外部循环的适应度函数值最大,也就是说6 为最佳分类数。当分类数为6 时,分类结果如表2 所示。
为了验证混合模糊聚类算法的有效性,对22 个加工设备进行分组,设备的属性包括柱锥、平面、孔、槽、曲面、阶梯、是否能加工大中型零件和是否能用于精加工等八个属性,设备及其属性如表1 所示。
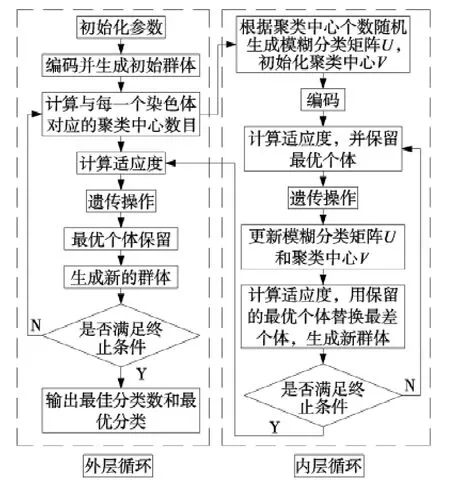
图2 混合算法流程图
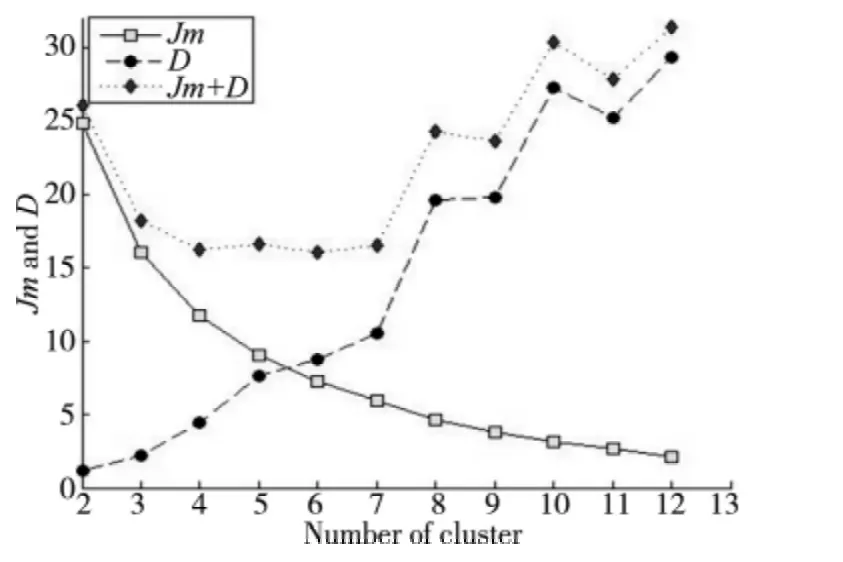
图3 模糊聚类的目标函数值图
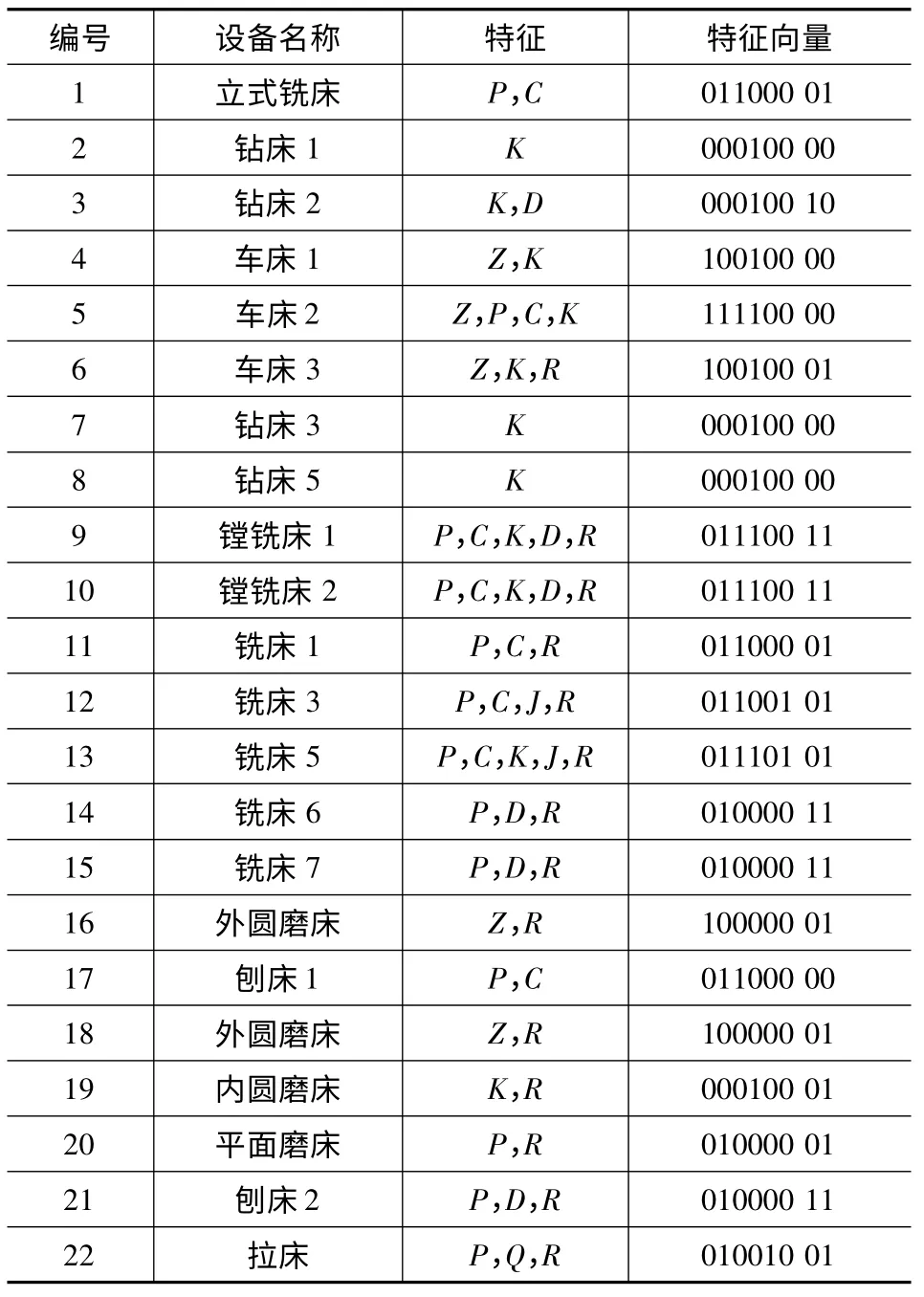
表1 加工设备及其属性
表1 中:Z、P、C、K、Q、J、D 和R 分别表示柱锥、平面、槽、孔、曲面、阶梯、是否能加工大中型零件和是否能用于精加工等设备特征。
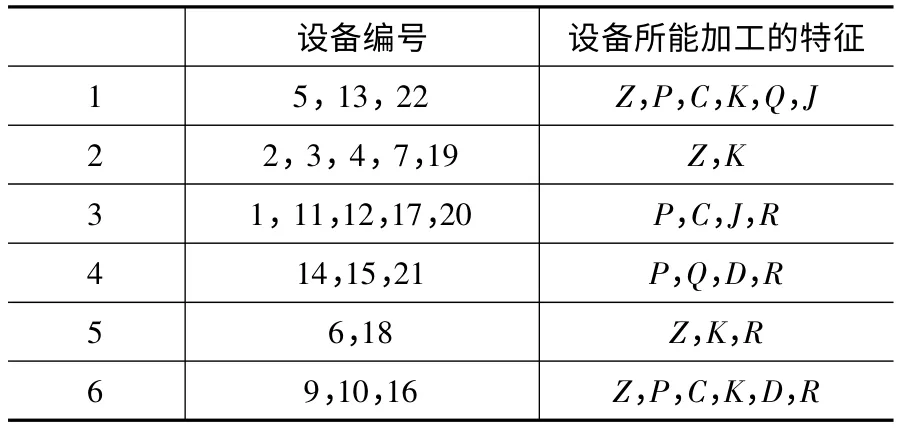
表2 分类结果
第一组中的加工设备和第六组中的加工设备同样都能加工柱锥、平面、槽和孔,但是第六组加工设备可以用于大中型零件的精加工,如果所加工的零件为大中型零件则可以直接搜索第六组加工设备,减少搜索时间和空间。在第二组、第一组和第六组中,设备的属性中都有孔特征,但是在一个零件不仅需要加工一个孔特征,还需要加工其他的特征时,如平面、槽和曲面等特征时,选用第二组和第六组中的加工设备,使零件在一次装夹中可以进行多个特征的加工,这样更有利于保证零件的加工质量和减少装夹的时间。
3 结束语
本文提出了一种基于模糊C-均值聚类算法和遗传算法的混合算法,并应用这一混合算法进行加工设备的分类,利用这种方法可以动态的确定分类数和分类。在实例分析中以22 种加工设备为例,根据不同加工设备的加工能力对加工设备进行了分组,分组情况符合实际应用,利用这种方法,可以有效地减少加工设备的搜索时间,提高加工效率。
[1]Mariella Consoni,Florenzano Souza,Marco Sacco,Virtual manufacturing as a way for the factory of the future[J].Journal Intelligent Manufacturing,2006,17:1-24.
[2]Kimura F,Product and Process Modeling as a Kernel for Virtual Manufacturing Environment[J]. Annals of the CIRP,1993,42(1):147-150.
[3]Onosato M,Iwata K,Development of a virtual manufacturing system by integrating product models and factory models[J]. Annals of the CIRP,1993,42(1):475-478.
[4]Zhang T,Ramakrishnan R,Livny M,Birch:a new data clustering algorithm and its applications[J]. Data Mining and Knowledge Discovery,1997,1(2):141-182.
[5]Wu K. L,Yang M. S. Alternative C-meansclustering algorithms[J]. Pattern recognition,2002,35:2267-2278.
[6]Zhang D.Q,Chen S.C. A novel kernelized fuzzy C-means algorithm with application in medical image segmentation[J]. Artificial Intelligence Med.,2004,32:37-50.
[7]Fan J L,Zhen W.Z.Suppressed fuzzy c-means clustering algorithm[J].Pattern Recognition Lett.,2003,24:1607-1612.
[8]Karayiannis N B.Generalized fuzzy c-means algorithms[C].In:Proc.Of the 5th IEEE Int’1 Conf.on Fuzzy Systems,2:1036-1042,New Orleans:IEEE,1996.
[9]Azzag H,Ventrini G,Oliver A,A hierarchical ant based clustering algorithm and its use in three real-world applications[J]. Eur. J. Oper. Res,2007,197(3):906-922.
[10]Azzag H,Monmarche N,Slimane M,A clustering algorithm based on the ants self-assembly behavior[C]. In:Advances in Artificial Life-Proceedings of the 7th European Conference on Artificial Life,Dortmund,Germany,2003,2801:564-571.
[11]Ngai E. W. T,Chan E. W. C. Evaluation of knowledge management tools using AHP[J]. Expert Systems with Application,2005,29:889-899.
[12]Soremekun G,Gürdal Z. Composite laminate design optimization by genetic algorithm with generalized elitist selection[J]. Computers and Structures,2001,79:131-143.
