R中数字集的刻画

相中启，简辉华

(1.华中师范大学数学与统计学学院，中国武汉 430079;2.新余学院电气与电子工程学院，中国新余 338004)

设b ≥2 是一整数，D={d0，…，db－1}⊂R 是数字集，则数字对(b，D)定义了一迭代函数系统

φi(x)=b－1(x+di)，0 ≤i ≤b－1.

这些映射显然是压缩映射，因此存在唯一的非空紧集T=T(b，D)使得［1－2］.该集合方程的一个等价形式为

更确切地，我们可以将T 中的元素表示成关于基b 及数字集D 的基数展式，即

如果T· ≠∅，我们称T=T(b，D)是自相似tile，D 为自相似tile 数字集.这个条件等价于，也等价于T 的Lebesgue 测度m(T)＞0［3］.

设T=T(b，D)是自相似tile，则L2(T)中的内积规定为

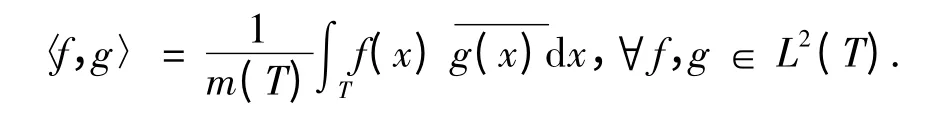
对于数字集的研究，我们最关心的是那些可以生成自相似tile 的数字集，最简单的形式由Bandt 给出［4］:若D 是模b 完全剩余系，则T(b，D)是自相似tile.我们称这样的数字集为标准数字集.特别地，如果b 是素数，Kenyon 在文［5］中给出如下结论:

T(b，D)是自相似tile 当且仅当D 是模b 完全剩余系.

对于D 不是标准数字集的情形，最重要的是积形式的数字集，这一形式的数字集由Odlyzko 引入［6］，用于研究实数关于基b 的基数展式，而后Lagarias 与汪洋在文［7］中给出其正式定义:

如果D=ε0+bl1ε1+…+blkεk，其中ε=ε0⊕ε1⊕…⊕εk是模b 完全剩余系，0 ∈εi(0 ≤i ≤k)，0 ≤l1≤l2≤…≤lk，则称D 为积形式数字集.再者，如果ε={0，1，2，…，b－1}，那么称D 为严格积形式数字集.

他们证明了:如果D 是积形式的数字集，则T(b，D)是自相似tile.

Kenyon 给出了一个研究自相似tile 数字集的重要工具，称为Kenyon 准则.该准则已被广泛应用于研究自相似tile 数字集及相关课题［7－9］.何兴纲与刘家成［9］推广了Protasov［10］关于最小切集的定义，建立了紧集的概念，受此启发，本文给出了一种研究自相似tile 数字集的新方法.

1 自复制tiling 集

设T 是T=T(b，D)的tiling 集，若T=bT+D，则称T 是自复制的.刘家成和饶辉［8］加强了Kenyon 在文［11］中的结果，得到:

定理1［8］设0 ∈D ⊂Z 且D 中的元素互素.如果T=T(b，D)是自相似tile，则

(1)存在唯一的自复制tiling 集T 具有性质:0 ∈T ⊆Z，存在m ≥0 使得T=T+bm.

(2)若S ⊆Z 是周期的且S=bS+D，则(T，S)是一tiling 对且S=T.

注1上述结果中唯一性的获得需要假定0 ∈T 或者T ⊂Z，如果无此假设，则自复制tiling 集可能不唯一.例如，b=3，D={0，1，2}，则T=［0，1］，因此Z 与均是T 的自复制tiling 集.

引理1［5］设D={d0，…，db－1}⊂Z+，则D 是自相似tile 数字集的充分必要条件是对任意整数m ≠0，存在k ≥1 使得，其中.

定理2设T=T(b，D)是自相似tile，T 是其唯一的自复制tiling 集，则{eλ:eλ(x)=e2πiλx，λ ∈T}是L2(T)中的规范正交集.

证令，对T 上的特征函数XT作Fourier 变换，则对任意k ≥1 有

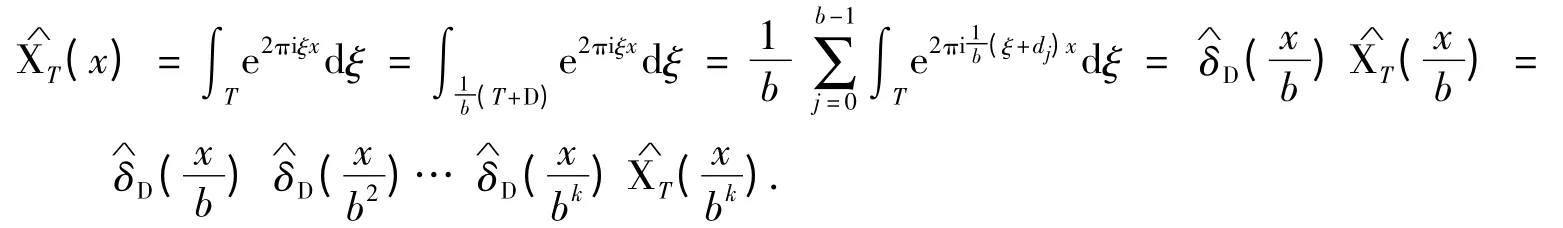
对任意λ，γ ∈T，λ ≠γ，由引理1 知，存在k ≥1 使得，因此

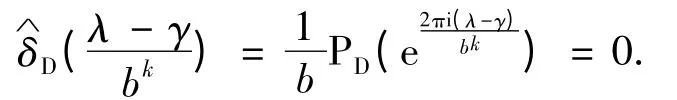
如果D 是模b 完全剩余系，Lagarias 等［12］证明了T(b，D)有格tiling.该结论中的假设条件不能减弱，事实上即使D 是严格积形式，T(b，D)也可能没有格tiling.例如，若b=4，则D={0，1，8，9}={0，1}+4{0，2}.因此D 是严格积形式，且ε0={0，1}，ε1={0，2}，ε={0，1，2，3}.易见T(b，D)=［0，1］∪［2，3］，因此T(b，D)没有格tiling，但有2 个不同的周期tilings，即

T={j+4Z:j=0，1}，T'={j+4Z:j=0，3}.

定理3设D={d0，…，db－1}是严格积形式.如果b 是素数，则T(b，D)有格tiling T，并且T 是自复制的.

证由严格积形式的定义，∀ej∈ε 有唯一分解

ej=ej，0+ej，1+…+ej，k，ej，i∈εi，0 ≤i ≤k.

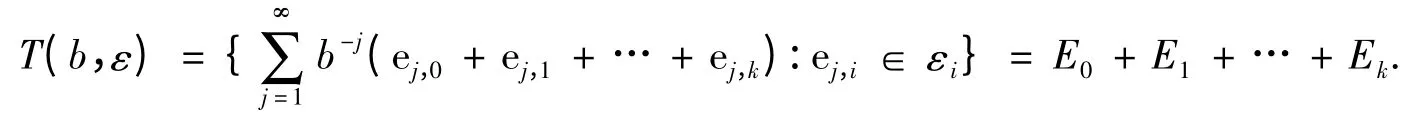
由于∀dj∈D 也有唯一分解:dj=ej，0+bl1ej，1+…+blkej，k，因此有

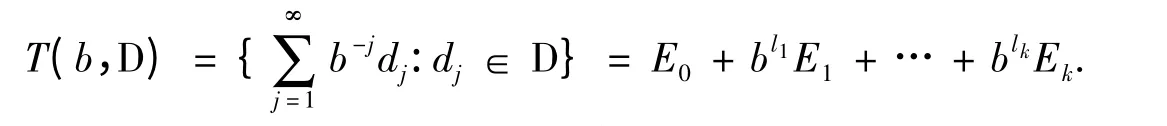
注意到blkEi=Ei+Ai，lk，其中，若k=0，则规定Ai，lk={0}.于是

T(b，D)=E0+(E1+A1，l1)+…+(Ek+Ak，lk)=(E0+E1+…+Ek)+(A1，l1+…+Ak，lk)=T(b，ε)+(A1，l1+…+Ak，lk)=［0，1］+(A1，l1+…+Ak，lk).

因为b 是素数，则或者D={0，1，…，b－1}，此时T(b，D)=［0，1］有格tiling T=Z，且T=bT+D，即T 是自复制的;或者存在m，1 ≤m ≤k，使得D=blm{0，1，…，b－1}.所以

T(b，D)=［0，1］+Am，lm=blm［0，1］.

由于T(b，D)+blm(［0，1］+Z)=blmR=R，因此T(b，D)有格tiling T=blmZ.易见bT+D=blm(bZ+{0，1，…，b－1})=blmZ=T，所以T 是自复制的.

2 C－紧集

设C={c0，c1，…，cm}⊂Z.令φj(x)=b－1(x+cj).利用压缩映射系统来定义树结构:令α0=0，αk=φjk(αk－1)=b－1(αk－1+cjk)，cjk∈C 表示第k 次迭代的衍生物.我们称这样的αk为一个C－状态.易见αk=b－kcj1+…+b－1cjk.令表示所有的

对一有限序列{cj0，cj1，…，cjk}，令α0=0，αk=b－kcj1+…+b－1cjk，1 ≤k ≤n，称相应的有限状态列γ=为一条从0 到αn的路径，无穷路径可类似定义.

定义1设C={c0，c1，…，cm}⊂Z.令P 表示所有包含无穷多个不同状态的路径的集合，若满足

(1)0 ∉N;

引理2设D={d0，…，db－1}是自相似tile 数字集，则对任意非零整数

证由定理2 知

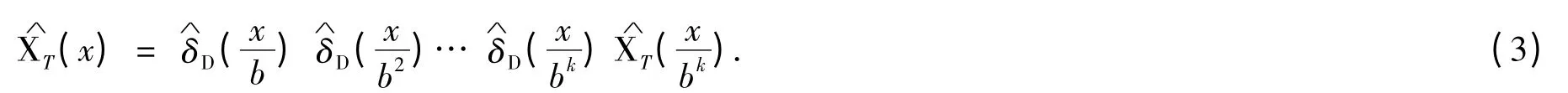
对任意整数m ≠0，令r=bkm，则对所有的)，由(3)式，.因为T 是自相似tile，故XT是有紧支撑的L1函数，由Riemann-Lebesgue 引理知，

定理4设D{d0，…，db－1}⊂Z，则D 是自相似tile 数字集当且仅当对任意的数字集C={0=c0，c1，…，cm}⊂Z，m ≥1，存在紧集N 使得∀a ∈N，PD(e2πia)=0.

证先证必要性.设D 是自相似tile 数字集，XT是自相似tile T=T(b，D)上的特征函数，则

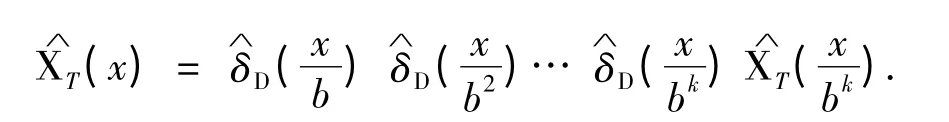
对任意给定的数字集C={0=c0，c1，…，cm}⊂Z，m ≥1，任意路径，考虑那些使得0 ≠vk=bkαk∈Z 的αk，则vk=cj1+…+bk－1cjk.由的整周期性，对所有的l ≤k，

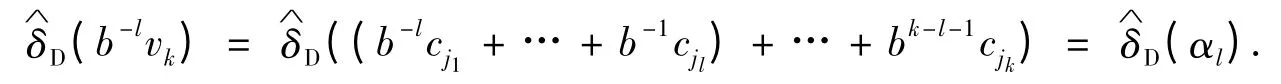
由引理2 知

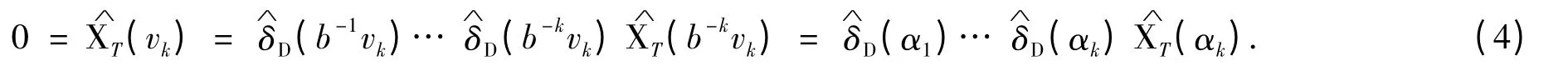
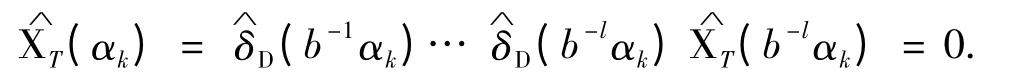
再证充分性.设存在紧集N 使得∀a ∈N，PD(e2πia)=0.假设D 不是自相似tile 数字集，则由引理1 知存在整数m ≠0，使得任意，其中只有某个ci=m(1 ≤i ≤n)，其余均为零.定义无穷路径，其中αk=b－kcj1+…+b－1cjk且α0=0.由紧集的定义知，至少存在一点αl∈N，因此PD(e2πiαl)=0，矛盾.于是充分性得证.

［1］HUTCHINSON J E.Fractals and self-similarity［J］.Indiana Univ Math，1981，30(5):713-747.

［2］董新汉，童继稀.可数无穷迭代函数系的分离性质［J］.湖南师范大学自然科学学报，2011，34(2):1-6.

［3］LAGARIAS J C，WANG Y.Self-affine tiles in Rn［J］.Adv Math，1996，121(1):21-49.

［4］BANDT C.Self-similar sets 5:Integer matrices and fractal tilings of Rn［J］.Proc Amer Math Soc，1991，112(2):549-562.

［5］KENYON R.Self-replicating tilings［C］//Walters P.Symbolic dynamics and its applications［M］.Rhode Island:American Mathematical Society，1992:239-263.

［6］ODLYZKO A M.Non-negative digit sets in positional number systems［J］.Proc London Math Soc，1978，37(3):213-229.

［7］LAGARIAS J C，WANG Y.Integral self-affine tiles in Rn:Ⅰ.Standard and non-standard digits sets［J］.J London Math Soc，1996，54(1):161-179.

［8］LAU K S，RAO H.On one-dimensional self-similar tilings and pq-tiles［J］.Trans Am Math Soc，2002，355(4):1401-1414.

［9］HE X G，LAU K S.Characterization of tile digit sets with prime determinants［J］.Appl Comput Harmon Anal，2004，16(3):159-173.

［10］PROTASOV V.A complete solution characterizing smooth refinable functions［J］.SIAM J Math Anal，2000，31(6):1332-1350.

［11］KENYON R.Projecting the one-dimensional Sierpinski gasket［J］.Israel J Math，1997，97(1):221-238.

［12］LAGARIAS J C，WANG Y.Integral self-affine tiles in Rn:Ⅱ.Lattice tilings［J］.J Fourier Anal Appl，1997，3(1):84-102.