功率VDMOS器件的新型SPICE模型
2013-12-22朱荣霞马德军王锦春孙伟锋张春伟
朱荣霞 黄 栋 马德军 王锦春 孙伟锋 张春伟
(1东南大学国家专用集成电路系统工程技术研究中心,南京 210096)
(2中国空空导弹研究院红外探测器技术航空科技重点实验室,洛阳471009)
垂直双扩散金属氧化物场效应晶体管 (VDMOS器件)是新一代的电力电子开关器件.由于具有独特的高输入阻抗、低驱动功率、优越的频率特性及低噪声等优点[1-3],VDMOS器件成为当前半导体分立器件中的高端产品,应用范围广,市场需求大,发展前景好.目前,VDMOS器件主要应用于电机调速、逆变器、电子开关及汽车电器等领域[4-5].而SPICE模型是连接半导体器件物理与电路的桥梁,VDMOS器件的广泛应用使得人们对其SPICE模型的需求越来越大.
针对VDMOS器件的SPICE模型,Sanchez等[6]初步建立了一种包含准饱和效应的模型,但是该模型没有考虑积累区电阻寄生结型场效应晶体管(JFET)的沟道夹断对于器件特性的影响.Victory等[7]建立了一种基于表面势的VDMOS模型,但该模型仅考虑了寄生JFET沟道未夹断的情况,且对漂移区电阻的计算并不精确.Chauhan等[8]将VDMOS器件看成一个普通的N沟道金属氧化物半导体(NMOS)串联一个受栅压和漏压控制的电阻,该电阻仅仅由一个没有物理意义的经验公式给出,因此,该模型无法准确描述外界电压的变化对VDMOS器件内部特性造成的改变.鉴于已有VDMOS模型精确度差等问题,至今为止,没有一个标准的SPICE模型可以描述VDMOS器件的特性.
本文在经典的MOS模型——BSIM3v3模型的基础上,建立了一套新的描述VDMOS器件电学特性的SPICE模型.为了准确描述VDMOS器件的电学特性,除了考虑外部节点栅极、源极、漏极之外,还增加了4个内部节点,并将VDMOS器件视为1个普通NMOS与4个电阻的串联.
1 VDMOS器件结构及SPICE模型
VDMOS器件通常采用多元胞并联的结构,以增大通态电流.图1为VDMOS器件的元胞结构图.图中,Lt为器件积累区的长度.可以看出,VDMOS器件沿栅漏轴线对称.如图1所示,本文模型在源极(S)、栅极(G)、漏极(D)3个外部节点的基础上又增加了4个内部节点,并分别将节点3与节点4、节点4与漏极D之间的区域定义为C区和E区.不同的区域对于VDMOS器件电学特性的影响是不同的.如图2所示,可将VDMOS器件视为1个普通NMOS器件与4个电阻R1,R2,R3,R4的串联.可将VDMOS器件的源极、栅极及节点1视为1个普通的NMOS器件.栅极电压的变化可使积累区产生的电荷出现积累和耗尽2种状态,故节点1,2之间的区域对于VDMOS器件的影响可被视为1个积累区电阻R1.2个P+体区与N-外延层组成1个寄生JFET结构,随源极、节点2与节点3电压的变化,寄生JFET结构的沟道耗尽或夹断,故在节点2,3之间引入了寄生JFET电阻R2.考虑到VDMOS器件的电流路径在C区与E区是不同的[7],故将这2个区域的电阻分别用R3和R4表示.只需要建立这4个电阻的模型,便可得到VDMOS器件的SPICE模型.
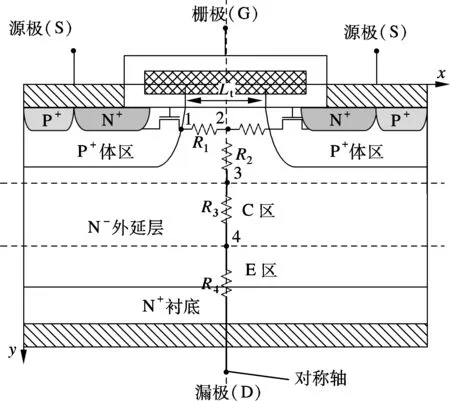
图1 VDMOS器件的元胞剖面图
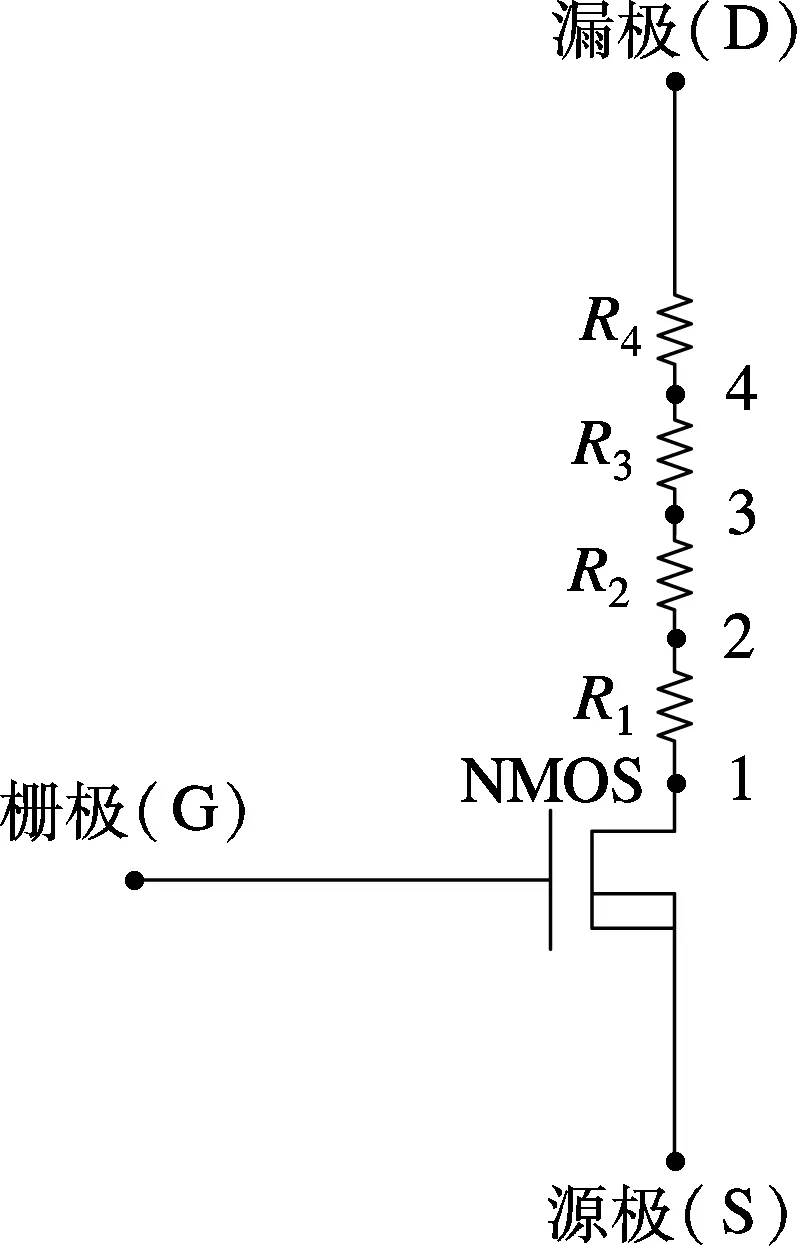
图2 VDMOS器件的SPICE模型结构图
2 模型建立
2.1 积累区电阻R1
2.1.1 电流模型
在VDMOS器件内部,沿x轴方向流过积累区的电流为
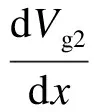
(1)
式中,W为器件的宽度;μN-eff为积累区的有效迁移率;Vg2为器件在积累区内的准费米势;QN-为积累区内载流子的电荷,由积累区杂质电离引入的自由电子和栅极感应电荷Qin两个部分组成,即
QN-=Qin-qNN-tsi
(2)
式中,q为电子电荷;NN-,tsi分别为积累区的掺杂浓度及厚度.
将式(2)代入式(1),沿x轴从节点1到节点2对式(1)进行积分可得[9]
(3)
式中,V1,V2分别为节点1与节点2的电压;V21=V2-V1.由式(3)可以看出,只要计算出Qin所在的积分项,就可以得出积累区的电流.
栅氧及积累区组成的结构类似于一个N阱-P沟道金属氧化物半导体(PMOS)结构.通过解泊松方程,得到积累区的栅极感应电荷Qin为[10]

(4)
式中,Cox为单位面积的栅氧化层电容;γG2为与工艺相关的体效应系数;ψs为积累区的表面电势;φt为热电压.当ψs>0时,积累区表面积累电子,Qin<0;反之,积累区表面耗尽或反型,Qin>0.
当积累区处于强反型状态时,本文将Qin视为一个常数Qdep0,即

(5)
式中,Δφt为与热电压相关的参数;φFg为积累区的费米势.
当积累区处于积累状态时,Qin几乎随栅压VG与Vg2的电压差VGg2线性变化.令VFBg2为积累区的平带电压,当积累区处于积累状态时,栅极感应电荷为
Qin(ac)=-Cox(VGg2-VFBg2-Δφt)
(6)
为了使用统一的公式来描述积累区处于积累状态和强反型状态时栅极感应电荷与VGg2的关系,引入了表面等效电荷Qina[11],即
Qina=-Cox(VGg2q-VFBg2-Δφt)
(7)
VGg2q=VGg2min+0.5[VGg2-Δ-VGb2min+

(8)
式中,VGg2q为VGg2的有效值;Δ为与工艺相关的参数;VGg2min为Qina=Qdep0时VGg2q的值.因此
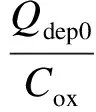
(9)
将式(7)代入式(3)得
(10)

(11)
式中,V21q=VG2q-VG1q.
2.1.2 迁移率模型
VDMOS器件在积累区的迁移率受横向、纵向电场影响.在一定范围内,横向电场越强,积累区自由电子的速度越快;但当横向电场过强时,积累区自由电子的速度则会达到饱和.纵向电场越强,积累区自由电子的运动越趋近于积累区表面,有效迁移率越低.迁移率的经验模型为
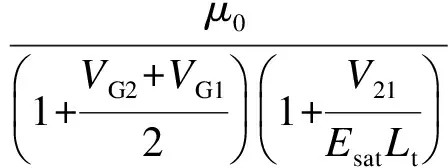
(12)
式中,μ0为不考虑横向、纵向电场影响时的迁移率;Esat为载流子速度饱和时的横向电场.
将式(11)和(12)代入式(10),即可得出完整的积累区电流,进而可由R1=V21/I21得到积累区的等效电阻.
2.2 寄生JFET电阻R2
假设P+体区与N-外延层组成的寄生JFET的沟道(N-外延层)是线性缓变掺杂的,且其组成的PN结为单边突变PN结.图3为寄生JFET电阻及C区、E区电阻的示意图.图中,寄生JFET耗尽层的厚度为Xh(y),其沟道的半壁厚度为b(y)=Lt/2-Xh(y);L为寄生JFET的沟道长度;α≈45°为C区电流路径与y轴的夹角[7];Wt为器件的长度;Wj为节点2到P+体区下边界的厚度;Wc为节点3和节点4之间区域的宽度;Le为节点2到N-外延层底部的厚度;LV为节点2到N+衬底底部的厚度;W1为PN结产生的耗尽层的厚度.节点3所在的垂直于y轴的虚线表示电压为V3的等势线.
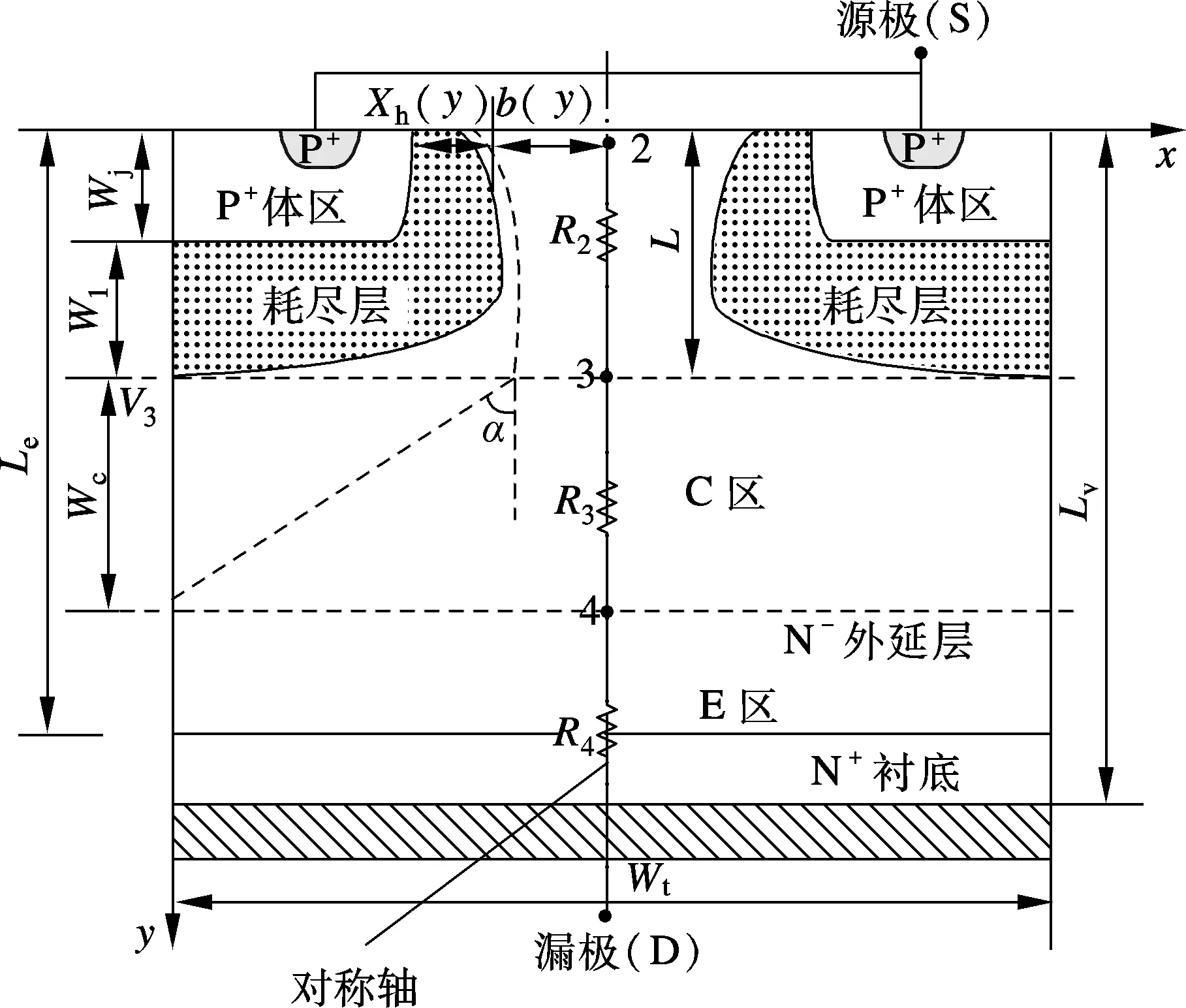
图3 寄生JFET电阻及C区、E区的电阻示意图
寄生JFET沟道的耗尽层厚度为
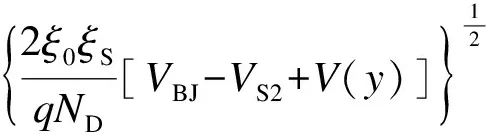
(13)
式中,ξ0为真空介电常数;ξS为硅材料的介电常数;ND为N-外延层的掺杂浓度;V(y)为以节点2为参考点的沟道电势;VBJ为PN结的接触势垒高度;VS2为源极电压VS与V2之间的电压差,即VS2=VS-V2.
2.2.1 线性区电流模型
根据欧姆定律,得到寄生JFET的沟道电流密度为
(14)
式中,μn为寄生JFET沟道的多数载流子迁移率.
考虑到该寄生JFET为对称栅结构,则寄生JFET的沟道总电流为
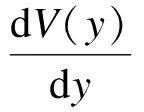
(15)
将电流IC沿沟道从y=0积分到y=L,即可得到肖克莱理论公式.将其简化得到JFET在线性区的电流方程为
(16)
式中,工艺参数β=ξ0ξSμn/Lt;VT为阈值电压;V32为节点3与节点2之间的电压差,即V32=V3-V2.
2.2.2 饱和区电流模型
当V32增加到寄生JFET的沟道夹断电压V32sat时,寄生JFET的沟道开始夹断.随着V32的增大,夹断点到节点2区域内(导电沟道区)的压差始终为V32sat,夹断点向节点2移动,电压降V32-V32sat落在沟道夹断区,进入导电沟道区的载流子将受沟道夹断区电场的作用而漂移到节点3.因此,夹断区的漏极电流仍由导电沟道区的漂移电流决定.
当V32=V32sat时,I32lin的值即为饱和电流I32sat.将V32sat=VS2-VT替换式(16)中的V32得
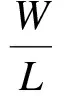
(17)
为考虑沟道长度调制效应,引入沟道调制系数λ=(ΔLV32)/L,其中ΔL为寄生JFET沟道夹断区的长度,则修正后的饱和电流为
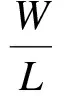
(18)
为使寄生JFET线性区电流与饱和区电流连续,引入节点2与节点3之间的有效电压V32eff[12],即
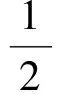
(19)
式中,δ为V32eff的修正参数.
最终得到寄生JFET区的电流方程为
(20)
同样,可由R2=V32/I32得到寄生JFET电阻.
2.3 C区电阻R3及E区电阻R4
在VDMOS器件的C区,由式(13)可得,该处由PN结产生的耗尽层的厚度为

(21)
C区的电阻由耗尽区的边界决定,根据Victory等[7]提出的方法可以得到电阻R3为
(22)
式中,ρ为N-漂移区的电阻率;η为参数.
在E区,电流路径的横截面保持不变,因此该区域的电阻R4只与节点3,4之间区域的宽度Wc有关.本文忽略漏端金属的电阻,则电阻R4可表示为

(23)

(24)
式中,ρN为N+衬底的电阻率.
3 模型验证
本文采用关态击穿电压为625 V的VDMOS器件来验证所建立的模型.图4给出了在提模软件MBP中,使用本文所建模型对VDMOS器件提模得到的拟合结果.由图可知,该VDMOS器件的准饱和效应严重,同时,基于本文模型得到的仿真值可以精确地拟合器件的准饱和区、饱和区及线性区.因此,本文提出的建模思路及方法是有效的.

图4 仿真值与测试值的拟合结果
4 结语
本文建立了功率VDMOS器件的SPICE模型.在VDMOS器件源极、漏极、栅极3个外部节点的基础上又增加4个内部节点,分段考虑了各个节点之间器件的结构特征.通过将VDMOS器件视为1个普通NMOS与4个电阻的串联,准确有效地计算这4个电阻的阻值,建立了精确的VDMOS器件 的SPICE模型.经验证,该模型具有高的精确度,可以准确地拟合VDMOS器件线性区、饱和区、准饱和区的电学特性.
)
[1]Zhang Long,Yu Huilin,Wu Yifan,et al.On state output characteristics and transconductance analysis of high voltage (600V) SJ-VDMOS[C]//Proceedingsof2012IEEEInternationalConferenceonSolid-StateandIntegrated-CircuitTechnology.Xi’an,China,2012: 1-3.
[2]Messaadi Lotfi,Smail Toufik.The electro-thermal sub circuit model for power MOSFETs[J].MicroelectronicsandSolidStateElectronics,2012,1(2): 26-32.
[3]Duan Baoxing,Yang Yintang.Power VDMOS transistor with the step oxide trench breaks the limit line of silicon[J].Micro&NanoLetters,2011,6(9):777-780.
[4]Bao Jiaming,Qi Haochen,Zhang Jian,et al.VDMOS modeling for IC CAD[C]//Proceedingsof2011IEEEJointInternationalInformationTechnologyandArtificialIntelligenceConference.Chongqing,China,2011: 245-249.
[5]Antonios Bazigos,Francoins Krummenacher,Jean Michel Sallese,et al.A physics-based analytical compact model for the drift region of the HV-MOSFET[J].IEEETransactionsonElectronDevices,2011,58(6): 1710-1721.
[6]Sanchez J L,Gharbi M,Tranduce H,et al.Quasisaturation effect in high-voltage VDMOS transistor[J].Solid-StateandElectronDevices,1985,132(1): 42-46.
[7]Victory J J,Sanchez J L,Demassa T A,et al.A static,physical VDMOS model based on the charge-sheet model[J].IEEETransactionsonElectronDevices,1996,43(1): 157-164.
[8]Chauhan Y S,Anghel C,Krummenacher F,et al.A compact DC and AC model for circuit simulation of high voltage VDMOS transistor[C]//Proceedingsofthe7thInternationalSymposiumonQualityElectronicDesign.San Jose,CA,USA,2006:109-114.
[9]Jia Kan,Sun Weifeng,Shi Longxing.A novel surface potential-based short channel MOSFET model for circuit simulation[J].MicroelectronicsJournal,2011,42(10): 1169-1175.
[10]Tsividis Yannis.OperationandmodelingoftheMOStransistor[M].New York: McGraw-Hill,1999.
[11]Shi Longxing,Jia Kan,Sun Weifeng.A novel compact high-voltage LDMOS transistor model for circuit simulation[J].ElectronDevices,2013,60(1): 346-353.
[12]Liu William.MOSFETmodelsforSPICEsimulation,includingBSIM3v3andBSIM4[M].New York: Wiley,2001.
