基于多物理场耦合的混凝土湿热变形数值模拟

陈德鹏

(安徽工业大学建筑工程学院,马鞍山 243002)

(江苏省建筑科学研究院有限公司高性能土木工程材料国家重点实验室,南京 210008)

混凝土材料自身的变形性能有其湿、热变化本质并存在耦合作用[1-2],对于研究混凝土结构的变形开裂及耐久性至关重要．混凝土的体积变化难免会造成混凝土及其结构的变形开裂,使混凝土的渗透性大幅增加,混凝土的碳化、化学侵蚀、钢筋锈蚀等耐久性能劣化过程更容易进行,对混凝土耐久性极为不利[3-4]．混凝土是一种典型的多孔介质,将多孔介质的传热传质原理应用于混凝土湿热耦合传输及变形数值模拟计算,已成为混凝土研究的主要热点之一[5-8]．可用于混凝土湿热耦合数值模拟分析的方法有以下4种:① 基于多孔介质热、质迁移的唯象热力学方法;② 以Luikov传热传质耦合方程为基础的数值分析方法;③ 有限元分析方法;④ 多物理场耦合分析软件．热流唯象方程同时考虑了热流驱动力与质流驱动力的影响,而质流唯象方程只考虑了质流驱动力的作用,没有涉及热流驱动力对质流作用的交叉项,因而,未能全面揭示热、质交叉效应．因受试验条件和许多材料参数的影响,唯象学分析方法难以在实际中应用[9]．以Luikov传热传质耦合方程为基础的数值分析方法,主要用于多孔介质的传热传质分析,但在求解温湿度耦合过程中可能会出现如下问题:① 由于存在很难计算的复杂特征值而得不到结果;② 在控制方程和边界条件同时耦合时无能无力;③ 准确性欠佳，难以反映出多孔介质内的温湿度分布．用传递函数对耦合传输进行求解的方法则相对可行[10],但该解析法要求的条件较严格,传递函数的选择较难,尤其是对于研究环境温湿度条件变化情况下的混凝土内部温湿度分布及由此导致的混凝土变形,已很难利用传递函数进行求解．此外,主流的商业有限元软件还难以直接计算出混凝土中的湿度应力及变形．近年来出现的多物理场耦合模拟计算软件,易于将不同物理场耦合起来进行模拟,已逐渐得到广泛应用．其中,基于偏微分方程对科学和工程问题进行建模和仿真计算的交互开发环境系统COMSOL Multiphysics已在多个领域发挥重要作用．

本文利用COMSOL软件对混凝土湿热耦合变形进行数值模拟,并结合算例,与实际实验结果和解析-有限元结合解法(A-FEM)结果进行比较,以探讨利用COMSOL软件进行湿热耦合甚至湿-热-力耦合作用下水泥基复合材料内部温湿度场、应力场及耦合变形行为的数值模拟的可行性和有效性．

1 多物理场基本模型

利用COMSOL Multiphysics软件对水泥基复合的湿热传输和耦合变形行为进行模拟计算时,物理过程数学模型与解析-有限元结合解法中的湿热耦合传输模型不同,有关解析-有限元结合解法的相关内容详见文献[11]．

1.1 湿扩散模型

通常,假定多孔水泥基材料中的湿传输为扩散形式,且湿度梯度是湿度(液态水和水蒸气)的驱动力,根据Fick定律和质量守恒方程,对于一维传输有如下方程[2]:

(1)

式中,M为湿含量;Dm为湿扩散系数,实际计算时,应对湿扩散系数进行修正,即用考虑Knudsen扩散影响的混凝土湿扩散系数Dmk替换Dm,Dmk=Dmkf,kf为Knudsen扩散影响系数[2];Qm为湿源或湿汇．

1.2 热传输模型

通常采用Fourier定律来描述水泥基材料中的热传输,导热系数则是已经考虑了内部对流等影响的表观导热系数(或称名义导热系数),则一维情况下热传输模型可表示为

(2)

式中,Q为热源或热汇,是由水泥水化放热或其他非传热过程引起的热量变化;T为温度;ρ为水泥基材料表观密度;cp为水泥基材料的比热;λ为水泥基材料的名义导热系数．

1.3 力学平衡方程

假定不同因素引起的混凝土的应力均作用于材料整体,考虑到湿度孔隙压力和热应力，本构关系可以简化为混凝土总应变(εall)与不同因素引起的应变之间的关系,即

εall=εe+εt+εsh

(3)

式中,εe为外荷载引起的弹性应变;εt为热应变;εsh为干缩应变．

温度变形可以根据温度场利用混凝土材料的线性热膨胀系数直接得到,而湿度分布引起的湿度变形很难如温度的变形效应一样直接进行处理．本文使用湿膨胀系数来解决湿度分布难以进行变形计算的难题,并使得湿度变形计算像温度变形计算一样简单．模仿热膨胀系数,将湿膨胀系数定义为材料内部单位湿度变化所导致的体积变化或长度变化．

2 基于COMSOL的多物理场耦合模拟计算

瑞典COMSOL公司开发的COMSOL Multiphysics是一款大型的高级数值仿真软件,因其高效的计算性能和杰出的多场直接耦合分析能力,被广泛应用于各个领域的科学研究以及工程计算[12]．在交互环境下,对于基于偏微分方程组的多物理耦合过程,COMSOL不再需要编制复杂的偏微分方程组的求解器,而是利用其内嵌的多种物理模型如化学反应工程模型、热传导模型、结构力学模型等．偏微分方程组模式是其功能最强大、最灵活的求解方法,有3个数学应用模式描述偏微分方程组:系数形式(coefficient form)、通式(general form) 和弱形式(weak form)．通常,通式模式适宜求解非线性问题,已足够解决大部分多物理场耦合问题．本文围绕混凝土中温湿度场和湿热耦合变形的湿-热-力三场耦合问题,综合采用通式微分方程组(描述热传导方程和湿扩散方程)和结构力学模型进行模拟计算．

确定物理场模型后,可利用GUI界面进行模型选择和尺寸、参数定义等,然后进行网格划分、定义边界条件等,从而可运行COMSOL进行计算．COMSOL在求解过程中,首先把结构力学模型和通式微分方程组结合起来进行转换,转变为统一的通式形式的微分方程组,然后进行求解得到温度场、湿度场和位移场,实现三场的耦合求解．利用COMSOL分析多物理场耦合问题,可以避免一些松散耦合解法求解多物理场问题的误差,实现了多物理场的过程耦合,得出的物理过程的数值解答更加准确[13]．COMSOL的求解结果可以用等势线、曲线、云图及动画等多种方式来表达．

3 算例分析

试验数据取自Hundt开展的长达3年的混凝土变形试验,6个混凝土试件的尺寸均为2.4 m×0.4 m×0.4 m[14];另外,利用解析-有限元结合解法对Hundt试验情况进行数值模拟得到的结果,也作为对比数据．在解析-有限元结合解法求解中,首先将湿热耦合传输偏微分方程、边界条件和初始条件进行Laplace变换,再利用传递函数将耦合方程组转变为比较容易求解的四阶偏微分方程,然后在Laplace域中进行求解,最后再对Laplace域中求解结果进行Laplace逆变换,就可得到时间和空间上的温湿度分布．根据温湿度分布的解析结果,湿度分布还需要首先进行应力转化过程,然后通过有限单元法计算混凝土在温湿度耦合作用下的变形及规律[11]．

Hundt试验的试验条件如图1所示,试件侧表面(不含端面)经处理成为绝热绝湿状态保证其一维扩散,试件一端密封置于80 ℃的温度环境中,另一端不作密封处理置于To=20 ℃、RH=45%的环境中.试件成型后对混凝土试件不同位置的温度进行了测定,并继续对经28 d标准养护后的混凝土试件进行湿度分布及变形测试．图中，M0为试件内部初始湿含量，T0为内部初始温度.

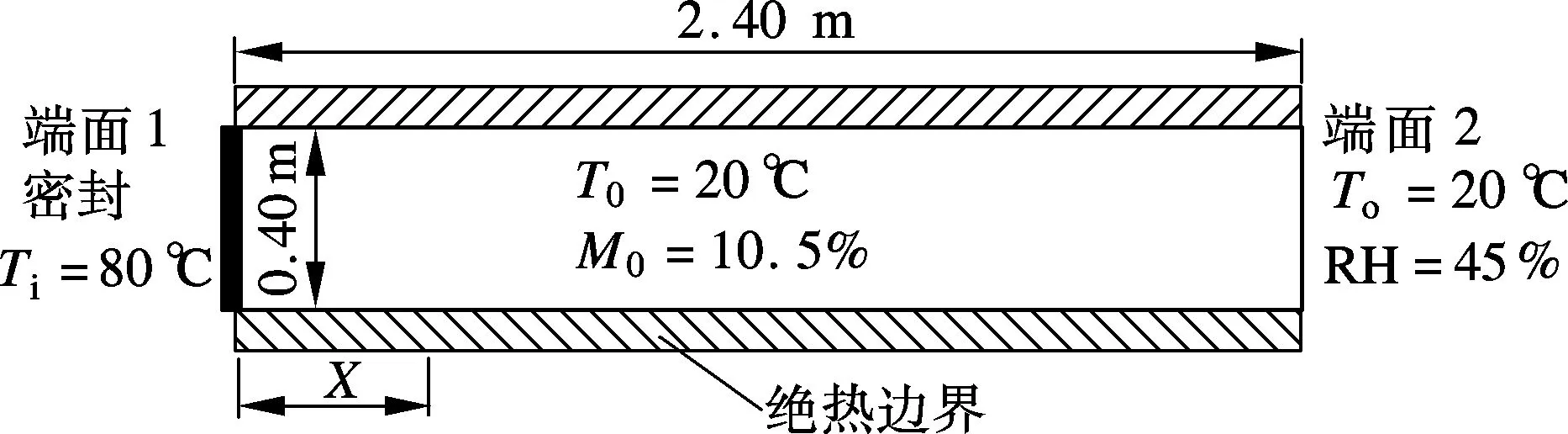
图1 Hundt试验试件及边界条件示意图

基于多物理场耦合利用COMSOL进行模拟计算与利用解析-有限元结合解法进行计算分析中需要用到的混凝土参数见表1．数值模拟计算结果与试验结果见图2和图3．

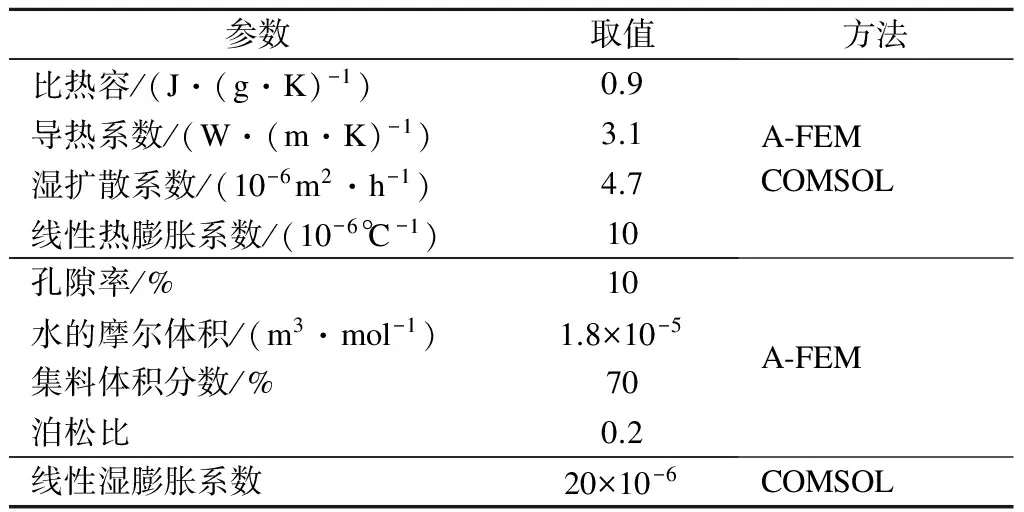
表1 混凝土湿热耦合变形计算所需参数

图2 混凝土试件长度变化

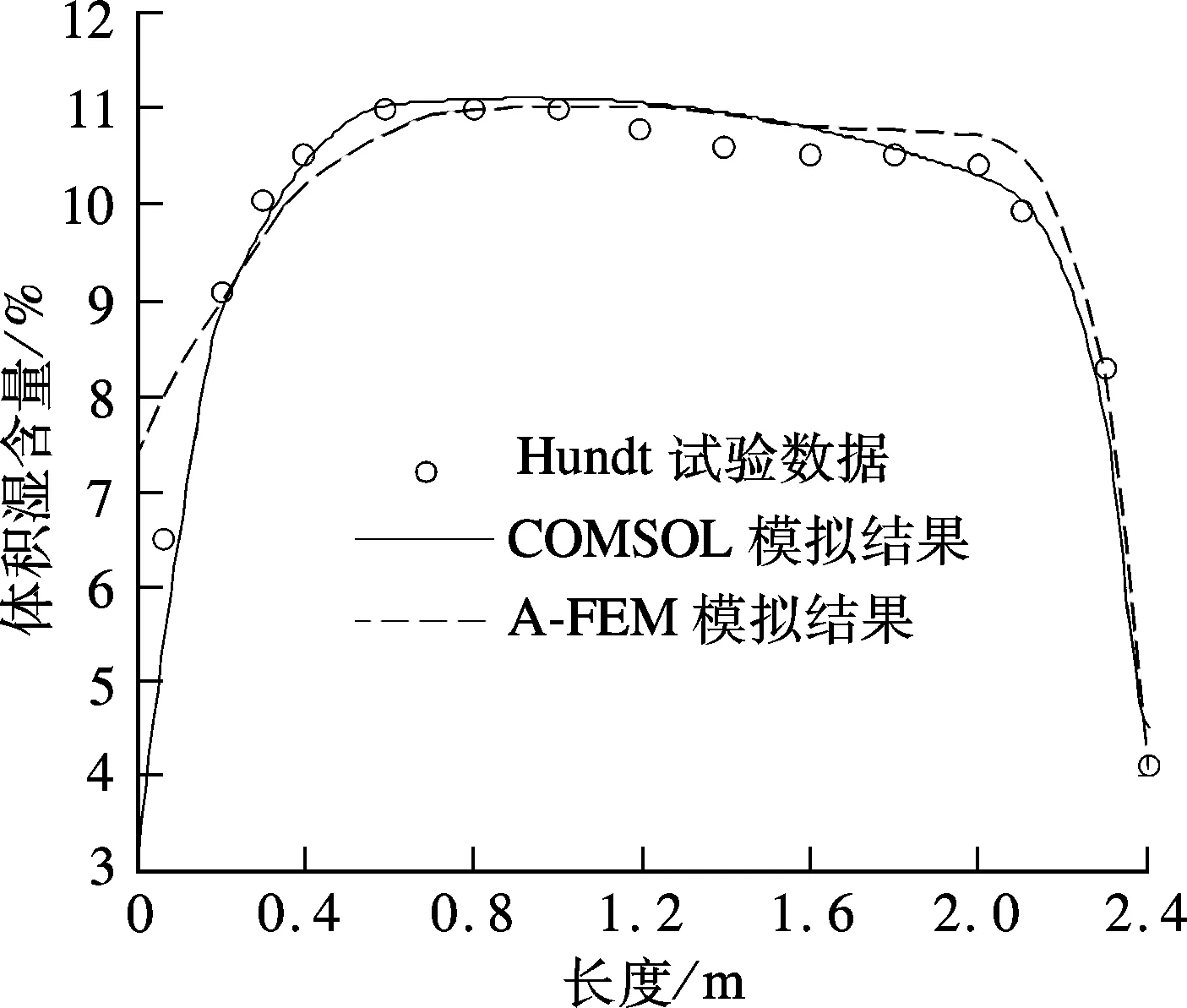
图3 混凝土内部湿含量(550 d时)

从图2和图3可看出,混凝土试件长度和含湿量的数值模拟结果与试验值符合很好,说明通过该方法对混凝土材料及结构进行变形模拟分析是可行的．图3中曲线的形状可从以下2个方面进行解释:① 受端部环境湿度影响,混凝土内部湿流向端面2扩散;② 由于附近高温环境的影响,密封端湿流向端面2方向迁移．因此,试件中部混凝土饱和后的湿含量比初始时还要高．

4 工程应用实例分析

某浅埋湖底隧道采用放坡明挖法施工,大开挖后隧道主体结构采用现浇混凝土跳仓法施工,每隔60 m设置竖向变形缝,竖向变形缝间混凝土跳仓施工段内设置3个施工缝，形成长度为15 m的4个施工段,施工段内按底板-中隔墙-侧墙-顶板的顺序进行混凝土浇注．利用本文提出的基于COMSOL多物理场耦合数值模拟方法对隧道侧墙混凝土的变形进行模拟计算,数值模拟结果与主体结构侧墙某伸缩缝处位移的光纤光栅监测结果、解析-有限元结合解法计算结果进行比较．

4.1 数值模拟分析建模

根据混凝土材料及跳仓施工的特点,计算中采用如下假定:① 混凝土为多孔介质且内部均匀连续,因此初始温湿度分布均匀;② 钢筋混凝土的比热、导热系数等热物参数可利用改进的加权平均方法由混凝土、钢筋自身参数值进行推定[15];③ 墙板内不同长度上的温湿度在距表面相同深度处的大小相同;④ 径向混凝土板两端自由伸缩;⑤ 因关注隧道服役期间的混凝土变形,故忽略水泥水化热的热变形效应;⑥ 模拟计算自成型后60 d始,根据同配比混凝土室内试验及现场测试，受水泥水化影响的混凝土变形平均值取为230×10-6．

根据隧道主体结构施工时的竖向施工缝和分层施工高度,取15 m×1 m×3 m的墙板作为分析对象,如图4所示．

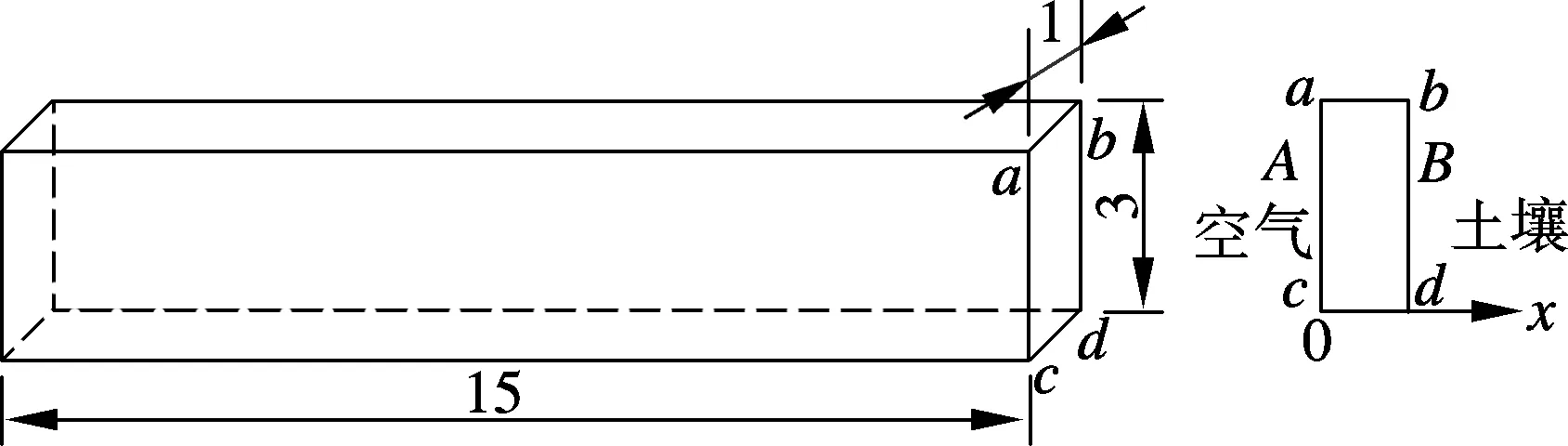
图4 混凝土墙板尺寸示意图(单位：m)

在隧道结构内侧(x=0),假定空气与混凝土直接接触(建设期内),空气中温湿度将对混凝土内部温度和湿度产生影响,应属于第三类边界条件．实际模拟分析中,环境温度和湿度此时应属于温湿度函数在结构边界上已知的情况,见图5．实际计算中,每天的温湿度分布由实验值通过插值得到．

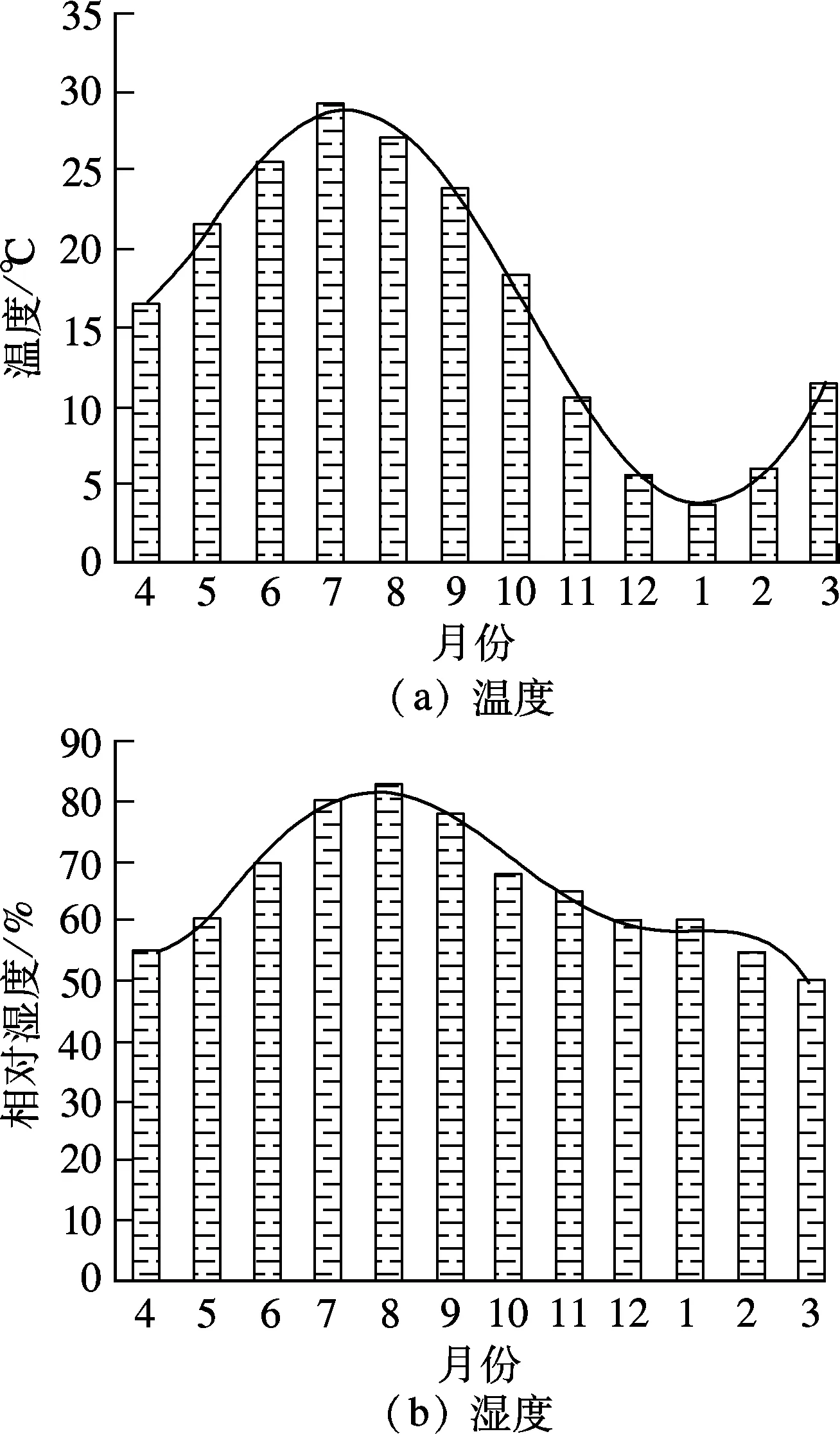
图5 隧道内部年度月平均温湿度

在隧道外侧(x=l),自防水结构混凝土和外包防水层的综合效果较好,可认为无水分交换,且由于隧道侧墙混凝土在一定深度湖底的土层中温度相对恒定,因此可假定为绝湿绝热边界．

混凝土中初始温度和湿度认为是均匀分布的,根据测定,隧道主体结构混凝土初始温度为12 ℃,初始湿度为3.5%(对应于RH=95%)[8]．

4.2 模拟计算结果及分析

在实际应用算例的模拟计算中,所用到的混凝土基本湿热物参数与利用解析-有限单元结合解法相同[11],由于采用了“线性湿膨胀系数”,原解析-有限元结合解法中的变形相关参数无需再使用,见表2．

4.2.1 温湿度分布

利用基于多物理场耦合的混凝土湿热耦合变形模拟方法和解析-有限元结合解法对某隧道混凝土墙板进行模拟计算，得到的内部温湿度分布情况见图6．图中，“x/l=0.4”表示距离内侧表面相对深度为0.4处的位置．

从图6可看出,在隧道内侧为时变环境边界条件、外侧为绝热绝湿条件的情况下,混凝土内部温湿度分布的变化滞后于实际环境温湿度的变化,且随距混凝土表面深度的不同而存在差异．距离内表面越近,试件内温湿度的波动幅度也越大;而隧道外侧混凝土内的温湿度变化波动较小．湿度和温度变化曲线的发展趋势相反．图6(b)中，240 d时较大的湿度变化应与此时期内混凝土内部水分因环境温度较高而蒸发比较活跃有关．

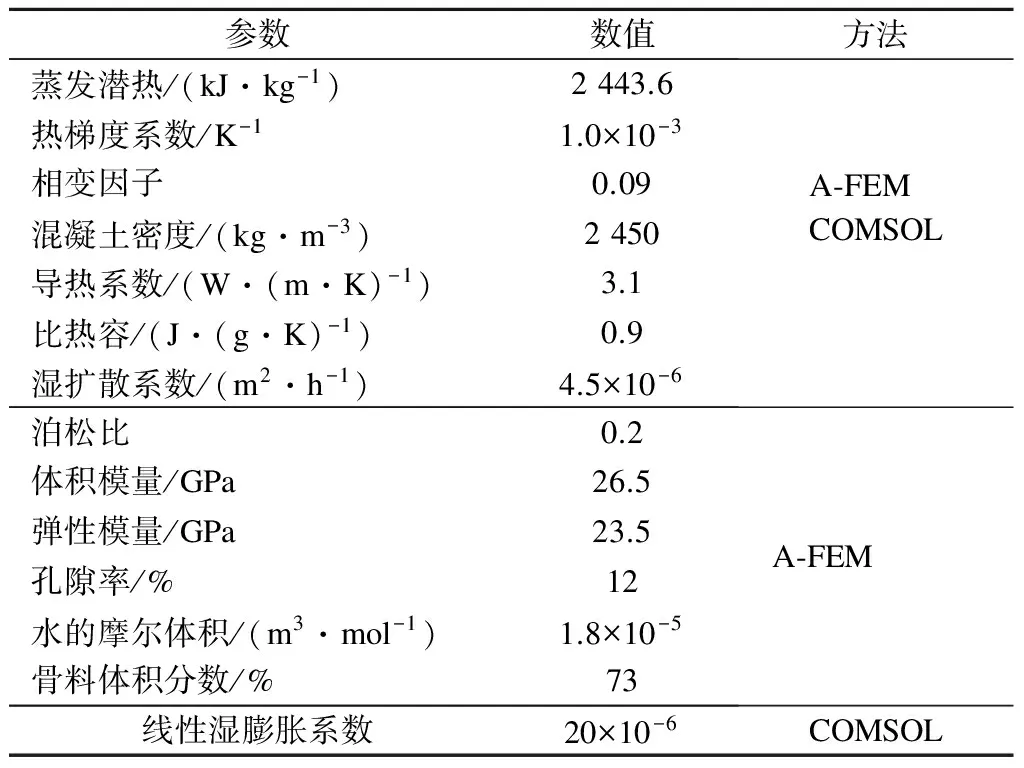
表2 数值模拟中所用的混凝土参数

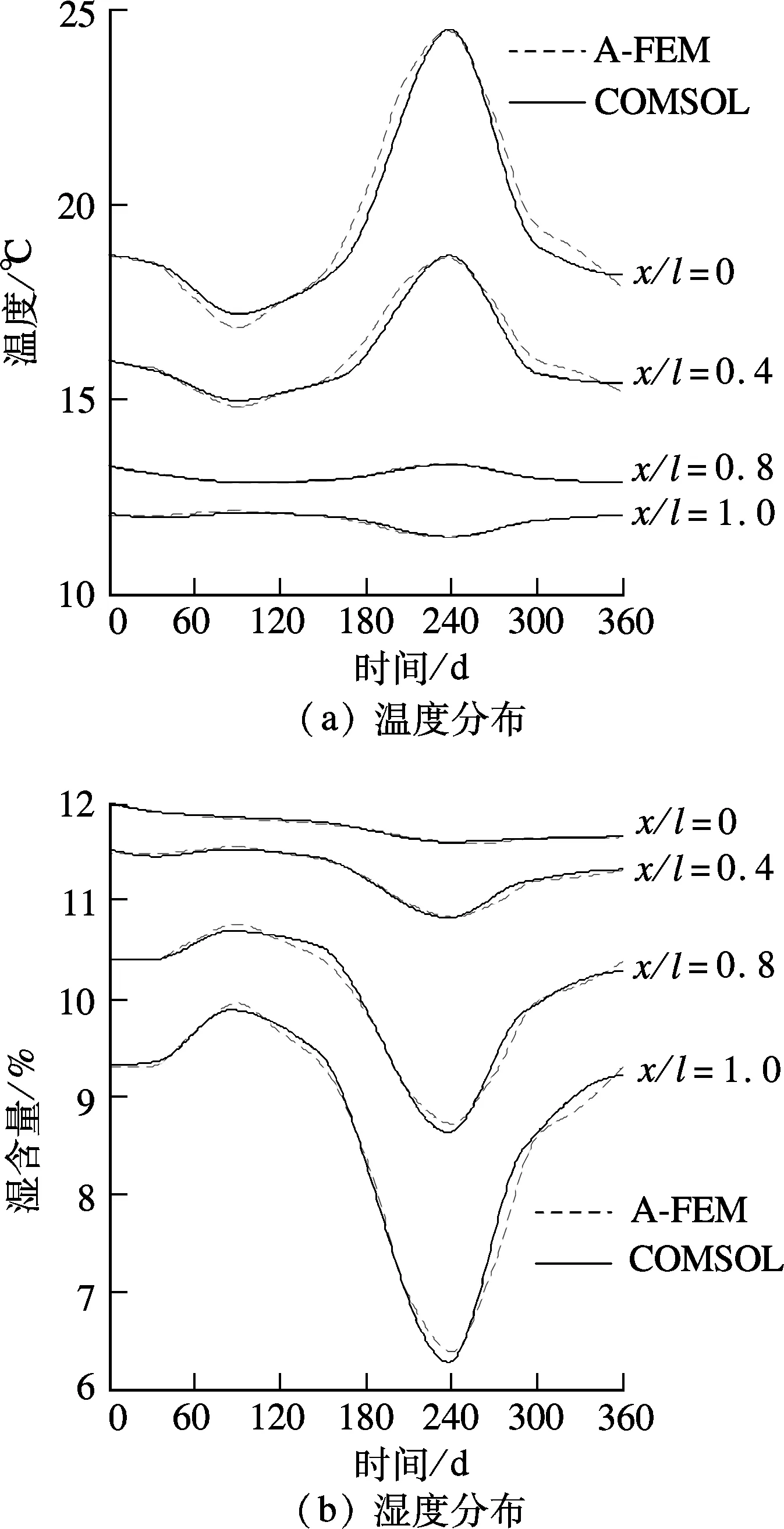
图6 混凝土内部温湿度模拟计算结果

4.2.2 湿热耦合变形

COMSOL法和解析-有限元结合解法的湿热耦合变形结果如图7所示．

由图7可见,距离隧道内表面较远时,混凝土内部温湿度变化对环境温湿度变化不敏感．与环境温湿度的波动相比,混凝土变形的变化存在滞后性,这符合导热性差的混凝土的热胀冷缩特点．

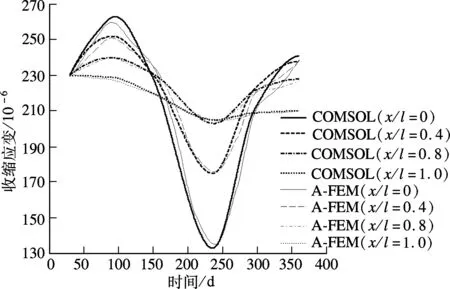
图7 混凝土湿热耦合变形的COMSOL数值模拟结果

4.2.3 横向伸缩缝位移

为了与光纤光栅监测结果(伸缩缝位移)进行比较,首先将COMSOL和A-FEM模拟的应变结果乘以伸缩缝间墙体长度得到伸缩缝间墙体变形值．

由图8可知,混凝土变形的COMSOL数值模拟结果比解析-有限元结合解法结果更加接近光纤光栅实测结果,变形发展规律与光纤光栅监测结果基本一致,较准确地反映了混凝土在真实结构中的变形发展情况．

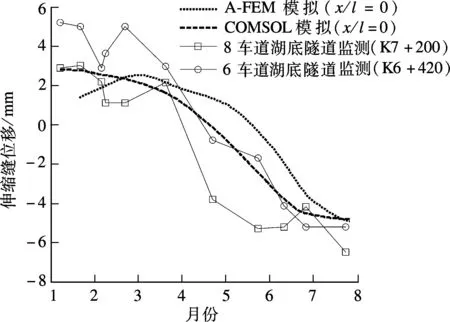
图8 光纤光栅监测结果与数值模拟结果比较

5 结论

1) 根据混凝土的多孔介质特点,基于多物理场耦合和多孔介质湿热传输原理提出了可利用COMSOL进行计算的湿-热-力多物理场模型．经算例和工程实例模拟计算证实了多物理场模型的正确性和COMSOL软件进行混凝土耦合变形计算的可行性．

2) 本文中的算例及工程实际应用实例的结果表明,基于多物理场耦合利用COMSOL计算混凝土内部温湿度分布、应力及变形比利用解析-有限元结合解法进行求解更加方便,模拟计算结果也更加准确．

)

[1]Shoukry S N,William G W,Downie B,et al.Effect of moisture and temperature on the mechanical properties of concrete[J].ConstructionandBuildingMaterials,2011,25(2): 688-696.

[2]陈德鹏.基于多孔介质湿热传输理论的混凝土湿热耦合变形数值模拟及应用[D].南京: 东南大学材料科学与工程学院,2007.

[3]Mehta P K.Durability—critical issues for the future[J].ConcreteInternational,1997,19(7): 27-32.

[4]Hossain K M A,Lachemi M.Strength,durability and micro-structural aspects of high performance volcanic ash concrete[J].CementandConcreteResearch,2007,37(5): 759-766.

[5]De Borst R.Challenges in computational materials science: multiple scales,multi-physics and evolving discontinuities[J].ComputationalMaterialsScience,2008,43(1): 1-15.

[6]Bazant Z P,Yu Q,Li G H,et al.Modeling of creep and hygrothermal deformations of concrete: intriguing consequences of nano-porosity[C]//TheFourthBiotConferenceonPoromechanics.Columbia,USA,2009: 3-16.

[7]Tariku F,Kumaran K,Fazio P.Transient model for coupled heat,air and moisture transfer through multilayered porous media[J].InternationalJournalofHeatandMassTransfer,2011,53(15/16): 3035-3044.

[8]Sykora J,Sejnoha M,Sejnoha J.Homogenization of coupled heat and moisture transport in masonry structures including interfaces[J].AppliedMathematicsandComputation,2013,219(13): 7275-7285.

[9]Jensen O M,Hansen P F.Autogenous deformation and RH-change in perspective[J].CementandConcreteResearch,2001,31(12): 1859-1865.

[10]Chang W J,Weng C I.Analytical solution to coupled heat and moisture diffusion transfer in porous materials[J].InternationalJournalofHeatandMassTransfer,2000,43(19): 3621-3632.

[11]Chen D,Qian C,Liu C.A numerical simulation approach to calculating hygrothermal deformation of concrete based on heat and moisture transfer in porous medium[J].InternationalJournalofCivilEngineering,2010,8(4): 287-296.

[12]CnTech.COMSOL Multiphysics全球第一款真正的多物理场耦合分析软件 [EB/OL].(2008-09-05)[2012-02-01].http://www.cntech.com.cn/newsflash/2008/comsol.html.

[13]盛金昌.多孔介质流-固-热三场全耦合数学模型及数值模拟[J].岩石力学与工程学报,2006,25(S1): 3028-3033.

Sheng Jinchang.Fully coupled thermo-hydro-mechanical model of saturated porous media and numerical modelling[J].ChineseJournalofRockMechanicsandEngineering,2006,25(S1):3028-3033.(in Chinese)

[14]Hundt J.Wärme-und feuchtigkeit leitung in beton unter einwirkung eines temperaturfälles,technical report 256 [R].Berlin: Deutscher Ausschuß für Stahlbeton,1975.

[15]陈德鹏,钱春香,王辉,等.水泥基材料比热容测定及计算方法的研究[J].建筑材料学报,2007,10(2): 127-131.

Chen Depeng,Qian Chunxiang,Wang Hui,et al.Research on determination and calculation method of specific heat capacity of cement-based materials [J].JournalofBuildingMaterials,2007,10(2): 127-131.(in Chinese)